Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-09T23:28:08.795Z Has data issue: false hasContentIssue false
  • English
  • Français

One-dimensional system arising in stochastic gradient descent

Part of: Limit theorems Numerical methods in calculus of variations and optimal control

Published online by Cambridge University Press:  01 July 2021

Konstantinos Karatapanis
Konstantinos Karatapanis*
Affiliation:
University of Pennsylvania
*
*Postal address: University of Pennsylvania, Department of Mathematics, 209 South 33rd Street, United States. Email address: kkarat@sas.upenn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider stochastic differential equations of the form 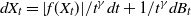$dX_t = |f(X_t)|/t^{\gamma} dt+1/t^{\gamma} dB_t$, where f(x) behaves comparably to 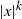$|x|^k$ in a neighborhood of the origin, for 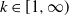$k\in [1,\infty)$. We show that there exists a threshold value 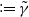$ \,{:}\,{\raise-1.5pt{=}}\, \tilde{\gamma}$ for 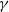$\gamma$, depending on k, such that if 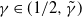$\gamma \in (1/2, \tilde{\gamma})$, then 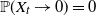$\mathbb{P}(X_t\rightarrow 0) = 0$, and for the rest of the permissible values of 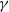$\gamma$, 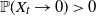$\mathbb{P}(X_t\rightarrow 0)>0$. These results extend to discrete processes that satisfy 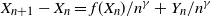$X_{n+1}-X_n = f(X_n)/n^\gamma +Y_n/n^\gamma$. Here, 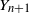$Y_{n+1}$ are martingale differences that are almost surely bounded.

This result shows that for a function F whose second derivative at degenerate saddle points is of polynomial order, it is always possible to escape saddle points via the iteration 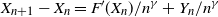$X_{n+1}-X_n =F'(X_n)/n^\gamma +Y_n/n^\gamma$ for a suitable choice of 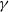$\gamma$.

Keywords

Stochastic approximationsgradient descentsaddle pointsstochastic differential equations

MSC classification

Primary: 60F15: Strong theorems
Secondary: 49M15: Newton-type methods
Type
Original Article
Information
Advances in Applied Probability , Volume 53 , Issue 2 , June 2021 , pp. 575 - 607
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agarwal, N. et al. (2017). Finding approximate local minima faster than gradient descent. In Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, Association for Computing Machinery, New York, pp. 1195–1199.Google Scholar
Anandkumar, A. and Ge, R. (2016). Efficient approaches for escaping higher order saddle points in non-convex optimization. In Proceedings of the 29th Annual Conference on Learning Theory (Proceedings of Machine Learning Research 49), PMLR, New York, pp. 81–102.Google Scholar
Brennan, R. W. and Rogers, P. (1995). Stochastic optimization applied to a manufacturing system operation problem. In Proceedings of the 27th Conference on Winter Simulation, IEEE Computer Society, Washington, DC, pp. 857–864.Google Scholar
Chen, X., Lee, J. D., Tong, X. T. and Zhang, Y. (2016). Statistical inference for model parameters in stochastic gradient descent. Ann. Statist. 48, 251–273.Google Scholar
Choromanska, A. et al. (2015). The loss surfaces of multilayer networks. J. Mach. Learn. Res. 38, 192–204.Google Scholar
Daneshmand, H., Kohler, J., Lucchi, A. and Hofmann, T. (2018). Escaping saddles with stochastic gradients. In Proceedings of the 35th International Conference on Machine Learning (Proceedings of Machine Learning Research 80), PMLR, Stockholm, pp. 1155–1164.Google Scholar
Durrett, R. (2013). Probability: Theory and Examples. Duxbury Press, Belmont, CA.Google Scholar
Even-Dar, E. and Mansour, Y. (2001). Learning rates for q-learning. J. Mach. Learn. Res. 5, 1–25, 2001.Google Scholar
Fisher, E. (1992). On the law of the iterated logarithm for martingales. Ann. Prob. 20, 675–680.CrossRefGoogle Scholar
Ge, R., Huang, F., Jin, C. and Yuan, Y. (2015). Escaping from saddle points: online stochastic gradient for tensor decomposition. In Proceedings of the 28th Conference on Learning Theory (Proceedings of Machine Learning Research 40), PMLR, Paris, pp. 797–842.Google Scholar
Gelfand, S. B. and Mitter, S. K. (1991). Recursive stochastic algorithms for global optimization in $\mathbb{R}^d $. SIAM J. Control Optimization 29, 999–1018.CrossRefGoogle Scholar
Hill, B. M., D., Lane and Sudderth, W. (1980). A strong law for some generalized urn processes. Ann. Prob. 8, 214–226.CrossRefGoogle Scholar
Jin, C. et al. (2017). How to escape saddle points efficiently. Preprint. Available at http://arxiv.org/abs/1703.00887.Google Scholar
Jain, P., Jin, C., Kakade, S. M. and Netrapalli, P. (2015). Computing matrix squareroot via non convex local search. Preprint. Available at http://arxiv.org/abs/1507.05854.Google Scholar
Kushner, H. and Yin, G. G. (2003). Stochastic Approximation and Recursive Algorithms and Applications. Springer, New York.Google Scholar
Li, T., Liu, L., Kyrillidis, A. and Caramanis, C. (2018). Statistical inference using SGD. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence (AAAI-18), AAAI Press, Palo Alto, CA, pp. 3571–3578.Google Scholar
Lee, J. D., Simchowitz, M., Jordan, M. I. and Recht, B. (2016). Gradient descent converges to minimizers. Preprint. Available at http://arxiv.org/abs/1602.04915.Google Scholar
Lojasiewicz inequality. Encyclopedia of Mathematics. Website, accessed 15 September 2019. Available at https://www.encyclopediaofmath.org/index.php/Lojasiewicz_inequality.Google Scholar
Pemantle, R. (1990). Nonconvergence to unstable points in urn models and stochastic approximations. Ann. Prob. 18, 698–712.CrossRefGoogle Scholar
Pemantle, R. (1991). When are touchpoints limits for generalized Pólya urns? Proc. Amer. Math. Soc. 113, 235–243.Google Scholar
Pemantle, R. (2007). A survey of random processes with reinforcement. Prob. Surveys 4, 1–79.CrossRefGoogle Scholar
Polyak, B. T. and Juditsky, A. B. (1992). Acceleration of stochastic approximation by averaging. SIAM J. Control Optimization 30, 838–855.CrossRefGoogle Scholar
Robbins, H. and Monro, S. (1951). A stochastic approximation method. Ann. Math. Statist. 22, 400–407.CrossRefGoogle Scholar
Raginsky, M., Rakhlin, A. and Telgarsky, M. (2017). Non-convex learning via Stochastic Gradient Langevin Dynamics: a nonasymptotic analysis. Preprint. Available at http://arxiv.org/abs/1702.03849.Google Scholar
Rakhlin, A., Shamir, O. and Sridharan, K. (2012). Making gradient descent optimal for strongly convex stochastic optimization. In Proceedings of the 29th International Conference on Machine Learning, Omnipress, pp. 1571–1578.Google Scholar
Ruppert, D. (1988). Efficient estimations from a slowly convergent Robbins-Monro process. Tech. Rep., Cornell University Operations Research and Industrial Engineering.Google Scholar
Rogers, L. C. G. and Williams, D. (1987). Diffusions, Markov Processes and Martingales, Vol. 2: Itô Calculus. John Wiley, New York.Google Scholar
Suri, R. and Leung, Y. T. (1987). Single run optimization of a SIMAN model for closed loop flexible assembly systems. In Proceedings of the 19th Conference on Winter Simulation, Association for Computing Machinery, New York, pp. 738–748.Google Scholar
Sun, R. and Luo, Z. Q. (2016). Guaranteed matrix completion via non-convex factorization. IEEE Trans. Inf. Theory 62, 6535–6579.CrossRefGoogle Scholar
Son, P. T. (2012). An explicit bound for the Łojasiewicz exponent of real polynomials. Kodai Math. J. 35, 311–319.Google Scholar
Sun, J., Qu, Q. and Wright, J. (2017). Complete dictionary recovery over the sphere I: overview and the geometric picture. IEEE Trans. Inf. Theory 63, 853–884.CrossRefGoogle Scholar