Consider the problem of determining the Bayesian credibility mean 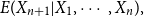$E(X_{n+1}|X_1,\cdots, X_n),$ whenever the random claims 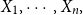$X_1,\cdots, X_n,$ given parameter vector 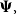$\boldsymbol{\Psi},$ are sampled from the K-component mixture family of distributions, whose members are the union of different families of distributions. This article begins by deriving a recursive formula for such a Bayesian credibility mean. Moreover, under the assumption that using additional information 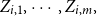$Z_{i,1},\cdots,Z_{i,m},$ one may probabilistically determine a random claim 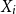$X_i$ belongs to a given population (or a distribution), the above recursive formula simplifies to an exact Bayesian credibility mean whenever all components of the mixture distribution belong to the exponential families of distributions. For a situation where a 2-component mixture family of distributions is an appropriate choice for data modelling, using the logistic regression model, it shows that: how one may employ such additional information to derive the Bayesian credibility model, say Logistic Regression Credibility model, for a finite mixture of distributions. A comparison between the Logistic Regression Credibility (LRC) model and its competitor, the Regression Tree Credibility (RTC) model, has been given. More precisely, it shows that under the squared error loss function, it shows the LRC’s risk function dominates the RTC’s risk function at least in an interval which about 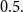$0.5.$ Several examples have been given to illustrate the practical application of our findings.