Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-05-30T04:25:40.229Z Has data issue: false hasContentIssue false
  • English
  • Français

DISTANCE GEOMETRY IN QUASIHYPERMETRIC SPACES. I

Part of: Distance geometry Other generalizations

Published online by Cambridge University Press:  19 June 2009

PETER NICKOLAS  and
REINHARD WOLF
PETER NICKOLAS*
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, Wollongong, NSW 2522, Australia (email: peter_nickolas@uow.edu.au)
REINHARD WOLF
Affiliation:
Institut für Mathematik, Universität Salzburg, Hellbrunnerstrasse 34, A-5020 Salzburg, Austria (email: Reinhard.Wolf@sbg.ac.at)
*
✉For correspondence; e-mail: peter˙nickolas@uow.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X,d) be a compact metric space and let ℳ(X) denote the space of all finite signed Borel measures on X. Define I:ℳ(X)→ℝ by 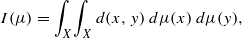and set M(X)=sup I(μ), where μ ranges over the collection of signed measures in ℳ(X) of total mass 1. The metric space (X,d) is quasihypermetric if for all n∈ℕ, all α1,…,αn∈ℝ satisfying ∑ i=1nαi=0 and all x1,…,xn∈X, the inequality ∑ i,j=1nαiαjd(xi,xj)≤0 holds. Without the quasihypermetric property M(X) is infinite, while with the property a natural semi-inner product structure becomes available on ℳ0(X), the subspace of ℳ(X) of all measures of total mass 0. This paper explores: operators and functionals which provide natural links between the metric structure of (X,d), the semi-inner product space structure of ℳ0(X) and the Banach space C(X) of continuous real-valued functions on X; conditions equivalent to the quasihypermetric property; the topological properties of ℳ0(X) with the topology induced by the semi-inner product, and especially the relation of this topology to the weak-* topology and the measure-norm topology on ℳ0(X); and the functional-analytic properties of ℳ0(X) as a semi-inner product space, including the question of its completeness. A later paper [P. Nickolas and R. Wolf, Distance geometry in quasihypermetric spaces. II, Math. Nachr., accepted] will apply the work of this paper to a detailed analysis of the constant M(X).

Keywords

compact metric spacefinite metric spacequasihypermetric spacemetric embeddingsigned measuresigned measure of mass zerospaces of measuresdistance geometrygeometric constant

MSC classification

Secondary: 51K05: General theory 31C45: Other generalizations (nonlinear potential theory, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 80 , Issue 1 , August 2009 , pp. 1 - 25
Copyright
Copyright © Australian Mathematical Society 2009

Footnotes

The authors are grateful for the financial support and hospitality of the University of Salzburg and the Centre for Pure Mathematics in the School of Mathematics and Applied Statistics at the University of Wollongong.

References

[1] Alexander, R., ‘Generalized sums of distances’, Pacific J. Math. 56 (1975), 297–304.CrossRefGoogle Scholar
[2] Alexander, R., ‘Two notes on metric geometry’, Proc. Amer. Math. Soc. 64 (1977), 317–320.Google Scholar
[3] Alexander, R., ‘Geometric methods in the study of irregularities of distribution’, Combinatorica 10 (1990), 115–136.CrossRefGoogle Scholar
[4] Alexander, R., ‘Principles of a new method in the study of irregularities of distribution’, Invent. Math. 103 (1991), 279–296.CrossRefGoogle Scholar
[5] Alexander, R. and Stolarsky, K. B., ‘Extremal problems of distance geometry related to energy integrals’, Trans. Amer. Math. Soc. 193 (1974), 1–31.CrossRefGoogle Scholar
[6] Björck, G., ‘Distributions of positive mass, which maximize a certain generalized energy integral’, Ark. Mat. 3 (1956), 255–269.Google Scholar
[7] Blumenthal, L. M., Theory and Applications of Distance Geometry, 2nd edn (Chelsea Publishing Co., New York, 1970).Google Scholar
[8] Bourbaki, N., Éléments de mathématique. Fasc. XIII. Livre VI: Intégration. Chapitres 1, 2, 3 et 4, 2nd revised and extended edn, Actualités Scientifiques et Industrielles, No. 1175 (Hermann, Paris, 1965).Google Scholar
[9] Bretagnolle, J., Dacunha-Castelle, D. and Krivine, J.-L., ‘Lois stables et espaces L p’, Ann. Inst. H. Poincaré Sect. B (N.S.) 2 (1965/1966), 231–259.Google Scholar
[10] Choquet, G., Lectures on Analysis. Vol. I: Integration and Topological Vector Spaces (eds. J. Marsden, T. Lance and S. Gelbart) (W. A. Benjamin, Inc., New York, Amsterdam, 1969).Google Scholar
[11] Cleary, J., Morris, S. A. and Yost, D., ‘Numerical geometry – numbers for shapes’, Amer. Math. Monthly 93 (1986), 260–275.CrossRefGoogle Scholar
[12] Danzer, L. and Grünbaum, B., ‘Über zwei Probleme bezüglich konvexer Körper von P. Erdős und von V. L. Klee’, Math. Z. 79 (1962), 95–99.CrossRefGoogle Scholar
[13] Dor, L. E., ‘Potentials and isometric embeddings in L 1’, Israel J. Math. 24 (1976), 260–268.Google Scholar
[14] Farkas, B. and Révész, S. G., ‘Rendezvous numbers in normed spaces’, Bull. Aust. Math. Soc. 72 (2005), 423–440.CrossRefGoogle Scholar
[15] Farkas, B. and Révész, S. G., ‘Rendezvous numbers of metric spaces – a potential theoretic approach’, Arch. Math. (Basel) 86 (2006), 268–281.Google Scholar
[16] Fuglede, B., ‘On the theory of potentials in locally compact spaces’, Acta Math. 103 (1960), 139–215.CrossRefGoogle Scholar
[17] Gross, O., ‘The Rendezvous value of a metric space’, in: Advances in Game Theory (Princeton University Press, Princeton, NJ, 1964), pp. 49–53.Google Scholar
[18] Herz, C. S., ‘A class of negative-definite functions’, Proc. Amer. Math. Soc. 14 (1963), 670–676.CrossRefGoogle Scholar
[19] Hinrichs, A., ‘Averaging distances in finite-dimensional normed spaces and John’s ellipsoid’, Proc. Amer. Math. Soc. 130 (2002), 579–584 (electronic).CrossRefGoogle Scholar
[20] Kelly, J. B., ‘Hypermetric spaces and metric transforms’, in: Inequalities, III (Proc. Third Sympos., Univ. California, Los Angeles, Calif., 1969; dedicated to the memory of Theodore S. Motzkin) (Academic Press, New York, 1972), pp. 149–158.Google Scholar
[21] Kelly, J. B., ‘Hypermetric spaces’, in: The Geometry of Metric and Linear Spaces (Proc. Conf., Michigan State Univ., East Lansing, Mich., 1974), Lecture Notes in Mathematics, 490 (Springer, Berlin, 1975), pp. 17–31.CrossRefGoogle Scholar
[22] Landkof, N. S., Foundations of Modern Potential Theory (Springer, New York, 1972), Translated from the Russian by A. P. Doohovskoy, Grundlehren der mathematischen Wissenschaften, Band 180.CrossRefGoogle Scholar
[23] Larcher, G., Schmid, W. C. and Wolf, R., ‘On the approximation of certain mass distributions appearing in distance geometry’, Acta Math. Hungar. 87 (2000), 295–316.CrossRefGoogle Scholar
[24] Lévy, P., Théorie de l’addition des variables aléatoires (Gauthier-Villars, Paris, 1937).Google Scholar
[25] Lovász, L., Pyber, L., Welsh, D. J. A. and Ziegler, G. M., Combinatorics in Pure Mathematics, Handbook of combinatorics, 1, 2 (Elsevier, Amsterdam, 1995), pp. 2039–2082.Google Scholar
[26] Morris, S. A. and Nickolas, P., ‘On the average distance property of compact connected metric spaces’, Arch. Math. (Basel) 40 (1983), 459–463.CrossRefGoogle Scholar
[27] Nickolas, P. and Wolf, R., Distance geometry in quasihypermetric spaces. II, Math. Nachr. accepted.Google Scholar
[28] Nickolas, P. and Wolf, R., Distance geometry in quasihypermetric spaces. III. Submitted.Google Scholar
[29] Powell, M. J. D., The Theory of Radial Basis Function Approximation in 1990, Advances in Numerical Analysis, Vol. II (Lancaster, 1990) (Oxford University Press, New York, 1992), pp. 105–210.Google Scholar
[30] Schoenberg, I. J., ‘On certain metric spaces arising from Euclidean spaces by a change of metric and their imbedding in Hilbert space’, Ann. of Math. (2) 38 (1937), 787–793.CrossRefGoogle Scholar
[31] Schoenberg, I. J., ‘Metric spaces and positive definite functions’, Trans. Amer. Math. Soc. 44 (1938), 522–536.CrossRefGoogle Scholar
[32] Stadje, W., ‘A property of compact connected spaces’, Arch. Math. (Basel) 36 (1981), 275–280.Google Scholar
[33] Taylor, A. E. and Lay, D. C., Introduction to Functional Analysis, 2nd edn (Krieger, Melbourne, FL, 1986).Google Scholar
[34] Wolf, R., ‘Averaging distances in certain Banach spaces’, Bull. Aust. Math. Soc. 55 (1997), 147–160.CrossRefGoogle Scholar
[35] Wolf, R., ‘On the average distance property and certain energy integrals’, Ark. Mat. 35 (1997), 387–400.CrossRefGoogle Scholar
[36] Wolf, R., ‘Averaging distances in real quasihypermetric Banach spaces of finite dimension’, Israel J. Math. 110 (1999), 125–151.CrossRefGoogle Scholar
[37] Yost, D., ‘Average distances in compact connected spaces’, Bull. Aust. Math. Soc. 26 (1982), 331–342.CrossRefGoogle Scholar