Let 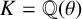$K={\mathbb {Q}}(\theta )$ be an algebraic number field with 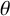$\theta $ satisfying a monic irreducible polynomial 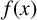$f(x)$ of degree n over 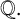${\mathbb {Q}}.$ The polynomial 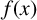$f(x)$ is said to be monogenic if $\{1,\theta ,\ldots ,\theta ^{n-1}\}$ is an integral basis of K. Deciding whether or not a monic irreducible polynomial is monogenic is an important problem in algebraic number theory. In an attempt to answer this problem for a certain family of polynomials, Jones [‘A brief note on some infinite families of monogenic polynomials’, Bull. Aust. Math. Soc. 100 (2019), 239–244] conjectured that if 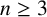$n\ge 3$, 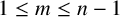$1\le m\le n-1$, 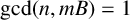$\gcd (n,mB)=1$ and A is a prime number, then the polynomial 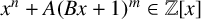$x^n+A (Bx+1)^m\in {\mathbb {Z}}[x]$ is monogenic if and only if 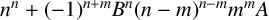$n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA$ is square-free. We prove that this conjecture is true.