Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-06-08T12:37:38.064Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantitative inverse theorem for Gowers uniformity norms 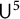$\mathsf {U}^5$ and 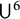$\mathsf {U}^6$ in 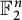$\mathbb {F}_2^n$

Part of: Additive number theory; partitions Algebraic combinatorics

Published online by Cambridge University Press:  15 June 2023

Luka Milićević Open the ORCID record for Luka Milićević [Opens in a new window]
Luka Milićević*
Affiliation:
Mathematical Institute of the Serbian Academy of Sciences and Arts, Belgrade, Serbia
*
e-mail: luka.milicevic@turing.mi.sanu.ac.rs
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove quantitative bounds for the inverse theorem for Gowers uniformity norms 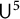$\mathsf {U}^5$ and 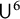$\mathsf {U}^6$ in 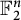$\mathbb {F}_2^n$. The proof starts from an earlier partial result of Gowers and the author which reduces the inverse problem to a study of algebraic properties of certain multilinear forms. The bulk of the work in this paper is a study of the relationship between the natural actions of 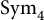$\operatorname {Sym}_4$ and 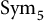$\operatorname {Sym}_5$ on the space of multilinear forms and the partition rank, using an algebraic version of regularity method. Along the way, we give a positive answer to a conjecture of Tidor about approximately symmetric multilinear forms in five variables, which is known to be false in the case of four variables. Finally, we discuss the possible generalization of the argument for 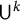$\mathsf {U}^k$ norms.

Keywords

Gowers uniformity normsmultilinear formssymmetric groupspartition rankinverse theorems

MSC classification

Primary: 11P70: Inverse problems of additive number theory, including sumsets 05E18: Group actions on combinatorial structures
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 50
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the Serbian Ministry of Science, Technological Development and Innovation through the Mathematical Institute of the Serbian Academy of Sciences and Arts.

References

Austin, T., Partial difference equations over compact Abelian groups, I: modules of solutions. Preprint, 2014. arXiv:1305.7269 Google Scholar
Austin, T., Partial difference equations over compact Abelian groups, II: step-polynomial solutions. Preprint, 2014. arXiv:1309.3577 Google Scholar
Bergelson, V., Tao, T., and Ziegler, T., An inverse theorem for the uniformity seminorms associated with the action of ${F}_p^{\infty }$ . Geom. Funct. Anal. 19(2010), 1539–1596. https://doi.org/10.1007/s00039-010-0051-1 CrossRefGoogle Scholar
Bhowmick, A. and Lovett, S., Bias vs structure of polynomials in large fields, and applications in effective algebraic geometry and coding theory. IEEE Trans. Inform. Theory 69(2022), 963–977. https://doi.org/10.1109/TIT.2022.3214372 CrossRefGoogle Scholar
Camarena, O. A. and Szegedy, B., Nilspaces, nilmanifolds and their morphisms. Preprint, 2012. arXiv:1009.3825 Google Scholar
Candela, P., Notes on nilspaces: algebraic aspects . Discrete Anal. 15(2017), 1–59. https://doi.org/10.19086/da.2105 Google Scholar
Candela, P., Notes on compact nilspaces . Discrete Anal. 16(2017), 1–57. https://doi.org/10.48550/arXiv.1605.08940 Google Scholar
Candela, P., González-Sánchez, D., and Szegedy, B., On higher-order Fourier analysis in characteristic. Ergodic Theory Dynam. Systems, to appear. https://doi.org/10.1017/etds.2022.119 CrossRefGoogle Scholar
Candela, P. and Szegedy, B., Regularity and inverse theorems for uniformity norms on compact abelian groups and nilmanifolds. https://doi.org/10.1515/crelle-2022-0016 CrossRefGoogle Scholar
Candela, P. and Szegedy, B., Nilspace factors for general uniformity seminorms, cubic exchangeability and limits. Mem. Amer. Math. Soc. 287(2023), no. 1425. https://doi.org/10.1090/memo/1425 CrossRefGoogle Scholar
Gowers, W. T., A new proof of Szemerédi’s theorem . Geom. Funct. Anal. 11(2001), 465–588. https://doi.org/10.1007/s00039-001-0332-9 CrossRefGoogle Scholar
Gowers, W. T. and Milićević, L., A quantitative inverse theorem for the ${U}^4$ norm over finite fields. Preprint, 2017. arXiv:1712.00241 Google Scholar
Gowers, W. T. and Milićević, L., An inverse theorem for Freiman multi-homomorphisms. Preprint, 2020. arXiv:2002.11667 Google Scholar
Gowers, W. T. and Milićević, L., A note on extensions of multilinear maps defined on multilinear varieties . Proc. Edinb. Math. Soc. (2) 64(2021), no. 2, 148–173. https://doi.org/10.1017/s0013091521000055 CrossRefGoogle Scholar
Gowers, W. T. and Wolf, J., Linear forms and higher-degree uniformity functions on ${F}_p^n$ . Geom. Funct. Anal. 21(2011), 36–69. https://doi.org/10.1007/s00039-010-0106-3 CrossRefGoogle Scholar
Green, B. and Tao, T., An inverse theorem for the Gowers ${U}^3(G)$ -norm . Proc. Edinb. Math. Soc. (2) 51(2008), 73–153. https://doi.org/10.1017/s0013091505000325 CrossRefGoogle Scholar
Green, B. and Tao, T., The distribution of polynomials over finite fields, with applications to the Gowers norms . Contrib. Discrete Math. 4(2009), no. 2, 1–36. https://doi.org/10.11575/cdm.v4i2.62086 Google Scholar
Green, B. and Tao, T., Linear equations in primes . Ann. of Math. (2) 171(2010), no. 3, 1753–1850. https://doi.org/10.4007/annals.2010.171.1753 CrossRefGoogle Scholar
Green, B., Tao, T., and Ziegler, T., An inverse theorem for the Gowers ${U}^{s+1}[N]$ -norm . Ann. of Math. (2) 176(2012), 1231–1372. https://doi.org/10.4007/annals.2012.176.2.11 CrossRefGoogle Scholar
Gutman, Y., Manners, F., and Varjú, P., The structure theory of Nilspaces II: representation as nilmanifolds . Trans. Amer. Math. Soc. 371(2019), 4951–4992. https://doi.org/10.1090/tran/7503 CrossRefGoogle Scholar
Gutman, Y., Manners, F., and Varjú, P., The structure theory of nilspaces I . J. Anal. Math. 140(2020), 299–369. https://doi.org/10.1007/s11854-020-0093-8 CrossRefGoogle Scholar
Gutman, Y., Manners, F., and Varjú, P., The structure theory of nilspaces III: inverse limit representations and topological dynamics . Adv. Math. 365(2020), 107059. https://doi.org/10.1016/j.aim.2020.107059 CrossRefGoogle Scholar
Jamneshan, A. and Tao, T., The inverse theorem for the ${U}^3$ Gowers uniformity norm on arbitrary finite abelian groups: Fourier-analytic and ergodic approaches. Preprint, 2023. arXiv:2112.13759 Google Scholar
Janzer, O., Polynomial bound for the partition rank vs the analytic rank of tensors . Discrete Anal. 7(2020), 1–18. https://doi.org/10.19086/da.12935 Google Scholar
Manners, F., Quantitative bounds in the inverse theorem for the Gowers ${U}^{s+1}$ -norms over cyclic groups. Preprint, 2018. arXiv:1811.00718 Google Scholar
Milićević, L., Polynomial bound for partition rank in terms of analytic rank . Geom. Funct. Anal. 29(2019), 1503–1530. https://doi.org/10.1007/s00039-019-00505-4 CrossRefGoogle Scholar
Milićević, L., An inverse theorem for certain directional Gowers uniformity norms. Publ. Inst. Math. (Beograd) (N.S.) 113(2023), 1–56. https://doi.org/10.2298/PIM2327001M CrossRefGoogle Scholar
Milićević, L., Approximately symmetric forms far from being exactly symmetric. Combin. Probab. Comput. 32(2023), 299–315. https://doi.org/10.1017/S0963548322000244 CrossRefGoogle Scholar
Naslund, E., The partition rank of a tensor and $k$ -right corners in ${F}_q^n$ . J. Combin. Theory Ser. A 174(2020), 105190. https://doi.org/10.1016/j.jcta.2019.105190 CrossRefGoogle Scholar
Samorodnitsky, A., Low-degree tests at large distances . In: STOC’07—proceedings of the 39th annual ACM symposium on theory of computing, ACM, New York, 2007, pp. 506–515. https://doi.org/10.1145/1250790.1250864 Google Scholar
Sanders, T., On the Bogolyubov–Ruzsa lemma. Anal. PDE 5(2012), no. 3, 627–655. https://doi.org/10.2140/apde.2012.5.627 CrossRefGoogle Scholar
Szegedy, B., On higher order Fourier analysis. Preprint, 2012. arXiv:1203.2260 Google Scholar
Tao, T. and Ziegler, T., The inverse conjecture for the Gowers norm over finite fields in low characteristic . Ann. Comb. 16(2012), 121–188. https://doi.org/10.1007/s00026-011-0124-3 CrossRefGoogle Scholar
Tidor, J., Quantitative bounds for the ${U}^4$ -inverse theorem over low characteristic finite fields. Discrete Anal. 14(2022), 17 pp. https://doi.org/10.19086/da.38591 CrossRefGoogle Scholar