Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-11T08:06:14.800Z Has data issue: false hasContentIssue false
  • English
  • Français

The Isoperimetric Inequality for Curves with Self-Intersections

Published online by Cambridge University Press:  20 November 2018

Andrew Vogt
Andrew Vogt*
Affiliation:
Department of Mathematics, Georgetown University Washington, D.C. 20057, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Banchoff and Pohl [3] have proved the following generalization of the isoperimetric inequality.

Theorem. If γ is a closed, not necessarily simple, planar curve of length L, and w(p) is the winding number of a variable point p with respect to γ, then

1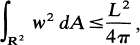

with equality holding if and only if γ is a circle traversed a finite number of times in the same sense.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 24 , Issue 2 , 01 June 1981 , pp. 161 - 167
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Aleksandrov, P. S., Combinatorial Topology, vol. 1, Graylock Press, Rochester, N.Y., 1956 (translation by Horace Komm).Google Scholar
2. Apostol, T. M., Mathematical Analysis, Addison-Wesley, Reading, Mass., 1957.Google Scholar
3. Banchoff, T. F. and Pohl, W. F., A generalization of the isoperimetric inequality, J. Differential Geometry. 6 (1971), 175-192.Google Scholar
4. Courant, R. and Hilbert, D., Methods of Mathematical Physics, vol. 1, Interscience Publishers, Inc., New York, 1953.Google Scholar
5. Fédérer, H., Geometric Measure Theory, Springer-Verlag, Berlin, 1969.Google Scholar
6. Hewitt, E. and Stromberg, K., Real and Abstract Analysis, Springer-Verlag, New York, 1965.Google Scholar
7. Newman, M. H. A., Elements of the Topology of Plane Sets of Points, University Press, Cambridge, England, 1964.Google Scholar
8. Osserman, R., The isoperimetric inequality, Bull. Amer. Math. Soc. 84. 6 (1978), 1182-1238.Google Scholar
9. RadÓ, T., A lemma on the topological index, Fund. Math.. 27 (1936), 212-225.Google Scholar
10. RadÓ, T., The isoperimetric inequality and the Lebesgue definition of surface area, Trans. Amer. Math. Soc.. 41 (1947), 530-555.Google Scholar