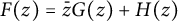1 Introduction and preliminaries
One of the open problems in classical complex analysis is to obtain the precise value of the Bloch constant for analytic functions in the unit disk. In [Reference Chen, Gauthier and Hengartner6], Chen et al. considered the analogous problem of estimating the Bloch constant for planar harmonic mappings. See also the work of Chen and Guathier [Reference Chen and Gauthier5] for planar harmonic and pluriharmonic mappings. Motivated by the work from [Reference Chen, Gauthier and Hengartner6], this topic was dealt by a number of authors with considerable improvements over the previously known Landau-type theorems. These will be indicated later in this section. In this article, we consider bi-analytic and biharmonic mappings and establish several new sharp versions of Landau-type theorems for these two classes of mappings.
1.1 Definitions and notations
A complex-valued function f is a bi-analytic (resp. harmonic) on a domain
![]() $D\subset \mathbb {C}$
if and only if f is twice continuously differentiable and satisfies the bi-analytic equation
$D\subset \mathbb {C}$
if and only if f is twice continuously differentiable and satisfies the bi-analytic equation
![]() $f_{\bar {z}\bar {z}}(z)=0$
(resp. Laplacian equation
$f_{\bar {z}\bar {z}}(z)=0$
(resp. Laplacian equation
![]() $f_{z\overline {z}}(z)=0$
) in D, where we use the common notations for its formal derivatives:
$f_{z\overline {z}}(z)=0$
) in D, where we use the common notations for its formal derivatives:
Note also that
 $$ \begin{align*}\Delta f=4f_{z\overline{z}}=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}. \end{align*} $$
$$ \begin{align*}\Delta f=4f_{z\overline{z}}=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}. \end{align*} $$
It is well-known that every bi-analytic function f in a simply connected domain D has the representation (cf. [Reference Abdulhadi and Hajj1])
where g and h are complex-valued analytic functions in D. Similarly, every harmonic function f in a simply connected domain D can be written as
![]() $f=h+\overline {g}$
with
$f=h+\overline {g}$
with
![]() $f(0)=h(0)$
, where g and h are analytic on D (for details, see [Reference Clunie and Sheil-Small11]).
$f(0)=h(0)$
, where g and h are analytic on D (for details, see [Reference Clunie and Sheil-Small11]).
A complex-valued function F is said to be biharmonic on a domain
![]() $D\subset \mathbb {C}$
if and only if F is four times continuously differentiable and satisfies the biharmonic equation
$D\subset \mathbb {C}$
if and only if F is four times continuously differentiable and satisfies the biharmonic equation
![]() $\Delta (\Delta f)=0$
in D. It is well-known (cf. [Reference Abdulhadi, Muhanna and Khuri3]) that a biharmonic mapping F in a simply connected domain D has the following representation:
$\Delta (\Delta f)=0$
in D. It is well-known (cf. [Reference Abdulhadi, Muhanna and Khuri3]) that a biharmonic mapping F in a simply connected domain D has the following representation:
where G and H are harmonic in D.
A domain
![]() $D\subset \mathbb {C}$
is said to be starlike if and only if the line segment
$D\subset \mathbb {C}$
is said to be starlike if and only if the line segment
![]() $[0,w]$
joining the origin
$[0,w]$
joining the origin
![]() $0$
to every other point
$0$
to every other point
![]() $w\in D$
lies entirely in D.
$w\in D$
lies entirely in D.
Definition 1.1 (cf. [Reference Luo and Ponnusamy23–Reference Ponnusamy and Qiao25])
A continuously differentiable function F on
![]() $\mathbb{D}=\{z: |z|<1\}$
is said to be fully starlike in
$\mathbb{D}=\{z: |z|<1\}$
is said to be fully starlike in
![]() $\mathbb{D}$
if it is sense-preserving,
$\mathbb{D}$
if it is sense-preserving,
![]() $F(0)= 0, F(z)\neq 0$
in
$F(0)= 0, F(z)\neq 0$
in
![]() $\mathbb{D}\backslash \{0\}$
and the curve
$\mathbb{D}\backslash \{0\}$
and the curve
![]() $F(re^{it})$
is starlike with respect to the origin for each
$F(re^{it})$
is starlike with respect to the origin for each
![]() $r\in (0, 1)$
. The last condition is same as saying that
$r\in (0, 1)$
. The last condition is same as saying that
 $$ \begin{align*} \frac{\partial\arg F(re^{it})}{\partial t} =\mathrm{Re}\bigg(\frac{z F_z(z)- \bar{z} F_{\bar z}(z)}{F(z)}\bigg)> 0 \end{align*} $$
$$ \begin{align*} \frac{\partial\arg F(re^{it})}{\partial t} =\mathrm{Re}\bigg(\frac{z F_z(z)- \bar{z} F_{\bar z}(z)}{F(z)}\bigg)> 0 \end{align*} $$
for all
![]() $z = r\, e^{it}$
and
$z = r\, e^{it}$
and
![]() $r\in (0, 1)$
.
$r\in (0, 1)$
.
For a complex-valued function f in D, its Jacobian
![]() $J_f(z)$
is given by
$J_f(z)$
is given by
![]() $J_f(z)=|f_z(z)|^2-|f_{\overline {z}}(z)|^2$
. We say that a harmonic mapping f is locally univalent and sense-preserving if and only if its Jacobian
$J_f(z)=|f_z(z)|^2-|f_{\overline {z}}(z)|^2$
. We say that a harmonic mapping f is locally univalent and sense-preserving if and only if its Jacobian
![]() $J_f(z)>0$
for
$J_f(z)>0$
for
![]() $z\in D$
(cf. [Reference Lewy16]). For continuously differentiable function f, let
$z\in D$
(cf. [Reference Lewy16]). For continuously differentiable function f, let
Throughout,
![]() ${\mathbb D}_{r}=\{z\in \mathbb {C}:\,|z|<r\}$
denotes the open disk about the origin so that
${\mathbb D}_{r}=\{z\in \mathbb {C}:\,|z|<r\}$
denotes the open disk about the origin so that
![]() ${\mathbb D}:= {\mathbb D}_1$
is the unit disk. For the convenience of the reader, let us fix some basic notations.
${\mathbb D}:= {\mathbb D}_1$
is the unit disk. For the convenience of the reader, let us fix some basic notations.
-
•
 $\mathrm {Hol}({\mathbb D})=\{f:\, f \mbox { is analytic in } \mathbb {D}\}$
.
$\mathrm {Hol}({\mathbb D})=\{f:\, f \mbox { is analytic in } \mathbb {D}\}$
. -
•
 $\mathcal {B}_M=\{f \in \mathrm {Hol}({\mathbb D}):\, |f(z)|\leq M ~\mbox { in } {\mathbb D}\}.$
$\mathcal {B}_M=\{f \in \mathrm {Hol}({\mathbb D}):\, |f(z)|\leq M ~\mbox { in } {\mathbb D}\}.$
-
•
 $\mathcal {A}_0=\{f \in \mathrm {Hol}({\mathbb D}):\, f(0) =0\}$
and
$\mathcal {A}_0=\{f \in \mathrm {Hol}({\mathbb D}):\, f(0) =0\}$
and
 $\mathcal {A}_1=\{f \in \mathrm {Hol}({\mathbb D}):\, f'(0) =1\}.$
$\mathcal {A}_1=\{f \in \mathrm {Hol}({\mathbb D}):\, f'(0) =1\}.$
-
•
 $\mathcal {A}=\{f \in \mathrm {Hol}({\mathbb D}):\, f(0) =0=f'(0)-1\}:= \mathcal {A}_1 \cap \mathcal {A}_0.$
$\mathcal {A}=\{f \in \mathrm {Hol}({\mathbb D}):\, f(0) =0=f'(0)-1\}:= \mathcal {A}_1 \cap \mathcal {A}_0.$
-
•
 $\mathcal {H}=\{f:\, f \mbox { is harmonic in } \mathbb {D}\}.$
$\mathcal {H}=\{f:\, f \mbox { is harmonic in } \mathbb {D}\}.$
-
•
 $\mathcal {H}_0=\{f\in \mathcal {H}:\, f(0) =0\}.$
$\mathcal {H}_0=\{f\in \mathcal {H}:\, f(0) =0\}.$
-
•
 $\mathcal {BH}_M=\{f\in \mathcal {H}:\, |f(z)|\leq M ~\mbox { in } {\mathbb D}\}.$
$\mathcal {BH}_M=\{f\in \mathcal {H}:\, |f(z)|\leq M ~\mbox { in } {\mathbb D}\}.$
-
•
 $\mathcal {BH}_M^0= \mathcal {BH}_M\cap \mathcal {H}_0.$
$\mathcal {BH}_M^0= \mathcal {BH}_M\cap \mathcal {H}_0.$
-
•
 $\mathrm {Bi}\mathcal {H}=\{f:\, f \mbox { is biharmonic in } \mathbb {D}\}.$
$\mathrm {Bi}\mathcal {H}=\{f:\, f \mbox { is biharmonic in } \mathbb {D}\}.$
-
•
 $\mathrm {Bi}\mathcal {A}_0=\{f:\, f \mbox { is bi-analytic in } \mathbb {D} \mbox { with } f(0)=0\}.$
$\mathrm {Bi}\mathcal {A}_0=\{f:\, f \mbox { is bi-analytic in } \mathbb {D} \mbox { with } f(0)=0\}.$
Definition 1.2
A function f in a family is said to belong to
![]() ${\mathcal S}(r;R)$
if it is univalent in
${\mathcal S}(r;R)$
if it is univalent in
![]() ${\mathbb D}_r$
and the range
${\mathbb D}_r$
and the range
![]() $f(\mathbb {D}_r)$
contains a schlicht disk
$f(\mathbb {D}_r)$
contains a schlicht disk
![]() $\mathbb {D}_R$
.
$\mathbb {D}_R$
.
1.2 Landau and Bloch theorems
The classical theorem of Landau states that if
![]() $f\in \mathcal {B}_M \cap \mathcal {A}$
for some
$f\in \mathcal {B}_M \cap \mathcal {A}$
for some
![]() $M>1$
, then
$M>1$
, then
![]() $f\in {\mathcal S}(r;R)$
with
$f\in {\mathcal S}(r;R)$
with
![]() $r=1/(M+\sqrt {M^2-1})$
and
$r=1/(M+\sqrt {M^2-1})$
and
![]() $R=Mr^2$
. This result is sharp, with the extremal function
$R=Mr^2$
. This result is sharp, with the extremal function
![]() $f_0(z)=M z \frac {1-Mz}{M-z}$
.
$f_0(z)=M z \frac {1-Mz}{M-z}$
.
The Bloch theorem asserts the existence of a positive constant number b such that if
![]() $f\in \mathcal {A}_1$
, then
$f\in \mathcal {A}_1$
, then
![]() $f({\mathbb D})$
contains a schlicht disk of radius b, that is, a disk of radius b which is the univalent image of some subregion of the unit disk
$f({\mathbb D})$
contains a schlicht disk of radius b, that is, a disk of radius b which is the univalent image of some subregion of the unit disk
![]() ${\mathbb D}$
. The supremum of all such constants b is called the Bloch constant (see [Reference Chen, Gauthier and Hengartner6, Reference Graham and Kohr13]).
${\mathbb D}$
. The supremum of all such constants b is called the Bloch constant (see [Reference Chen, Gauthier and Hengartner6, Reference Graham and Kohr13]).
In 2000, under a suitable restriction, Chen et al. [Reference Chen, Gauthier and Hengartner6] first established two non-sharp versions of Landau-type theorems for bounded harmonic mapping on the unit disk which we now recall with the help of our notation.
Theorem A [Reference Chen, Gauthier and Hengartner6, Theorem 3]
If
![]() $f\in \mathcal {BH}_M^0$
with the normalization
$f\in \mathcal {BH}_M^0$
with the normalization
![]() $f_{\overline {z}}(0)=0$
and
$f_{\overline {z}}(0)=0$
and
![]() $f_z(0)=1$
, then
$f_z(0)=1$
, then
![]() $f\in {\mathcal S}(r_1;r_1/2)$
, where
$f\in {\mathcal S}(r_1;r_1/2)$
, where
where
![]() $m\approx 6.85$
is the minimum of the function
$m\approx 6.85$
is the minimum of the function
![]() $(3-r^2)/(r(1-r^2))$
for
$(3-r^2)/(r(1-r^2))$
for
![]() $0<r<1$
.
$0<r<1$
.
Theorem B [Reference Chen, Gauthier and Hengartner6, Theorem 4]
If
![]() $f\in \mathcal {H}_0$
such that
$f\in \mathcal {H}_0$
such that
![]() $\lambda _f(0)=1$
, and
$\lambda _f(0)=1$
, and
![]() $\Lambda _f(z)\leq \Lambda $
for
$\Lambda _f(z)\leq \Lambda $
for
![]() $z\in {\mathbb D}$
, then
$z\in {\mathbb D}$
, then
![]() $f\in {\mathcal S}(r_2;r_2/2)$
, where
$f\in {\mathcal S}(r_2;r_2/2)$
, where
![]() $r_2=\frac {\pi }{4(1+\Lambda )}.$
$r_2=\frac {\pi }{4(1+\Lambda )}.$
Theorems A and B are not sharp. Better estimates were given in [Reference Dorff and Nowak12] and this topic was later dealt by a number of authors (cf. [Reference Chen and Gauthier5, Reference Chen, Ponnusamy and Rasila7, Reference Chen, Ponnusamy and Wang9, Reference Chen, Ponnusamy and Wang10, Reference Grigoryan14, Reference Huang15, Reference Liu18, Reference Liu and Chen19]). In 2008, Abdulhadi and Muhanna established two versions of Landau-type theorems for certain bounded biharmonic mappings in [Reference Abdulhadi and Muhanna2]. For later developments on this topic, we refer to [Reference Chen, Ponnusamy and Wang8, Reference Chen, Ponnusamy and Wang9, Reference Liu17, Reference Liu, Liu and Zhu20, Reference Liu, Xie and Yang22, Reference Zhu and Liu26]. In particular, sharp versions of Theorem B have been established in [Reference Huang15, Reference Liu18, Reference Liu and Chen19], and the corresponding sharp versions of Landau-type theorems for normalized bounded biharmonic mappings have also been established in [Reference Liu and Luo21].
Theorem C [Reference Liu and Luo21, Theorem 3.1]
Suppose that
![]() $\Lambda _1\geq 0$
and
$\Lambda _1\geq 0$
and
![]() $\Lambda _2>1$
. Let
$\Lambda _2>1$
. Let
![]() $F\in \mathrm {Bi}\mathcal {H}$
and
$F\in \mathrm {Bi}\mathcal {H}$
and
![]() $F(z)=|z|^2G(z)+H(z)$
, where
$F(z)=|z|^2G(z)+H(z)$
, where
![]() $G,H\in \mathcal {H}_0$
,
$G,H\in \mathcal {H}_0$
,
![]() $\lambda _{F}(0)=1,~\Lambda _{G}(z)\leq \Lambda _1$
and
$\lambda _{F}(0)=1,~\Lambda _{G}(z)\leq \Lambda _1$
and
![]() $\Lambda _{H}(z)<\Lambda _2$
for all
$\Lambda _{H}(z)<\Lambda _2$
for all
![]() $z\in {\mathbb D}$
. Then
$z\in {\mathbb D}$
. Then
![]() $F\in {\mathcal S}(r_3;R_3)$
, where
$F\in {\mathcal S}(r_3;R_3)$
, where
![]() $r_3$
is the unique root in
$r_3$
is the unique root in
![]() $(0,\,1)$
of the equation
$(0,\,1)$
of the equation
and
This result is sharp.
Theorem D [Reference Liu and Luo21, Theorem 3.3]
Suppose that
![]() $\Lambda \geq 0$
. Let
$\Lambda \geq 0$
. Let
![]() $F\in \mathrm {Bi}\mathcal {H}$
and
$F\in \mathrm {Bi}\mathcal {H}$
and
![]() $F(z)=|z|^2G(z)+H(z)$
, where
$F(z)=|z|^2G(z)+H(z)$
, where
![]() $G,H\in \mathcal {H}_0$
,
$G,H\in \mathcal {H}_0$
,
![]() $\lambda _{F}(0)=1, \Lambda _{G}(z)\leq \Lambda $
and
$\lambda _{F}(0)=1, \Lambda _{G}(z)\leq \Lambda $
and
![]() $\Lambda _H(z)\leq 1$
for all
$\Lambda _H(z)\leq 1$
for all
![]() $z\in {\mathbb D}$
. Then
$z\in {\mathbb D}$
. Then
![]() $F\in {\mathcal S}(r_4;R_4)$
, where
$F\in {\mathcal S}(r_4;R_4)$
, where
 $$ \begin{align*}r_4= \left \{ \begin{array}{rl} 1, &\mbox{ when } \displaystyle 0\leq\Lambda\leq\frac{1}{3}, \\ \displaystyle \frac{1}{\sqrt{3\Lambda}}, &\mbox{ when } \displaystyle \Lambda>\frac{1}{3}, \end{array} \right. \end{align*} $$
$$ \begin{align*}r_4= \left \{ \begin{array}{rl} 1, &\mbox{ when } \displaystyle 0\leq\Lambda\leq\frac{1}{3}, \\ \displaystyle \frac{1}{\sqrt{3\Lambda}}, &\mbox{ when } \displaystyle \Lambda>\frac{1}{3}, \end{array} \right. \end{align*} $$
and
![]() $R_4=r_4-\Lambda r_4^{3}$
. This result is sharp.
$R_4=r_4-\Lambda r_4^{3}$
. This result is sharp.
However, the sharp version of Landau-type theorem for normalized bounded harmonic mappings or Theorem A for the case of the bound
![]() $M>1$
has not been established. In 2022, Abdulhadi and Hajj established the following non-sharp Landau-type theorem for certain bounded bi-analytic functions.
$M>1$
has not been established. In 2022, Abdulhadi and Hajj established the following non-sharp Landau-type theorem for certain bounded bi-analytic functions.
Theorem E [Reference Abdulhadi and Hajj1]
Let
![]() $F\in \mathrm {Bi}\mathcal {A}_0$
and
$F\in \mathrm {Bi}\mathcal {A}_0$
and
![]() $F(z)=\bar {z}G(z)+H(z)$
, where
$F(z)=\bar {z}G(z)+H(z)$
, where
![]() $G, H\in \mathcal {A}\cap \mathcal {B}_M $
for some
$G, H\in \mathcal {A}\cap \mathcal {B}_M $
for some
![]() $M>0$
. Then,
$M>0$
. Then,
![]() $F\in {\mathcal S}(r_5;R_5)$
, where
$F\in {\mathcal S}(r_5;R_5)$
, where
 $$ \begin{align*} r_5=1-\sqrt{\frac{2M}{2M+1}} ~\mbox{ and }~ R_5=r_5-r_5^2-M\frac{r_5^2+r_5^3}{1-r_5}. \end{align*} $$
$$ \begin{align*} r_5=1-\sqrt{\frac{2M}{2M+1}} ~\mbox{ and }~ R_5=r_5-r_5^2-M\frac{r_5^2+r_5^3}{1-r_5}. \end{align*} $$
Theorem E is not sharp too.
1.3 Two natural question on Landau-type theorem
From the discussion above, a couple of natural questions arise.
Problem 1.3 Can we establish some sharp versions of Landau-type theorems for certain bounded bi-analytic functions?
Problem 1.4 Whether we can further generalize and/or improve Theorem E?
The article is organized as follows: In Section 2, we present statements of four theorems out of which one of them improves Theorem E. In addition, we provide several sharp versions of Landau-type theorems for certain bounded bi-analytic functions, which provide an affirmative answer to Problems 1.3 and 1.4. In particular, as consequence, we also obtain four sharp versions of Landau-type theorems for certain bounded biharmonic mappings. In Section 3, we state a couple of lemmas which are needed for the proofs of main results in Section 4.
2 Statement of main results and remarks
We first establish the following sharp version of Landau-type theorem for certain subclass of bounded bi-analytic functions.
Theorem 2.1 Suppose that
![]() $\Lambda _1\geq 0$
and
$\Lambda _1\geq 0$
and
![]() $\Lambda _2>1$
. Let
$\Lambda _2>1$
. Let
![]() $F\in \mathrm {Bi}\mathcal {A}_0$
and
$F\in \mathrm {Bi}\mathcal {A}_0$
and
![]() $F(z)=\bar {z}G(z)+H(z)$
, where
$F(z)=\bar {z}G(z)+H(z)$
, where
![]() $G\in \mathcal {A}_0$
,
$G\in \mathcal {A}_0$
,
![]() $H\in \mathcal {A}$
,
$H\in \mathcal {A}$
,
![]() $|G'(z)|\leq \Lambda _1$
and
$|G'(z)|\leq \Lambda _1$
and
![]() $|H'(z)|<\Lambda _2$
for all
$|H'(z)|<\Lambda _2$
for all
![]() $z\in {\mathbb D}$
. Then
$z\in {\mathbb D}$
. Then
![]() $F\in {\mathcal S}(\rho _1;\sigma _1)$
, where
$F\in {\mathcal S}(\rho _1;\sigma _1)$
, where
 $$ \begin{align} \rho_1=\frac{2\Lambda_2}{\Lambda_2(2\Lambda_1+\Lambda_2)+\sqrt{\Lambda_2^2(2\Lambda_1+\Lambda_2)^2-8\Lambda_1\Lambda_2}}, \end{align} $$
$$ \begin{align} \rho_1=\frac{2\Lambda_2}{\Lambda_2(2\Lambda_1+\Lambda_2)+\sqrt{\Lambda_2^2(2\Lambda_1+\Lambda_2)^2-8\Lambda_1\Lambda_2}}, \end{align} $$
and
 $$ \begin{align} \sigma_1=F_1(\rho_1), \quad F_1(z) = \Lambda_2^2 z-\Lambda_1|z|^2+\left(\Lambda_2^3-\Lambda_2\right)\ln\bigg(1-\frac{z}{\Lambda_2}\bigg). \end{align} $$
$$ \begin{align} \sigma_1=F_1(\rho_1), \quad F_1(z) = \Lambda_2^2 z-\Lambda_1|z|^2+\left(\Lambda_2^3-\Lambda_2\right)\ln\bigg(1-\frac{z}{\Lambda_2}\bigg). \end{align} $$
This result is sharp, with an extremal function given by
![]() $F_1(z)$
.
$F_1(z)$
.
For the case
![]() $\Lambda _1\geq 0$
and
$\Lambda _1\geq 0$
and
![]() $\Lambda _2=1$
, we will prove the following sharp version of Landau-type theorem for certain subclass of bounded bi-analytic functions.
$\Lambda _2=1$
, we will prove the following sharp version of Landau-type theorem for certain subclass of bounded bi-analytic functions.
Theorem 2.2 Suppose that
![]() $\Lambda \geq 0$
. Let
$\Lambda \geq 0$
. Let
![]() $F\in \mathrm {Bi}\mathcal {A}_0$
and
$F\in \mathrm {Bi}\mathcal {A}_0$
and
![]() $F(z)=\bar {z}G(z)+H(z)$
, where
$F(z)=\bar {z}G(z)+H(z)$
, where
![]() $G\in \mathcal {A}_0$
,
$G\in \mathcal {A}_0$
,
![]() $H\in \mathcal {A}$
,
$H\in \mathcal {A}$
,
![]() $|G'(z)|\leq \Lambda $
, and
$|G'(z)|\leq \Lambda $
, and
![]() $|H(z)|< 1$
or
$|H(z)|< 1$
or
![]() $|H'(z)|\leq 1$
for all
$|H'(z)|\leq 1$
for all
![]() $z\in {\mathbb D}$
. Then
$z\in {\mathbb D}$
. Then
![]() $F\in {\mathcal S}(\rho _2;\sigma _2)$
, where
$F\in {\mathcal S}(\rho _2;\sigma _2)$
, where
 $$ \begin{align*}\rho_2= \left \{ \begin{array}{rl} 1, &\mbox{ when } \displaystyle 0\leq\Lambda\leq\frac{1}{2},\\ \displaystyle \frac{1}{2\Lambda}, &\mbox{ when } \displaystyle \Lambda>\frac{1}{2}, \end{array}\right. \end{align*} $$
$$ \begin{align*}\rho_2= \left \{ \begin{array}{rl} 1, &\mbox{ when } \displaystyle 0\leq\Lambda\leq\frac{1}{2},\\ \displaystyle \frac{1}{2\Lambda}, &\mbox{ when } \displaystyle \Lambda>\frac{1}{2}, \end{array}\right. \end{align*} $$
and
![]() $\sigma _2=\rho _2-\Lambda \rho _2^2$
. This result is sharp.
$\sigma _2=\rho _2-\Lambda \rho _2^2$
. This result is sharp.
Remark 2.3 Note that
![]() $G\in \mathcal {A}_0$
implies that
$G\in \mathcal {A}_0$
implies that
![]() $G(z)=z G_1(z)$
with
$G(z)=z G_1(z)$
with
![]() $G_1(z)$
being analytic in
$G_1(z)$
being analytic in
![]() ${\mathbb D}$
. Thus, the bi-analytic function
${\mathbb D}$
. Thus, the bi-analytic function
![]() $F(z)=\bar {z}G(z)+H(z)$
reduces to the form
$F(z)=\bar {z}G(z)+H(z)$
reduces to the form
![]() $F(z)=|z|^2G_1(z)+H(z)$
which is clearly a biharmonic mappings. Hence, we conclude the following corollaries from Theorems 2.1 and 2.2.
$F(z)=|z|^2G_1(z)+H(z)$
which is clearly a biharmonic mappings. Hence, we conclude the following corollaries from Theorems 2.1 and 2.2.
Corollary 2.4 Suppose that
![]() $\Lambda _1\geq 0$
and
$\Lambda _1\geq 0$
and
![]() $\Lambda _2>1$
. Let
$\Lambda _2>1$
. Let
![]() $F(z)=|z|^2G(z)+H(z)$
belong to
$F(z)=|z|^2G(z)+H(z)$
belong to
![]() $\mathrm {Bi}\mathcal {H}$
, where
$\mathrm {Bi}\mathcal {H}$
, where
![]() $G\in \mathrm {Hol}({\mathbb D})$
and
$G\in \mathrm {Hol}({\mathbb D})$
and
![]() $H\in \mathcal {A}$
.
$H\in \mathcal {A}$
.
-
(1) If
 $|G(z)+zG'(z)|\leq \Lambda _1$
, and
$|G(z)+zG'(z)|\leq \Lambda _1$
, and
 $|H'(z)|<\Lambda _2$
for all
$|H'(z)|<\Lambda _2$
for all
 $z\in {\mathbb D}$
, then
$z\in {\mathbb D}$
, then
 $F\in {\mathcal S}(\rho _1;\sigma _1)$
where
$F\in {\mathcal S}(\rho _1;\sigma _1)$
where
 $\rho _1$
and
$\rho _1$
and
 $\sigma _1$
are given by (2.1) and (2.2), respectively. This result is sharp, with an extremal function
$\sigma _1$
are given by (2.1) and (2.2), respectively. This result is sharp, with an extremal function
 $F_1(z)$
given by (2.2).
$F_1(z)$
given by (2.2). -
(2) If
 $|G(z)+zG'(z)|\leq \Lambda _1$
, and
$|G(z)+zG'(z)|\leq \Lambda _1$
, and
 $|H(z)|< 1$
or
$|H(z)|< 1$
or
 $|H'(z)|\leq 1$
for all
$|H'(z)|\leq 1$
for all
 $z\in {\mathbb D}$
, then
$z\in {\mathbb D}$
, then
 $F\in {\mathcal S}(\rho _2;\sigma _2)$
where
$F\in {\mathcal S}(\rho _2;\sigma _2)$
where
 $\rho _2$
and
$\rho _2$
and
 $\sigma _2$
are as in Theorem 2.2. This result is sharp, with an extremal function given by
$\sigma _2$
are as in Theorem 2.2. This result is sharp, with an extremal function given by
 $F_2(z)=\Lambda _1 |z|^2+z$
.
$F_2(z)=\Lambda _1 |z|^2+z$
.
If we replace the condition “
![]() $|G(z)+zG'(z)|\leq \Lambda _1$
for all
$|G(z)+zG'(z)|\leq \Lambda _1$
for all
![]() $z\in {\mathbb D}$
” by the conditions “
$z\in {\mathbb D}$
” by the conditions “
![]() $G(0)=0$
and
$G(0)=0$
and
![]() $|G'(z)|\leq \Lambda _1$
for all
$|G'(z)|\leq \Lambda _1$
for all
![]() $z\in {\mathbb D}$
” in Corollary 2.4, then, by Theorems C and D, we have the following sharp versions of Landau-type theorems for the special subclasses of bounded biharmonic mappings.
$z\in {\mathbb D}$
” in Corollary 2.4, then, by Theorems C and D, we have the following sharp versions of Landau-type theorems for the special subclasses of bounded biharmonic mappings.
Corollary 2.5 Suppose that
![]() $\Lambda _1\geq 0$
and
$\Lambda _1\geq 0$
and
![]() $\Lambda _2>1$
. Let
$\Lambda _2>1$
. Let
![]() $F(z)=|z|^2G(z)+H(z)$
belong to
$F(z)=|z|^2G(z)+H(z)$
belong to
![]() $\mathrm {Bi}\mathcal {H}$
, where
$\mathrm {Bi}\mathcal {H}$
, where
![]() $G\in \mathrm {Hol}({\mathbb D})$
and
$G\in \mathrm {Hol}({\mathbb D})$
and
![]() $H\in \mathcal {A}$
.
$H\in \mathcal {A}$
.
-
(1) If
 $|G'(z)|\leq \Lambda _1$
, and
$|G'(z)|\leq \Lambda _1$
, and
 $|H'(z)|<\Lambda _2$
for all
$|H'(z)|<\Lambda _2$
for all
 $z\in {\mathbb D}$
, then
$z\in {\mathbb D}$
, then
 $F\in {\mathcal S}(r_3;R_3)$
, where
$F\in {\mathcal S}(r_3;R_3)$
, where
 $r_3$
and
$r_3$
and
 $R_3$
are as in Theorem C. This result is sharp, with an extremal function given by
$R_3$
are as in Theorem C. This result is sharp, with an extremal function given by  $$ \begin{align*} F_0(z) =\Lambda_2^2 z-\Lambda_1|z|^2z+\left(\Lambda_2^3-\Lambda_2\right)\ln\bigg(1-\frac{z}{\Lambda_2}\bigg). \end{align*} $$
$$ \begin{align*} F_0(z) =\Lambda_2^2 z-\Lambda_1|z|^2z+\left(\Lambda_2^3-\Lambda_2\right)\ln\bigg(1-\frac{z}{\Lambda_2}\bigg). \end{align*} $$
-
(2) If
 $|G'(z)|\leq \Lambda _1$
, and
$|G'(z)|\leq \Lambda _1$
, and
 $|H(z)|< 1$
or
$|H(z)|< 1$
or
 $|H'(z)|\leq 1$
for all
$|H'(z)|\leq 1$
for all
 $z\in {\mathbb D}$
, then
$z\in {\mathbb D}$
, then
 $F\in {\mathcal S}(r_4;R_4)$
, where
$F\in {\mathcal S}(r_4;R_4)$
, where
 $r_4$
and
$r_4$
and
 $R_4$
are as in Theorem D. This result is sharp, with an extremal function given by
$R_4$
are as in Theorem D. This result is sharp, with an extremal function given by
 $F_2(z)=\Lambda _1 |z|^2+z$
.
$F_2(z)=\Lambda _1 |z|^2+z$
.
Now, we improve Theorem E by establishing the following results.
Theorem 2.6 Let
![]() $F\in \mathrm {Bi}\mathcal {A}_0$
and
$F\in \mathrm {Bi}\mathcal {A}_0$
and
![]() $F(z)=\bar {z}G(z)+H(z)$
, where
$F(z)=\bar {z}G(z)+H(z)$
, where
![]() $G\in \mathcal {B}_{M_1}\cap \mathcal {A}$
and
$G\in \mathcal {B}_{M_1}\cap \mathcal {A}$
and
![]() $H\in \mathcal {B}_{M_2}\cap \mathcal {A}$
for some
$H\in \mathcal {B}_{M_2}\cap \mathcal {A}$
for some
![]() $M_1>0$
and
$M_1>0$
and
![]() $M_2>0$
. Then
$M_2>0$
. Then
![]() $F\in {\mathcal S}(\rho _3;\sigma _3)$
, where
$F\in {\mathcal S}(\rho _3;\sigma _3)$
, where
![]() $\rho _3$
is the unique root in
$\rho _3$
is the unique root in
![]() $(0,1)$
of the equation
$(0,1)$
of the equation
 $$ \begin{align} 1-\Big(M_2-\frac{1}{M_2}\Big)\frac{2r-r^2}{(1-r)^2}-\Big(M_1-\frac{1}{M_1}\Big)\frac{(3-2r)r^2}{(1-r)^2}-2r=0, \end{align} $$
$$ \begin{align} 1-\Big(M_2-\frac{1}{M_2}\Big)\frac{2r-r^2}{(1-r)^2}-\Big(M_1-\frac{1}{M_1}\Big)\frac{(3-2r)r^2}{(1-r)^2}-2r=0, \end{align} $$
and
 $$ \begin{align*} \sigma_3=\rho_3-\rho_3^2-\Big(M_2-\frac{1}{M_2}\Big)\frac{\rho_3^2}{1-\rho_3}-\Big(M_1-\frac{1}{M_1}\Big)\frac{\rho_3^3}{1-\rho_3}. \end{align*} $$
$$ \begin{align*} \sigma_3=\rho_3-\rho_3^2-\Big(M_2-\frac{1}{M_2}\Big)\frac{\rho_3^2}{1-\rho_3}-\Big(M_1-\frac{1}{M_1}\Big)\frac{\rho_3^3}{1-\rho_3}. \end{align*} $$
Remark 2.7 If we set
![]() $M_1=M_2=1$
in Theorem 2.6, then it is clear that
$M_1=M_2=1$
in Theorem 2.6, then it is clear that
![]() $G(z)=z$
and
$G(z)=z$
and
![]() $H(z)=z$
by Schwarz lemma. Thus,
$H(z)=z$
by Schwarz lemma. Thus,
![]() $\rho _3=\frac {1}{2}$
and
$\rho _3=\frac {1}{2}$
and
![]() $\sigma _3=\frac {1}{4}$
are sharp, with an extremal function
$\sigma _3=\frac {1}{4}$
are sharp, with an extremal function
![]() $F_3(z)=|z|^2+z$
. Moreover, if we set
$F_3(z)=|z|^2+z$
. Moreover, if we set
![]() $M_1=M_2=M$
in Theorem 2.6, then one can easily gets an improved version of Theorem E.
$M_1=M_2=M$
in Theorem 2.6, then one can easily gets an improved version of Theorem E.
Furthermore, as with Remark 2.3, we easily have the following.
Corollary 2.8 Let
![]() $F(z)=|z|^2G(z)+H(z)$
belong to
$F(z)=|z|^2G(z)+H(z)$
belong to
![]() $\mathrm {Bi}\mathcal {H}$
, where
$\mathrm {Bi}\mathcal {H}$
, where
![]() $G\in \mathcal {B}_{M_1}\cap \mathcal {A}$
and
$G\in \mathcal {B}_{M_1}\cap \mathcal {A}$
and
![]() $H\in \mathcal {B}_{M_2}\cap \mathcal {A}$
for some
$H\in \mathcal {B}_{M_2}\cap \mathcal {A}$
for some
![]() $M_1>0$
and
$M_1>0$
and
![]() $M_2>0$
. Then
$M_2>0$
. Then
![]() $F\in {\mathcal S}(\rho _3;\sigma _3)$
, where
$F\in {\mathcal S}(\rho _3;\sigma _3)$
, where
![]() $\rho _3$
and
$\rho _3$
and
![]() $\sigma _3$
are as in Theorem 2.6.
$\sigma _3$
are as in Theorem 2.6.
Remark 2.9 Again, if
![]() $M_1=M_2=1$
, then we have
$M_1=M_2=1$
, then we have
![]() $\rho _3=\frac {1}{2}$
and
$\rho _3=\frac {1}{2}$
and
![]() $\sigma _3=\frac {1}{4}$
with an extremal function
$\sigma _3=\frac {1}{4}$
with an extremal function
![]() $F_3(z)=|z|^2+z$
.
$F_3(z)=|z|^2+z$
.
Finally, we improve Theorem 2.6 by establishing the following theorem.
Theorem 2.10 Let
![]() $F\in \mathrm {Bi}\mathcal {A}_0$
and
$F\in \mathrm {Bi}\mathcal {A}_0$
and
![]() $F(z)=\bar {z}G(z)+H(z)$
, where
$F(z)=\bar {z}G(z)+H(z)$
, where
![]() $0\not \equiv G \in \mathcal {B}_{M_1}\cap \mathcal {A}$
and
$0\not \equiv G \in \mathcal {B}_{M_1}\cap \mathcal {A}$
and
![]() $H\in \mathcal {B}_{M_2}\cap \mathcal {A}$
for some
$H\in \mathcal {B}_{M_2}\cap \mathcal {A}$
for some
![]() $M_1>0$
and
$M_1>0$
and
![]() $M_2>0$
. Then F is sense-preserving, univalent and fully starlike in the disk
$M_2>0$
. Then F is sense-preserving, univalent and fully starlike in the disk
![]() ${\mathbb D}_{\rho _3}$
, where
${\mathbb D}_{\rho _3}$
, where
![]() $\rho _3$
is the unique root in
$\rho _3$
is the unique root in
![]() $(0,\,1)$
of equation (2.3).
$(0,\,1)$
of equation (2.3).
3 Key lemmas
In order to prove our main results, we need the following lemmas which play a key role in establishing the subsequent results in Section 4.
Lemma 3.1 Let
![]() $H\in \mathcal {A}_{1}$
and
$H\in \mathcal {A}_{1}$
and
![]() $|H'(z)|<\Lambda $
for all
$|H'(z)|<\Lambda $
for all
![]() $z\in {\mathbb D}$
and for some
$z\in {\mathbb D}$
and for some
![]() $\Lambda>1$
.
$\Lambda>1$
.
-
(1) For all
 $z_1,z_2\in {\mathbb D}_r\, (0<r<1, z_1\neq z_2)$
, we have where
$z_1,z_2\in {\mathbb D}_r\, (0<r<1, z_1\neq z_2)$
, we have where $$ \begin{align*} |H(z_1)-H(z_2)|=\bigg|\int_{\gamma }H'(z)\,dz\bigg|\geq\Lambda\, \frac{1-\Lambda r}{\Lambda-r}\, |z_1-z_2|, \end{align*} $$
$$ \begin{align*} |H(z_1)-H(z_2)|=\bigg|\int_{\gamma }H'(z)\,dz\bigg|\geq\Lambda\, \frac{1-\Lambda r}{\Lambda-r}\, |z_1-z_2|, \end{align*} $$
 $\gamma =[z_1,z_2]$
denotes the closed line segment joining
$\gamma =[z_1,z_2]$
denotes the closed line segment joining
 $z_1$
and
$z_1$
and
 $z_2$
.
$z_2$
.
-
(2) For
 $z'\in \partial {\mathbb D}_r\, (0<r<1)$
with
$z'\in \partial {\mathbb D}_r\, (0<r<1)$
with
 $w'=H(z')\in H(\partial {\mathbb D}_r)$
and
$w'=H(z')\in H(\partial {\mathbb D}_r)$
and
 $|w'|=\min \{|w|:\,w\in H (\partial {\mathbb D}_r)\}$
, set
$|w'|=\min \{|w|:\,w\in H (\partial {\mathbb D}_r)\}$
, set
 $\gamma _0=H^{-1}(\Gamma _0)$
and
$\gamma _0=H^{-1}(\Gamma _0)$
and
 $\Gamma _0= [0,w'] $
denotes the closed line segment joining the origin and
$\Gamma _0= [0,w'] $
denotes the closed line segment joining the origin and
 $w'$
. Then we have
$w'$
. Then we have  $$ \begin{align*} |H(z')| \geq\Lambda\int_{0}^{r}\frac{\frac{1}{\Lambda}-t}{1-\frac{t}{\Lambda}}\,dt=\Lambda^2 r+(\Lambda^3-\Lambda)\ln\left(1-\frac{r}{\Lambda}\right). \end{align*} $$
$$ \begin{align*} |H(z')| \geq\Lambda\int_{0}^{r}\frac{\frac{1}{\Lambda}-t}{1-\frac{t}{\Lambda}}\,dt=\Lambda^2 r+(\Lambda^3-\Lambda)\ln\left(1-\frac{r}{\Lambda}\right). \end{align*} $$
Proof Set
![]() $\omega (z)=H'(z)/\Lambda $
,
$\omega (z)=H'(z)/\Lambda $
,
![]() $z\in {\mathbb D}$
. Then
$z\in {\mathbb D}$
. Then
![]() $\omega \in \mathcal {B}_1$
with
$\omega \in \mathcal {B}_1$
with
![]() $\alpha :=\omega (0)=\frac {H'(0)}{\Lambda }=\frac {1}{\Lambda }.$
Using Schwarz–Pick Lemma, we have
$\alpha :=\omega (0)=\frac {H'(0)}{\Lambda }=\frac {1}{\Lambda }.$
Using Schwarz–Pick Lemma, we have
 $$ \begin{align*} \frac{\frac{1}{\Lambda}-r}{1-\frac{r}{\Lambda}}= \frac{\alpha -r}{1-\alpha r} \leq \mathrm{Re}\, \omega(z) \leq |\omega(z)|\leq \frac{\alpha +r }{1+\alpha r} , \quad z\in {\mathbb D}_r. \end{align*} $$
$$ \begin{align*} \frac{\frac{1}{\Lambda}-r}{1-\frac{r}{\Lambda}}= \frac{\alpha -r}{1-\alpha r} \leq \mathrm{Re}\, \omega(z) \leq |\omega(z)|\leq \frac{\alpha +r }{1+\alpha r} , \quad z\in {\mathbb D}_r. \end{align*} $$
(1) Fix
![]() $z_1,z_2\in {\mathbb D}_r\, (0<r<1)$
with
$z_1,z_2\in {\mathbb D}_r\, (0<r<1)$
with
![]() $z_1\neq z_2$
, set
$z_1\neq z_2$
, set
![]() $\theta _0=\arg (z_2-z_1)$
. Then
$\theta _0=\arg (z_2-z_1)$
. Then
 $$ \begin{align*} \hspace{1cm}|H(z_1)-H(z_2)|&= \bigg|\int_{\overline{\gamma }}H'(z)\,dz\bigg|=\left| \int_{\gamma}\Lambda\, \omega(z)e^{i\theta_0}\,|dz|\right|\\ &\geq \Lambda\int_{\gamma}\mathrm{Re}\, \omega(z)|dz|\\ &\geq \Lambda\, \int_{\gamma}\frac{\frac{1}{\Lambda}-r}{1-\frac{r}{\Lambda}}\,|dz|=\Lambda\, \frac{1-\Lambda r}{\Lambda-r}\, |z_1-z_2|. \end{align*} $$
$$ \begin{align*} \hspace{1cm}|H(z_1)-H(z_2)|&= \bigg|\int_{\overline{\gamma }}H'(z)\,dz\bigg|=\left| \int_{\gamma}\Lambda\, \omega(z)e^{i\theta_0}\,|dz|\right|\\ &\geq \Lambda\int_{\gamma}\mathrm{Re}\, \omega(z)|dz|\\ &\geq \Lambda\, \int_{\gamma}\frac{\frac{1}{\Lambda}-r}{1-\frac{r}{\Lambda}}\,|dz|=\Lambda\, \frac{1-\Lambda r}{\Lambda-r}\, |z_1-z_2|. \end{align*} $$
(2) For
![]() $z'\in \partial {\mathbb D}_r\, (0<r<1)$
with
$z'\in \partial {\mathbb D}_r\, (0<r<1)$
with
![]() $w'=H(z')\in H(\partial {\mathbb D}_r)$
,
$w'=H(z')\in H(\partial {\mathbb D}_r)$
,
![]() $|w'|=\min \{|w|:\,w\in F (\partial {\mathbb D}_r ) \}$
and
$|w'|=\min \{|w|:\,w\in F (\partial {\mathbb D}_r ) \}$
and
![]() $\Gamma _0=[0,w]$
, set
$\Gamma _0=[0,w]$
, set
![]() $\gamma _0=H^{-1}(\Gamma _0)$
so that
$\gamma _0=H^{-1}(\Gamma _0)$
so that
 $$ \begin{align*} \hspace{1.5cm}|H(z')|&=|w'|= \int_{\gamma_0}|H'(\zeta)|\,|d\zeta|=\Lambda\int_{\gamma_0}|\omega (\zeta)|\,|d\zeta|\\ &\geq \Lambda\int_{0}^{r} \frac{\frac{1}{\Lambda}-t}{1-\frac{t}{\Lambda}}dt=\Lambda^2 r+(\Lambda^3-\Lambda)\ln\left(1-\frac{r}{\Lambda}\right), \end{align*} $$
$$ \begin{align*} \hspace{1.5cm}|H(z')|&=|w'|= \int_{\gamma_0}|H'(\zeta)|\,|d\zeta|=\Lambda\int_{\gamma_0}|\omega (\zeta)|\,|d\zeta|\\ &\geq \Lambda\int_{0}^{r} \frac{\frac{1}{\Lambda}-t}{1-\frac{t}{\Lambda}}dt=\Lambda^2 r+(\Lambda^3-\Lambda)\ln\left(1-\frac{r}{\Lambda}\right), \end{align*} $$
and the proof is complete.
Lemma 3.2 (Carlson lemma, [Reference Carlson4])
If
![]() $F\in \mathcal {B}_{1}$
and
$F\in \mathcal {B}_{1}$
and
![]() $F(z)=\sum _{n=0}^{\infty }a_nz^{n}$
, then the following inequalities hold:
$F(z)=\sum _{n=0}^{\infty }a_nz^{n}$
, then the following inequalities hold:
-
(a)
 $|a_{2n+1}|\leq 1-|a_0|^2-\cdots - |a_n|^2,\, n=0, 1, \ldots $
.
$|a_{2n+1}|\leq 1-|a_0|^2-\cdots - |a_n|^2,\, n=0, 1, \ldots $
. -
(b)
 $|a_{2n}|\leq 1-|a_0|^2-\cdots - |a_{n-1}|^2-\frac {|a_n|^2}{1+|a_0|},\, n=1, 2, \ldots $
.
$|a_{2n}|\leq 1-|a_0|^2-\cdots - |a_{n-1}|^2-\frac {|a_n|^2}{1+|a_0|},\, n=1, 2, \ldots $
.
These inequalities are sharp.
Lemma 3.3 If
![]() $f\in \mathcal {B}_M\cap \mathcal {A}_0$
for some
$f\in \mathcal {B}_M\cap \mathcal {A}_0$
for some
![]() $M>0$
and
$M>0$
and
![]() $f(z)=\sum _{n=1}^{\infty }a_nz^n$
, then
$f(z)=\sum _{n=1}^{\infty }a_nz^n$
, then
-
(a)
 $\displaystyle |a_{2n}|\leq M\left [1- \left (\frac {|a_1|^2+ \cdots + |a_n|^2}{M^2}\right )\right ],\, n=1, 2, \ldots $
.
$\displaystyle |a_{2n}|\leq M\left [1- \left (\frac {|a_1|^2+ \cdots + |a_n|^2}{M^2}\right )\right ],\, n=1, 2, \ldots $
. -
(b)
 $\displaystyle |a_{2n+1 }|\leq M\left [1 - \left (\frac {|a_1|^2 + \cdots + |a_n|^2}{M^2}\right ) - \frac {|a_{n+1}|^2}{M(M+|a_1|)} \right ], \, n=1, 2, \ldots $
.
$\displaystyle |a_{2n+1 }|\leq M\left [1 - \left (\frac {|a_1|^2 + \cdots + |a_n|^2}{M^2}\right ) - \frac {|a_{n+1}|^2}{M(M+|a_1|)} \right ], \, n=1, 2, \ldots $
.
In particular, if
![]() $|a_1|=1$
, i.e., if
$|a_1|=1$
, i.e., if
![]() $f\in \mathcal {B}_M\cap \mathcal {A}$
, then
$f\in \mathcal {B}_M\cap \mathcal {A}$
, then
![]() $M\geq 1$
and
$M\geq 1$
and
These inequalities are sharp, with the extremal functions
![]() $f_n(z)$
, where
$f_n(z)$
, where
 $$ \begin{align*} f_1(z)=z,\quad f_n(z)=Mz \frac{1-M z^{n-1}}{M-z^{n-1}}=z -\Big(M-\frac{1}{M}\Big)z^n -\sum\limits_{k=3}^\infty \frac{M^2-1}{M^{k-1}}z^{(n-1)(k-1)+1} \end{align*} $$
$$ \begin{align*} f_1(z)=z,\quad f_n(z)=Mz \frac{1-M z^{n-1}}{M-z^{n-1}}=z -\Big(M-\frac{1}{M}\Big)z^n -\sum\limits_{k=3}^\infty \frac{M^2-1}{M^{k-1}}z^{(n-1)(k-1)+1} \end{align*} $$
for
![]() $n=2,3,\ldots $
.
$n=2,3,\ldots $
.
Proof Setting
![]() $g(z)=\frac {f(z)}{M z}$
for
$g(z)=\frac {f(z)}{M z}$
for
![]() $z\in {\mathbb D}\backslash \{0\}$
, and
$z\in {\mathbb D}\backslash \{0\}$
, and
![]() $g(0)=\frac {a_1}{M}$
, shows that
$g(0)=\frac {a_1}{M}$
, shows that
![]() $g\in \mathcal {B}_1$
and
$g\in \mathcal {B}_1$
and
 $$ \begin{align*} g(z)= \sum_{n=0}^{\infty}b_nz^{n}, \end{align*} $$
$$ \begin{align*} g(z)= \sum_{n=0}^{\infty}b_nz^{n}, \end{align*} $$
where
![]() $b_n= a_{n+1}/M$
for
$b_n= a_{n+1}/M$
for
![]() $n\geq 0$
. Note that
$n\geq 0$
. Note that
![]() $b_0=a_1/M$
. Applying Lemma 3.2 to the coefficients
$b_0=a_1/M$
. Applying Lemma 3.2 to the coefficients
![]() $b_n$
of g gives the desired inequality.
$b_n$
of g gives the desired inequality.
In particular, if
![]() $|a_1|=1$
, then we have
$|a_1|=1$
, then we have
![]() $M\geq 1$
and it follows from (a) and (b) that
$M\geq 1$
and it follows from (a) and (b) that
 $$ \begin{align*} |a_{n}|\leq M\left (1- \frac{|a_1|^2}{M^2}\right ) =M-\frac{1}{M} ~\mbox{ for } n\geq 2,~ \end{align*} $$
$$ \begin{align*} |a_{n}|\leq M\left (1- \frac{|a_1|^2}{M^2}\right ) =M-\frac{1}{M} ~\mbox{ for } n\geq 2,~ \end{align*} $$
and it is evident that equalities hold for all
![]() $n=2,3,\ldots $
for the functions
$n=2,3,\ldots $
for the functions
 $$ \begin{align*} f_n(z)=Mz\frac{1-M z^{n-1}}{M-z^{n-1}}=z-\Big(M-\frac{1}{M}\Big)z^n-\sum\limits_{k=3}^\infty\frac{M^2-1}{M^{k-1}}z^{(n-1)(k-1)+1}, \end{align*} $$
$$ \begin{align*} f_n(z)=Mz\frac{1-M z^{n-1}}{M-z^{n-1}}=z-\Big(M-\frac{1}{M}\Big)z^n-\sum\limits_{k=3}^\infty\frac{M^2-1}{M^{k-1}}z^{(n-1)(k-1)+1}, \end{align*} $$
and the proof is complete.
Lemma 3.4
Let
![]() $F(z)=\bar {z}G(z)+H(z)$
be a bi-analytic function of the unit disk
$F(z)=\bar {z}G(z)+H(z)$
be a bi-analytic function of the unit disk
![]() ${\mathbb D}$
, where
${\mathbb D}$
, where
![]() $G(z)=\sum \limits _{n=1}^\infty a_n z^n\not \equiv 0$
and
$G(z)=\sum \limits _{n=1}^\infty a_n z^n\not \equiv 0$
and
![]() $H(z)=z+\sum \limits _{n=2}^\infty b_n z^n$
are analytic in
$H(z)=z+\sum \limits _{n=2}^\infty b_n z^n$
are analytic in
![]() ${\mathbb D}$
, and satisfy the condition
${\mathbb D}$
, and satisfy the condition
 $$ \begin{align} \sum\limits_{n=2}^\infty n|b_n|r^{n-1}+\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\leq 1, \end{align} $$
$$ \begin{align} \sum\limits_{n=2}^\infty n|b_n|r^{n-1}+\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\leq 1, \end{align} $$
for some
![]() $r\in (0, 1)$
. Then
$r\in (0, 1)$
. Then
![]() $F(z)$
is sense-preserving, univalent and fully starlike in the disk
$F(z)$
is sense-preserving, univalent and fully starlike in the disk
![]() ${\mathbb D}_r$
.
${\mathbb D}_r$
.
Proof We may use arguments similar to those in the proof of [Reference Luo and Ponnusamy23, Lemma 1]. For the sake of readability, we provide the details. Elementary computation gives
 $$ \begin{align} z F_z(z)-\bar{z}F_{\bar{z}}(z)-F(z) =\bar{z}\sum\limits_{n=1}^\infty (n-2)a_n z^n+\sum\limits_{n=2}^\infty (n-1)b_n z^n. \end{align} $$
$$ \begin{align} z F_z(z)-\bar{z}F_{\bar{z}}(z)-F(z) =\bar{z}\sum\limits_{n=1}^\infty (n-2)a_n z^n+\sum\limits_{n=2}^\infty (n-1)b_n z^n. \end{align} $$
Evidently,
![]() $J_{F}(0)=1$
. Now, we fix
$J_{F}(0)=1$
. Now, we fix
![]() $r\in (0, 1]$
and find that
$r\in (0, 1]$
and find that
 $$ \begin{align*} |F_z(z)|-|F_{\bar{z}}(z)|&= \Big|\bar{z}\sum\limits_{n=1}^\infty n a_n z^{n-1}+1+\sum\limits_{n=2}^\infty n b_n z^{n-1}\Big| -\Big|\sum\limits_{n=1}^\infty a_n z^n\Big|\\ &> 1-\sum\limits_{n=2}^\infty n|b_n|r^{n-1}-\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\geq 0, \end{align*} $$
$$ \begin{align*} |F_z(z)|-|F_{\bar{z}}(z)|&= \Big|\bar{z}\sum\limits_{n=1}^\infty n a_n z^{n-1}+1+\sum\limits_{n=2}^\infty n b_n z^{n-1}\Big| -\Big|\sum\limits_{n=1}^\infty a_n z^n\Big|\\ &> 1-\sum\limits_{n=2}^\infty n|b_n|r^{n-1}-\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\geq 0, \end{align*} $$
and therefore,
![]() $J_{F}(z)= (|F_z(z)|+|F_{\bar {z}}(z)|)(|F_z(z)|-|F_{\bar {z}}(z)|)>0$
for
$J_{F}(z)= (|F_z(z)|+|F_{\bar {z}}(z)|)(|F_z(z)|-|F_{\bar {z}}(z)|)>0$
for
![]() $|z|<r$
.
$|z|<r$
.
Thus, F is sense-preserving in
![]() ${\mathbb D}_r$
. Finally, fix
${\mathbb D}_r$
. Finally, fix
![]() $r_0\in (0, r]$
and consider the circle
$r_0\in (0, r]$
and consider the circle
![]() $\partial {\mathbb D}_{r_0}=\{z:\,|z|=r_0\}$
. For
$\partial {\mathbb D}_{r_0}=\{z:\,|z|=r_0\}$
. For
![]() $z\in \partial {\mathbb D}_{r_0}$
, it follows from
$z\in \partial {\mathbb D}_{r_0}$
, it follows from
![]() $G(z)=\sum \limits _{n=1}^\infty a_n z^n\not \equiv 0$
, (3.1) and (3.2) that
$G(z)=\sum \limits _{n=1}^\infty a_n z^n\not \equiv 0$
, (3.1) and (3.2) that
 $$ \begin{align*} |z F_z(z)-\bar{z}F_{\bar{z}}(z)-F(z)|&\leq \sum\limits_{n=1}^\infty |n-2|\,|a_n|\,|z|^{n+1}+\sum\limits_{n=2}^\infty (n-1)|b_n|\,|z|^n\\ &=|z| \Big(\sum\limits_{n=2}^\infty n|b_n|\,|z|^{n-1}+\sum\limits_{n=1}^\infty (n+1)|a_n|\,|z|^{n}\Big)\\ &\quad -|a_1|\,|z|^2-3\sum\limits_{n=2}^\infty |a_n|\,|z|^{n+1}-\sum\limits_{n=2}^\infty |b_n|\,|z|^{n}\\ &< |z|-\sum\limits_{n=2}^\infty |b_n|\,|z|^{n}-|\bar{z}|\sum\limits_{n=1}^\infty |a_n|\,|z|^{n}\\ &\leq |H(z)|-|\bar{z}G(z)|\leq |F(z)|, \end{align*} $$
$$ \begin{align*} |z F_z(z)-\bar{z}F_{\bar{z}}(z)-F(z)|&\leq \sum\limits_{n=1}^\infty |n-2|\,|a_n|\,|z|^{n+1}+\sum\limits_{n=2}^\infty (n-1)|b_n|\,|z|^n\\ &=|z| \Big(\sum\limits_{n=2}^\infty n|b_n|\,|z|^{n-1}+\sum\limits_{n=1}^\infty (n+1)|a_n|\,|z|^{n}\Big)\\ &\quad -|a_1|\,|z|^2-3\sum\limits_{n=2}^\infty |a_n|\,|z|^{n+1}-\sum\limits_{n=2}^\infty |b_n|\,|z|^{n}\\ &< |z|-\sum\limits_{n=2}^\infty |b_n|\,|z|^{n}-|\bar{z}|\sum\limits_{n=1}^\infty |a_n|\,|z|^{n}\\ &\leq |H(z)|-|\bar{z}G(z)|\leq |F(z)|, \end{align*} $$
which implies that
 $$ \begin{align*} \bigg|\frac{z F_z(z)- \bar{z} F_{\bar z}(z)}{F(z)}-1\bigg|<1\quad\mbox{ for } |z|=r_0. \end{align*} $$
$$ \begin{align*} \bigg|\frac{z F_z(z)- \bar{z} F_{\bar z}(z)}{F(z)}-1\bigg|<1\quad\mbox{ for } |z|=r_0. \end{align*} $$
Thus, we obtain that F is univalent on
![]() $\partial {\mathbb D}_{r_0}$
, and it maps
$\partial {\mathbb D}_{r_0}$
, and it maps
![]() $\partial {\mathbb D}_{r_0}$
onto a starlike curve. Hence, by the sense-preserving property and the degree principle, we see that F is univalent in
$\partial {\mathbb D}_{r_0}$
onto a starlike curve. Hence, by the sense-preserving property and the degree principle, we see that F is univalent in
![]() ${\mathbb D}_{r_0}$
. Since
${\mathbb D}_{r_0}$
. Since
![]() $r_0\in (0, r]$
is arbitrary, we conclude that F is univalent and fully starlike in
$r_0\in (0, r]$
is arbitrary, we conclude that F is univalent and fully starlike in
![]() ${\mathbb D}_r$
. The proof is complete.
${\mathbb D}_r$
. The proof is complete.
4 Proofs of the main results
4.1 Proof of Theorem 2.1
By the assumption on
![]() $G\in \mathcal {A}_0$
, we have
$G\in \mathcal {A}_0$
, we have
 $$ \begin{align} |G(z)|=\bigg|\int_{[0,z]}G'(z)\, dz\bigg|\leq \int_{[0,z]}|G'(z)|\,|dz|\leq \Lambda_1 |z|,\ \ z\in {\mathbb D}. \end{align} $$
$$ \begin{align} |G(z)|=\bigg|\int_{[0,z]}G'(z)\, dz\bigg|\leq \int_{[0,z]}|G'(z)|\,|dz|\leq \Lambda_1 |z|,\ \ z\in {\mathbb D}. \end{align} $$
We first prove that F is univalent in the disk
![]() ${\mathbb D}_{\rho _1}$
. Choose, for all
${\mathbb D}_{\rho _1}$
. Choose, for all
![]() $z_1,z_2\in {\mathbb D}_r\, (0<r<\rho _1$
,
$z_1,z_2\in {\mathbb D}_r\, (0<r<\rho _1$
,
![]() $z_1\neq z_2)$
, where
$z_1\neq z_2)$
, where
![]() $\rho _1$
is defined by (2.1). As
$\rho _1$
is defined by (2.1). As
![]() $H'(0)=1$
,
$H'(0)=1$
,
![]() $|G'(z)|\leq \Lambda _1$
and
$|G'(z)|\leq \Lambda _1$
and
![]() $|H'(z)|<\Lambda _2$
for all
$|H'(z)|<\Lambda _2$
for all
![]() $z\in {\mathbb D}$
, we obtain from Lemma 3.1 that
$z\in {\mathbb D}$
, we obtain from Lemma 3.1 that
 $$ \begin{align*} |F(z_2)-F(z_1)|&= \left|\int_{[z_1,z_2]}F_z(z)\,dz+F_{\bar{z}}(z)\,d\bar{z}\right| \, =\left|\int_{[z_1,z_2]}\left(\bar{z}G'(z)+H'(z)\right)dz+G(z)\,d\bar{z}\right|\nonumber\\ &\geq \bigg|\int_{[z_1,z_2]}H'(z)\,dz\bigg|-\bigg|\int_{[z_1,z_2]}\bar{z}G'(z)\,dz+G(z)\,d\bar{z}\bigg|\\ &\geq |z_1-z_2|\left(\Lambda_2 \frac{1-\Lambda_2 r}{\Lambda_2-r}-2\Lambda_1r\right)\nonumber\\ &= |z_1-z_2|\cdot\frac{2\Lambda_1r^2-\Lambda_2(2\Lambda_1+\Lambda_2)r+\Lambda_2}{\Lambda_2-r}\nonumber\\ &= |z_1-z_2|\frac{2\Lambda_1(r-\rho_1)(r-A)}{\Lambda_2-r},\nonumber \end{align*} $$
$$ \begin{align*} |F(z_2)-F(z_1)|&= \left|\int_{[z_1,z_2]}F_z(z)\,dz+F_{\bar{z}}(z)\,d\bar{z}\right| \, =\left|\int_{[z_1,z_2]}\left(\bar{z}G'(z)+H'(z)\right)dz+G(z)\,d\bar{z}\right|\nonumber\\ &\geq \bigg|\int_{[z_1,z_2]}H'(z)\,dz\bigg|-\bigg|\int_{[z_1,z_2]}\bar{z}G'(z)\,dz+G(z)\,d\bar{z}\bigg|\\ &\geq |z_1-z_2|\left(\Lambda_2 \frac{1-\Lambda_2 r}{\Lambda_2-r}-2\Lambda_1r\right)\nonumber\\ &= |z_1-z_2|\cdot\frac{2\Lambda_1r^2-\Lambda_2(2\Lambda_1+\Lambda_2)r+\Lambda_2}{\Lambda_2-r}\nonumber\\ &= |z_1-z_2|\frac{2\Lambda_1(r-\rho_1)(r-A)}{\Lambda_2-r},\nonumber \end{align*} $$
which is positive, if
![]() $r<\rho _1$
, where
$r<\rho _1$
, where
 $$\begin{align*} A=\frac{\Lambda_2(2\Lambda_1+\Lambda_2)+\sqrt{\Lambda_2^2(2\Lambda_1+\Lambda_2)^2-8\Lambda_1\Lambda_2}}{4\Lambda_1}. \end{align*}$$
$$\begin{align*} A=\frac{\Lambda_2(2\Lambda_1+\Lambda_2)+\sqrt{\Lambda_2^2(2\Lambda_1+\Lambda_2)^2-8\Lambda_1\Lambda_2}}{4\Lambda_1}. \end{align*}$$
This proves the univalency of F in the disk
![]() ${\mathbb D}_{\rho _1}$
.
${\mathbb D}_{\rho _1}$
.
Next, we prove that
![]() $F({\mathbb D}_{\rho _1}) \supseteq {\mathbb D}_{\sigma _1}$
, where
$F({\mathbb D}_{\rho _1}) \supseteq {\mathbb D}_{\sigma _1}$
, where
![]() $\sigma _1$
is defined by (2.2). First, we note that
$\sigma _1$
is defined by (2.2). First, we note that
![]() $F(0)=0$
, for
$F(0)=0$
, for
![]() $z'\in \partial {\mathbb D}_{\rho _1}$
with
$z'\in \partial {\mathbb D}_{\rho _1}$
with
![]() $w'=F(z')\in F(\partial {\mathbb D}_{\rho _1})$
and
$w'=F(z')\in F(\partial {\mathbb D}_{\rho _1})$
and
![]() $|w'|=\min \{|w|:\,w\in F (\partial {\mathbb D}_{\rho _1} ) \}$
. By (4.1) and Lemma 3.1, we have that
$|w'|=\min \{|w|:\,w\in F (\partial {\mathbb D}_{\rho _1} ) \}$
. By (4.1) and Lemma 3.1, we have that
which implies that
![]() $F({\mathbb D}_{\rho _1})\supseteq {\mathbb D}_{\sigma _1}$
, where
$F({\mathbb D}_{\rho _1})\supseteq {\mathbb D}_{\sigma _1}$
, where
Now, we prove the sharpness of
![]() $\rho _1$
and
$\rho _1$
and
![]() $\sigma _1$
. To this end, we consider the bi-analytic function
$\sigma _1$
. To this end, we consider the bi-analytic function
![]() $F_1(z)$
which is given by (2.2). It is easy to verify that
$F_1(z)$
which is given by (2.2). It is easy to verify that
![]() $F_1(z)$
satisfies the hypothesis of Theorem 2.1, and thus, we have that
$F_1(z)$
satisfies the hypothesis of Theorem 2.1, and thus, we have that
![]() $F_1(z)$
is univalent in
$F_1(z)$
is univalent in
![]() ${\mathbb D}_{\rho _1}$
, and
${\mathbb D}_{\rho _1}$
, and
![]() $F_1({\mathbb D}_{\rho _1}) \supseteq {\mathbb D}_{\sigma _1}$
.
$F_1({\mathbb D}_{\rho _1}) \supseteq {\mathbb D}_{\sigma _1}$
.
To show that the radius
![]() $\rho _1$
is sharp, we need to prove that
$\rho _1$
is sharp, we need to prove that
![]() $F_1(z)$
is not univalent in
$F_1(z)$
is not univalent in
![]() ${\mathbb D}_r$
for each
${\mathbb D}_r$
for each
![]() $r\in (\rho _1, 1]$
. In fact for the real differentiable function
$r\in (\rho _1, 1]$
. In fact for the real differentiable function
![]() $h_0(x)$
given above, we have
$h_0(x)$
given above, we have
 $$ \begin{align*} h_0'(x)=\frac{2\Lambda_1x^2-\Lambda_2(2\Lambda_1+\Lambda_2)x+\Lambda_2}{\Lambda_2-x}, \end{align*} $$
$$ \begin{align*} h_0'(x)=\frac{2\Lambda_1x^2-\Lambda_2(2\Lambda_1+\Lambda_2)x+\Lambda_2}{\Lambda_2-x}, \end{align*} $$
which is continuous and strictly decreasing on
![]() $[0, 1]$
with
$[0, 1]$
with
![]() $h_0'(\rho _1)=0$
. It follows that
$h_0'(\rho _1)=0$
. It follows that
![]() $h_0'(x)=0$
for
$h_0'(x)=0$
for
![]() $x\in [0, 1]$
if and only if
$x\in [0, 1]$
if and only if
![]() $x=\rho _1$
. So
$x=\rho _1$
. So
![]() $h_0(x)$
is strictly increasing on
$h_0(x)$
is strictly increasing on
![]() $[0, \rho _1)$
and strictly decreasing on
$[0, \rho _1)$
and strictly decreasing on
![]() $[\rho _1, 1]$
. Since
$[\rho _1, 1]$
. Since
![]() $h_0(0)=0$
, there is a unique real
$h_0(0)=0$
, there is a unique real
![]() $\rho _1'\in (\rho _1, 1]$
such that
$\rho _1'\in (\rho _1, 1]$
such that
![]() $h_0(\rho _1')=0$
if
$h_0(\rho _1')=0$
if
![]() $h_0(1)\leq 0$
, and
$h_0(1)\leq 0$
, and
For every fixed
![]() $r\in (\rho _1, 1]$
, set
$r\in (\rho _1, 1]$
, set
![]() $x_1=\rho _1+\varepsilon $
, where
$x_1=\rho _1+\varepsilon $
, where
 $$ \begin{align*} \varepsilon=\left\{ \begin{array}{lll} \displaystyle\min\left\{\frac{r-\rho_1}{2}, \frac{\rho_1'-\rho_1}{2}\right\}, && \mbox{ if } h_0(1)\leq 0,\\ \displaystyle \frac{r-\rho_1}{2}, && \mbox{ if } h_0(1)>0. \end{array} \right. \end{align*} $$
$$ \begin{align*} \varepsilon=\left\{ \begin{array}{lll} \displaystyle\min\left\{\frac{r-\rho_1}{2}, \frac{\rho_1'-\rho_1}{2}\right\}, && \mbox{ if } h_0(1)\leq 0,\\ \displaystyle \frac{r-\rho_1}{2}, && \mbox{ if } h_0(1)>0. \end{array} \right. \end{align*} $$
By the mean value theorem, there is a unique
![]() $\delta \in (0, \rho _1)$
such that
$\delta \in (0, \rho _1)$
such that
![]() $x_2:=\rho _1-\delta \in (0, \rho _1)$
and
$x_2:=\rho _1-\delta \in (0, \rho _1)$
and
![]() $h_0(x_1)=h_0(x_2)$
.
$h_0(x_1)=h_0(x_2)$
.
Let
![]() $z_1=x_1$
and
$z_1=x_1$
and
![]() $z_2=x_2$
. Then
$z_2=x_2$
. Then
![]() $z_1,\ z_2\in {\mathbb D}_r$
with
$z_1,\ z_2\in {\mathbb D}_r$
with
![]() $z_1\neq z_2$
and observe that
$z_1\neq z_2$
and observe that
Hence,
![]() $F_1$
is not univalent in the disk
$F_1$
is not univalent in the disk
![]() ${\mathbb D}_r$
for each
${\mathbb D}_r$
for each
![]() $r\in (\rho _2, 1]$
, and thus, the radius
$r\in (\rho _2, 1]$
, and thus, the radius
![]() $\rho _1$
is sharp.
$\rho _1$
is sharp.
Finally, note that
![]() $F_1(0)=0$
and picking up
$F_1(0)=0$
and picking up
![]() $z'=\rho _1\in \partial {\mathbb D}_{\rho _1}$
, by (2.2), (4.2), and (4.3), we have
$z'=\rho _1\in \partial {\mathbb D}_{\rho _1}$
, by (2.2), (4.2), and (4.3), we have
Hence, the radius
![]() $\sigma _1$
of the schlicht disk is also sharp.
$\sigma _1$
of the schlicht disk is also sharp.
4.2 Proof of Theorem 2.2
The assumption on H, namely,
![]() $H\in {\mathcal B}_1\cap {\mathcal A}$
, clearly gives that
$H\in {\mathcal B}_1\cap {\mathcal A}$
, clearly gives that
![]() $H(z)\equiv z$
in
$H(z)\equiv z$
in
![]() ${\mathbb D}$
(by Schwarz’s lemma). Thus, F reduces to the form
${\mathbb D}$
(by Schwarz’s lemma). Thus, F reduces to the form
![]() $F(z)=\bar {z} G(z)+z$
.
$F(z)=\bar {z} G(z)+z$
.
Now, we prove F is univalent in the disk
![]() ${\mathbb D}_{\rho _1}$
. To this end, for any
${\mathbb D}_{\rho _1}$
. To this end, for any
![]() $z_1,z_2\in {\mathbb D}_r\, (0<r<\rho _2)$
with
$z_1,z_2\in {\mathbb D}_r\, (0<r<\rho _2)$
with
![]() $z_1\neq z_2$
, by the condition
$z_1\neq z_2$
, by the condition
![]() $G(0)=0$
and
$G(0)=0$
and
![]() $|G'(z)|\leq \Lambda $
for all
$|G'(z)|\leq \Lambda $
for all
![]() $z\in {\mathbb D}$
, and (4.1), it follows that
$z\in {\mathbb D}$
, and (4.1), it follows that
![]() $|G(z)|\leq \Lambda |z|$
in
$|G(z)|\leq \Lambda |z|$
in
![]() ${\mathbb D}$
. Consequently,
${\mathbb D}$
. Consequently,
 $$ \begin{align*} |F(z_1)-F(z_2)|&\geq |z_1-z_2| -\bigg|\int_{[z_1,z_2]}\bar{z}G'(z)dz+G(z)d\bar{z}\bigg|\\ &\geq |z_1-z_2|(1-2\Lambda r)>0, \end{align*} $$
$$ \begin{align*} |F(z_1)-F(z_2)|&\geq |z_1-z_2| -\bigg|\int_{[z_1,z_2]}\bar{z}G'(z)dz+G(z)d\bar{z}\bigg|\\ &\geq |z_1-z_2|(1-2\Lambda r)>0, \end{align*} $$
which proves the univalency of F in the disk
![]() ${\mathbb D}_{\rho _2}$
, where
${\mathbb D}_{\rho _2}$
, where
![]() $\rho _2$
is given in the statement of the theorem.
$\rho _2$
is given in the statement of the theorem.
Noticing that
![]() $F(0)=0$
, for any
$F(0)=0$
, for any
![]() $z=\rho _2 e^{i\theta }\in \partial {\mathbb D}_{\rho _2}$
, we have
$z=\rho _2 e^{i\theta }\in \partial {\mathbb D}_{\rho _2}$
, we have
Hence,
![]() $F({\mathbb D}_{\rho _2})$
contains a schlicht disk
$F({\mathbb D}_{\rho _2})$
contains a schlicht disk
![]() ${\mathbb D}_{\sigma _2}$
.
${\mathbb D}_{\sigma _2}$
.
Finally, for
![]() $F_2(z)=\Lambda |z|^2+z$
, a direct computation verifies that
$F_2(z)=\Lambda |z|^2+z$
, a direct computation verifies that
![]() $\rho _2$
and
$\rho _2$
and
![]() $\sigma _2$
are sharp. This completes the proof.
$\sigma _2$
are sharp. This completes the proof.
![]() $\Box $
$\Box $
4.3 Proof of Theorem 2.6
As
![]() $G\in \mathcal {B}_{M_1}\cap \mathcal {A}$
and
$G\in \mathcal {B}_{M_1}\cap \mathcal {A}$
and
![]() $H\in \mathcal {B}_{M_2}\cap \mathcal {A}$
by assumption, we may write
$H\in \mathcal {B}_{M_2}\cap \mathcal {A}$
by assumption, we may write
 $$ \begin{align*} G(z)=\sum\limits_{n=1}^\infty a_n z^n ~\mbox{ and }~ H(z)=\sum\limits_{n=1}^\infty b_n z^n, \end{align*} $$
$$ \begin{align*} G(z)=\sum\limits_{n=1}^\infty a_n z^n ~\mbox{ and }~ H(z)=\sum\limits_{n=1}^\infty b_n z^n, \end{align*} $$
where
![]() $a_1=b_1=1$
, and it follows from Lemma 3.3 that
$a_1=b_1=1$
, and it follows from Lemma 3.3 that
We first prove that F is univalent in the disk
![]() ${\mathbb D}_{\rho _3}$
, where
${\mathbb D}_{\rho _3}$
, where
![]() $\rho _3$
is defined by (2.3). Indeed, for all
$\rho _3$
is defined by (2.3). Indeed, for all
![]() $z_1,z_2\in {\mathbb D}_r\, (0<r<\rho _3$
,
$z_1,z_2\in {\mathbb D}_r\, (0<r<\rho _3$
,
![]() $z_1\neq z_2)$
, we see that (with
$z_1\neq z_2)$
, we see that (with
![]() $\gamma =[z_1,z_2]$
)
$\gamma =[z_1,z_2]$
)
 $$ \begin{align*} &\quad \ |F(z_2)-F(z_1)|=\left|\int_{\gamma}F_z(z)dz+F_{\bar{z}}(z)d\bar{z}\right|\nonumber\\ &\geq \bigg|\int_{\gamma}H'(0)dz\bigg|-\bigg|\int_{\gamma}(H'(z)-H'(0))dz\bigg| -\bigg|\int_{\gamma}\bar{z}G'(z)dz+G(z)d\bar{z}\bigg|\\\\ &\geq |z_1-z_2|\bigg[1-\sum\limits_{n=2}^\infty n|b_n|r^{n-1}-\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\bigg]\nonumber\\ &\geq |z_1-z_2|\bigg [1-\Big(M_2-\frac{1}{M_2}\Big)\sum\limits_{n=2}^\infty nr^{n-1}-\Big(M_1-\frac{1}{M_1}\Big)\sum\limits_{n=2}^\infty (n+1)r^{n}-2r\bigg ]\nonumber\\ &= |z_1-z_2|\Big [1-\Big(M_2-\frac{1}{M_2}\Big)\frac{2r-r^2}{(1-r)^2}-\Big(M_1-\frac{1}{M_1}\Big)\frac{(3-2r)r^2}{(1-r)^2}-2r\Big ]>0.\nonumber \end{align*} $$
$$ \begin{align*} &\quad \ |F(z_2)-F(z_1)|=\left|\int_{\gamma}F_z(z)dz+F_{\bar{z}}(z)d\bar{z}\right|\nonumber\\ &\geq \bigg|\int_{\gamma}H'(0)dz\bigg|-\bigg|\int_{\gamma}(H'(z)-H'(0))dz\bigg| -\bigg|\int_{\gamma}\bar{z}G'(z)dz+G(z)d\bar{z}\bigg|\\\\ &\geq |z_1-z_2|\bigg[1-\sum\limits_{n=2}^\infty n|b_n|r^{n-1}-\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\bigg]\nonumber\\ &\geq |z_1-z_2|\bigg [1-\Big(M_2-\frac{1}{M_2}\Big)\sum\limits_{n=2}^\infty nr^{n-1}-\Big(M_1-\frac{1}{M_1}\Big)\sum\limits_{n=2}^\infty (n+1)r^{n}-2r\bigg ]\nonumber\\ &= |z_1-z_2|\Big [1-\Big(M_2-\frac{1}{M_2}\Big)\frac{2r-r^2}{(1-r)^2}-\Big(M_1-\frac{1}{M_1}\Big)\frac{(3-2r)r^2}{(1-r)^2}-2r\Big ]>0.\nonumber \end{align*} $$
This implies
![]() $F(z_1)\neq F(z_2)$
, which proves the univalency of F in the disk
$F(z_1)\neq F(z_2)$
, which proves the univalency of F in the disk
![]() ${\mathbb D}_{\rho _3}$
.
${\mathbb D}_{\rho _3}$
.
Next, we prove that
![]() $F({\mathbb D}_{\rho _3}) \supseteq {\mathbb D}_{\sigma _3}$
, where
$F({\mathbb D}_{\rho _3}) \supseteq {\mathbb D}_{\sigma _3}$
, where
![]() $\sigma _3$
is as in the statement. Indeed, note that
$\sigma _3$
is as in the statement. Indeed, note that
![]() $F(0)=0$
and for any
$F(0)=0$
and for any
![]() $z'\in \partial {\mathbb D}_{\rho _3}$
with
$z'\in \partial {\mathbb D}_{\rho _3}$
with
![]() $w'=F(z')\in F(\partial {\mathbb D}_{\rho _3})$
, it follows from (4.4) that
$w'=F(z')\in F(\partial {\mathbb D}_{\rho _3})$
, it follows from (4.4) that
 $$ \begin{align*} |w'|&= \big|\bar{z'}G(z')+H(z')\big|\geq |H(z')|-\rho_3 |G(z')|\\ &\geq |z'|-\sum\limits_{n=2}^\infty |b_n|\,|z'|^{n}-\rho_3\sum\limits_{n=1}^\infty |a_n|\,|z'|^{n}\\ &\geq \rho_3-\rho_3^2-\Big(M_2-\frac{1}{M_2}\Big)\frac{\rho_3^2}{1-\rho_3}-\Big(M_1-\frac{1}{M_1}\Big)\frac{\rho_3^3}{1-\rho_3}=\sigma_3, \end{align*} $$
$$ \begin{align*} |w'|&= \big|\bar{z'}G(z')+H(z')\big|\geq |H(z')|-\rho_3 |G(z')|\\ &\geq |z'|-\sum\limits_{n=2}^\infty |b_n|\,|z'|^{n}-\rho_3\sum\limits_{n=1}^\infty |a_n|\,|z'|^{n}\\ &\geq \rho_3-\rho_3^2-\Big(M_2-\frac{1}{M_2}\Big)\frac{\rho_3^2}{1-\rho_3}-\Big(M_1-\frac{1}{M_1}\Big)\frac{\rho_3^3}{1-\rho_3}=\sigma_3, \end{align*} $$
which implies that
![]() $F({\mathbb D}_{\rho _3})\supseteq {\mathbb D}_{\sigma _3}$
.
$F({\mathbb D}_{\rho _3})\supseteq {\mathbb D}_{\sigma _3}$
.
![]() $\Box $
$\Box $
4.4 Proof of Theorem 2.10
We apply Lemmas 3.3 and 3.4. Now, by the assumption and the method of proof of Theorem 2.6, the inequalities in (4.4) hold, and thus, we have
 $$ \begin{align*} &\quad \sum\limits_{n=2}^\infty n|b_n|r^{n-1}+\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\\ &\leq \Big(M_2-\frac{1}{M_2}\Big)\sum\limits_{n=2}^\infty nr^{n-1}+\Big(M_1-\frac{1}{M_1}\Big)\sum\limits_{n=2}^\infty (n+1)r^{n}+2r\leq 1 \end{align*} $$
$$ \begin{align*} &\quad \sum\limits_{n=2}^\infty n|b_n|r^{n-1}+\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\\ &\leq \Big(M_2-\frac{1}{M_2}\Big)\sum\limits_{n=2}^\infty nr^{n-1}+\Big(M_1-\frac{1}{M_1}\Big)\sum\limits_{n=2}^\infty (n+1)r^{n}+2r\leq 1 \end{align*} $$
for
![]() $r\leq \rho _3$
. Hence, the desired conclusion of Theorem 2.10 follows from Lemma 3.4.
$r\leq \rho _3$
. Hence, the desired conclusion of Theorem 2.10 follows from Lemma 3.4.
![]() $\Box $
$\Box $
Conflict of Interests
The authors declare that they have no conflict of interests, regarding the publication of this article.
Data Availability Statement
The authors declare that this research is purely theoretical and does not associate with any data.