The pencil of quartic curves

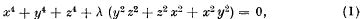
where x, y, z are homogeneous coordinates in a plane, was encountered by Ciani [Palermo Rendiconli, Vol. 13, 1899] in his search for plane quartic curves that were invariant under harmonic inversions. If x, y, z undergo any permutation the ternary quartic form on the left of (1) is not altered; nor is it altered if any, or all, of x, y, z be multiplied by −1. There thus arises an octahedral group G of ternary collineations for which every curve of the pencil is invariant.

Since (1) may also be written

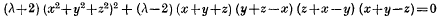
the four lines

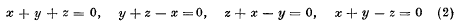
are, as Ciani pointed out, bitangents, at their intersections with the conic C whose equation is x2 + y2 + z2 = 0, to every quartic of the pencil. The 16 base points of the pencil are thus all accounted for—they consist of these eight contacts counted twice—and this set of points must of course be invariant under G. Indeed the 4! collineations of G are precisely those which give rise to the different permutations of the four lines (2), a collineation in a plane being determined when any four non-concurrent lines and the four lines which are to correspond to them are given. The quadrilateral formed by the lines (2) will be called q.