Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-06-12T01:02:24.439Z Has data issue: false hasContentIssue false
  • English
  • Français

Some problems of non-associative combinations (2)

Published online by Cambridge University Press:  31 October 2008

A. Erdelyi  and
I. M. H. Etherington
I. M. H. Etherington
Affiliation:
University College, Swansea
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

§ 1. The preceding Note has shown the connection between the partition of a convex polygon by non-crossing diagonals and the insertion of brackets in a product, the latter being more commonly represented by the construction of a tree. It was shown that the enumeration of these entities leads to a generating function y = f(x) which satisfies an algebraic equation of the type

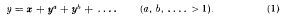
In simple cases, the solution of the equation was found as a power series in x, the coefficient An of xn giving the required number of partitions of an (n + 1)-gon.

Type
Research Article
Information
Edinburgh Mathematical Notes , Volume 32 , January 1940 , pp. vii - xii
Copyright
Copyright © Edinburgh Mathematical Society 1940

References

1 See e.g. Birkeland, , several notes in Comptes rendus, 32 (1920) and 172 (1921)Google Scholar; Belardinelli, , Annali di Mat. (3), 32 (1920), 251Google Scholar, Rend, de Lincei (5), 32 (1920), 208Google Scholar, Rend, di Palermo, 32 (1922), 463Google Scholar; Mayr, , Monatshefte für Math, und Phys., 32 (1937), 280 and 47 (1938), 164Google Scholar; Mellin, , Ann. Acad. Sci. Fenn. (A) 32 (1914–1915), Nos. 7 and 8.Google Scholar

2 Cf. Whittaker, and Watson, , Modern Analysis (1927), §7.32.Google Scholar

1 Lamé, Catalan, Rodrigues, Binet, Journ. de Math., 1838–1839.Google Scholar