Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-19T11:31:51.088Z Has data issue: false hasContentIssue false
  • English
  • Français

On invariant holonomies between centers

Part of: Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  08 May 2024

RADU SAGHIN Open the ORCID record for RADU SAGHIN [Opens in a new window]
RADU SAGHIN*
Affiliation:
Instituto de Matemática, Pontificia Universidad Católica de Valparaíso, Blanco Viel 596, Cerro Barón, Valparaíso, Chile
*
e-mail: radu.saghin@pucv.cl
Get access Rights & Permissions [Opens in a new window]

Abstract

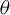We prove that for $C^{1+\theta }$, $\theta $-bunched, dynamically coherent partially hyperbolic diffeomorphisms, the stable and unstable holonomies between center leaves are $C^1$, and the derivative depends continuously on the points and on the map. Also for $C^{1+\theta }$, $\theta $-bunched partially hyperbolic diffeomorphisms, the derivative cocycle restricted to the center bundle has invariant continuous holonomies which depend continuously on the map. This generalizes previous results by Pugh, Shub, and Wilkinson; Burns and Wilkinson; Brown; Obata; Avila, Santamaria, and Viana; and Marin.

Keywords

partially hyperbolic diffeomorphismsinvariant foliationsholonomy

MSC classification

Primary: 37D30: Partially hyperbolic systems and dominated splittings
Secondary: 37D10: Invariant manifold theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 20
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A., Santamaria, J. and Viana, M.. Holonomy invariance: rough regularity and applications to Lyapunov exponents. Astérisque 358 (2013), 13–74.Google Scholar
Brown, A.. Smoothness of stable holonomies inside center-stable manifolds. Ergod. Th. & Dynam. Sys. 42(12) (2022), 3593–3618.CrossRefGoogle Scholar
Burns, K. and Wilkinson, A.. A Note on Stable Holonomy between Centers (preliminary version). Notes on A. Wilkinson’s personal webpage, 2005. Available at: https://www.math.uchicago.edu/~wilkinso/papers/c1hol0611.pdf Google Scholar
Burns, K. and Wilkinson, A.. On the ergodicity of partially hyperbolic systems. Ann. of Math. (2) 171(1) (2010), 451–489.CrossRefGoogle Scholar
Crovisier, S., Obata, D. and Poletti, M.. Uniqueness of $u$ -Gibbs measures for hyperbolic skew products on ${\mathrm{T}}^4$ . Preprint, 2022, arXiv:2209.09151.Google Scholar
Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer, Berlin, 1977.CrossRefGoogle Scholar
Kalinin, B. and Sadovskaya, V.. Cocycles with one exponent over partially hyperbolic systems. Geom. Dedicata 167 (2013), 167–188.CrossRefGoogle Scholar
Kalinin, B. and Sadovskaya, V.. Holonomies and cohomology for cocycles over partially hyperbolic diffeomorphisms. Discrete Contin. Dyn. Syst. 36(1) (2016), 245–259.CrossRefGoogle Scholar
Leguil, M. and Piñeyrúa, L.. Accessibility for dynamically coherent partially hyperbolic diffeomorphisms with 2D center. Preprint, 2022, arXiv:2112.12762.Google Scholar
Liang, C., Marin, K. and Yang, J.. Lyapunov exponents of partially hyperbolic volume preserving maps with 2-dimensional center bundle. Ann. Inst. H. Poincaré Anal. Non Linéaire 35(6) (2018), 1687–1706.CrossRefGoogle Scholar
Liang, C., Marin, K. and Yang, J.. ${C}^1$ -openness of non-uniform hyperbolic diffeomorphisms with bounded ${C}^2$ norm. Ergod. Th. & Dynam. Sys. 40(11) (2020), 3078–3104.CrossRefGoogle Scholar
Liang, C., Saghin, R., Yang, F. and Yang, J.. Shub’s example revisited. Preprint, 2023, arXiv:2303.17775.Google Scholar
Marin, K.. ${C}^r$ -density of (non-uniform) hyperbolicity in partially hyperbolic symplectic diffeomorphisms. Comment. Math. Helv. 91(2) (2016), 357–396.CrossRefGoogle Scholar
Obata, D.. On the holonomies of strong stable foliations. Notes on D. Obata’s personal webpage, 2018.Google Scholar
Obata, D.. Open sets of partially hyperbolic skew products having a unique SRB measure. Adv. Math. 427 (2023), Paper No. 109136.Google Scholar
Pugh, C., Shub, M. and Wilkinson, A.. Partial differentiability of invariant splittings. J. Stat. Phys. 114(3–4) (2004), 891–921.CrossRefGoogle Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A. and Ures, R.. Accessibility and stable ergodicity for partially hyperbolic diffeomorphisms with 1D-center bundle. Invent. Math. 172(2) (2008), 353–381.CrossRefGoogle Scholar