Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-02T18:43:01.761Z Has data issue: false hasContentIssue false
  • English
  • Français

Simple groups of dynamical origin

Published online by Cambridge University Press:  17 August 2017

V. NEKRASHEVYCH
V. NEKRASHEVYCH*
Affiliation:
Texas A&M University, Mathematics, College Station, Texas 77843-3368, USA email nekrash@math.tamu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

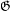We associate with every étale groupoid $\mathfrak{G}$ two normal subgroups 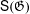$\mathsf{S}(\mathfrak{G})$ and 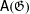$\mathsf{A}(\mathfrak{G})$ of the topological full group of 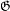$\mathfrak{G}$, which are analogs of the symmetric and alternating groups. We prove that if 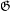$\mathfrak{G}$ is a minimal groupoid of germs (e.g., of a group action), then 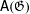$\mathsf{A}(\mathfrak{G})$ is simple and is contained in every non-trivial normal subgroup of the full group. We show that if 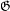$\mathfrak{G}$ is expansive (e.g., is the groupoid of germs of an expansive action of a group), then 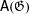$\mathsf{A}(\mathfrak{G})$ is finitely generated. We also show that 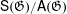$\mathsf{S}(\mathfrak{G})/\mathsf{A}(\mathfrak{G})$ is a quotient of 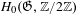$H_{0}(\mathfrak{G},\mathbb{Z}/2\mathbb{Z})$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 3 , March 2019 , pp. 707 - 732
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bellissard, J., Herrmann, D. J. L. and Zarrouati, M.. Hulls of aperiodic solids and gap labeling theorems. Directions in Mathematical Quasicrystals (CRM Monograph Series, 13) . Eds. Baake, M. and Moody, R. V.. American Mathematical Society, Providence, RI, 2000, pp. 207–258.Google Scholar
Bellissard, J., Julien, A. and Savinien, J.. Tiling groupoids and Bratteli diagrams. Ann. Henri Poincaré 11(1–2) (2010), 69–99.Google Scholar
de Brujin, N. G.. Algebraic theory of Penrose’s non-periodic tilings of the plane I. Indag. Math. (N.S.) 43(1) (1981), 39–52.Google Scholar
Cannon, J. W., Floyd, W. I. and Parry, W. R.. Introductory notes on Richard Thompson groups. Enseign. Math. 42(2) (1996), 215–256.Google Scholar
Chornyi, M., Juschenko, K. and Nekrashevych, V.. On topological full groups of $\mathbb{Z}^{d}$ -actions. Preprint 2016 arXiv:1602.04255.Google Scholar
de Cornulier, Y.. Groupes pleins-topologiques (d’après Matui, Juschenko, Monod,…). Astérisque 361 (2014), 183–223, Exp. No. 1064, viii.Google Scholar
D’Angeli, D., Donno, A., Matter, M. and Smirnova-Nagnibeda, T.. Schreier graphs of the basilica group. J. Mod. Dyn. 4(1) (2010), 139–177.Google Scholar
Giordano, T., Putnam, I. F. and Skau, C. F.. Full groups of Cantor minimal systems. Israel J. Math. 111 (1999), 285–320.Google Scholar
Guba, V. and Sapir, M.. Diagram Groups (Memoirs of the American Mathematical Society, 620) . American Mathematical Society, Providence, RI, 1997.Google Scholar
Haefliger, A.. Foliations and compactly generated pseudogroups. Foliations: Geometry and Dynamics (Warsaw, 2000). World Scientific, River Edge, NJ, 2002, pp. 275–295.Google Scholar
Kellendonk, J. and Lawson, M. V.. Tiling semigroups. J. Algebra 224(1) (2000), 140–150.Google Scholar
Kellendonk, J. and Putnam, I. F.. Tilings, C ∗ -algebras, and K-theory. Directions in Mathematical Quasicrystals (CRM Monograph Series, 13) . Ed. Baake, M. et al. . American Mathematical Society, Providence, RI, 2000, pp. 177–206.Google Scholar
Krieger, W.. On a dimension for a class of homeomorphism groups. Math. Ann. 252(2) (1979–1980), 87–95.Google Scholar
Lavrenyuk, Y. and Nekrashevych, V.. On classification of inductive limits of direct products of alternating groups. J. Lond. Math. Soc. 75(1) (2007), 146–162.Google Scholar
Leinen, F. and Puglisi, O.. Diagonal limits of finite alternating groups: confined subgroups, ideals, and positive defined functions. Illinois J. Math. 47(1–2) (2003), 345–360.Google Scholar
Leinen, F. and Puglisi, O.. Some results concerning simple locally finite groups of 1-type. J. Algebra 287 (2005), 32–51.Google Scholar
Lodha, Y. and Moore, J. T.. A nonamenable finitely presented group of piecewise projective homeomorphisms. Groups Geom. Dyn. 10(1) (2016), 177–200.Google Scholar
Matui, H.. Some remarks on topological full groups of Cantor minimal systems. Internat. J. Math. 17(2) (2006), 231–251.Google Scholar
Matui, H.. Homology and topological full groups of étale groupoids on totally disconnected spaces. Proc. Lond. Math. Soc. (3) 104(1) (2012), 27–56.Google Scholar
Matui, H.. Topological full groups of one-sided shifts of finite type. J. reine angew. Math. 705 (2015), 35–84.Google Scholar
Matui, H.. Étale groupoids arising from products of shifts of finite type. Adv. Math. 303 (2016), 502–548.Google Scholar
Medynets, K.. Reconstruction of orbits of Cantor systems from full groups. Bull. Lond. Math. Soc. 43(6) (2011), 1104–1110.Google Scholar
Monod, N.. Groups of piecewise projective homeomorphisms. Proc. Natl. Acad. Sci. USA 110(12) (2013), 4524–4527.Google Scholar
Nekrashevych, V.. Cuntz–Pimsner algebras of group actions. J. Operator Theory 52(2) (2004), 223–249.Google Scholar
Nekrashevych, V.. Finitely presented groups associated with expanding maps. Preprint 2013arXiv:1312.5654, to appear.Google Scholar
Nekrashevych, V.. Hyperbolic groupoids and duality. Mem. Amer. Math. Soc. 237(1122) (2015), 108 pp.Google Scholar
Nekrashevych, V.. Growth of étale groupoids and simple algebras. Internat. J. Algebra Comput. 26(2) (2016), 375–397.Google Scholar
Rubin, M.. On the reconstruction of topological spaces from their groups of homeomorphisms. Trans. Amer. Math. Soc. 312(2) (1989), 487–538.Google Scholar