Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-09T09:11:12.697Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermodynamics of the Katok map

Published online by Cambridge University Press:  28 June 2017

Y. PESIN ,
S. SENTI  and
K. ZHANG
Y. PESIN
Affiliation:
Department of Mathematics, Pennsylvania State University, University Park, PA 16802, USA email pesin@math.psu.edu
S. SENTI
Affiliation:
Instituto de Matematica, Universidade Federal do Rio de Janeiro, CP 68 530, CEP 21945-970, R.J., Brazil email senti@im.ufrj.br
K. ZHANG
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario, Canada email kezhang@math.umd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We effect the thermodynamical formalism for the non-uniformly hyperbolic 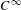$C^{\infty }$ map of the two-dimensional torus known as the Katok map [Katok. Bernoulli diffeomorphisms on surfaces. Ann. of Math. (2)110(3) 1979, 529–547]. It is a slow-down of a linear Anosov map near the origin and it is a local (but not small) perturbation. We prove the existence of equilibrium measures for any continuous potential function and obtain uniqueness of equilibrium measures associated to the geometric $t$-potential 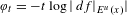$\unicode[STIX]{x1D711}_{t}=-t\log \mid df|_{E^{u}(x)}|$ for any 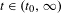$t\in (t_{0},\infty )$, 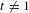$t\neq 1$, where 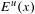$E^{u}(x)$ denotes the unstable direction. We show that 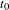$t_{0}$ tends to 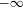$-\infty$ as the domain of the perturbation shrinks to zero. Finally, we establish exponential decay of correlations as well as the central limit theorem for the equilibrium measures associated to 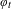$\unicode[STIX]{x1D711}_{t}$ for all values of 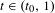$t\in (t_{0},1)$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 3 , March 2019 , pp. 764 - 794
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J., Denker, M. and Urbański, M.. Ergodic theory for Markov fibred systems and parabolic rational maps. Trans. Amer. Math. Soc. 337(2) (1993), 495–548.Google Scholar
Barbosa, E. P.. Formalismo termodinmico e estabilidade estatstica no desdobramento de tangncia homoclnica. PhD Thesis, IM-UFRJ, http://www.pgmat.im.ufrj.br/index.php/pt-br/teses-e-dissertacoes/teses/2013-1/33-18/file, 2013.Google Scholar
Barreira, L. and Pesin, Y. B.. Introduction to Smooth Ergodic Theory (Graduate Studies in Mathematics, 148) . American Mathematical Society, Providence, RI, 2013.Google Scholar
Climenhaga, V. and Pesin, Ya.. Building thermodynamics for non-uniformly hyperbolic maps. Arnold Math. J. 3(1) (2017), 37–82.Google Scholar
Hu, H.. Decay of correlations for piecewise smooth maps with indifferent fixed points. Ergod. Th. & Dynam. Sys. 24(2) (2004), 495–524.Google Scholar
Katok, A.. Bernoulli diffeomorphisms on surfaces. Ann. of Math. (2) 110(3) (1979), 529–547.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, New York, 1995.Google Scholar
Lopes, A. O.. The zeta function, nondifferentiability of pressure, and the critical exponent of transition. Adv. Math. 101(2) (1993), 133–165.Google Scholar
Leplaideur, R. and Rios, I.. Invariant manifolds and equilibrium states for non-uniformly hyperbolic horseshoes. Nonlinearity 19(11) (2006), 2667–2694.Google Scholar
Liverani, C., Saussol, B. and Vaienti, S.. A probabilistic approach to intermittency. Ergod. Th. & Dynam. Sys. 19(3) (1999), 671–685.Google Scholar
Pomeau, Y. and Manneville, P.. Intermittent transition to turbulence in dissipative dynamical systems. Comm. Math. Phys. 74(2) (1980), 189–197.Google Scholar
Pesin, Y. and Senti, S.. Thermodynamical formalism associated with inducing schemes for one-dimensional maps. Mosc. Math. J. 5(3) (2005), 669–678.Google Scholar
Pesin, Y. and Senti, S.. Equilibrium measures for maps with inducing schemes. J. Mod. Dyn. 2(3) (2008), 397–430.Google Scholar
Prellberg, T. and Slawny, J.. Maps of intervals with indifferent fixed points: thermodynamic formalism and phase transitions. J. Stat. Phys. 66(1–2) (1992), 503–514.Google Scholar
Pesin, Y., Samuel, S. and Shahidi, F.. Area preserving surface diffeomorphisms with polynomial decay rate are ubiquitous. Preprint, 2017.Google Scholar
Pesin, Ya. B., Senti, S. and Zhang, K.. Thermodynamics of towers of hyperbolic type. Trans Amer. Math. Soc. (2016).Google Scholar
Pollicott, M. and Weiss, H.. Multifractal analysis of Lyapunov exponent for continued fraction and Manneville–Pomeau transformations and applications to Diophantine approximation. Comm. Math. Phys. 207(1) (1999), 145–171.Google Scholar
Pollicott, M. and Yuri, M.. Statistical properties of maps with indifferent periodic points. Comm. Math. Phys. 217(3) (2001), 503–520.Google Scholar
Pesin, Y. and Zhang, K.. Phase transitions for uniformly expanding maps. J. Stat. Phys. 122(6) (2006), 1095–1110.Google Scholar
Sarig, O. M.. Phase transitions for countable Markov shifts. Comm. Math. Phys. 217(3) (2001), 555–577.Google Scholar
Sarig, O.. Subexponential decay of correlations. Invent. Math. 150(3) (2002), 629–653.Google Scholar
Senti, S. and Takahasi, H.. Equilibrium measures for the Hénon map at the first bifurcation. Nonlinearity 26(6) (2013), 1719–1741.Google Scholar
Senti, S. and Takahasi, H.. Equilibrium measures for the Hénon map at the first bifurcation: uniqueness and geometric/statistical properties. Ergod. Th. & Dynam. Sys. 36 (2016), 215–255.Google Scholar
Shahidi, F. and Zelerowicz, A.. Ergodic properties of equilibrium measures for young diffeomorphisms. Preprint, 2017.Google Scholar
Young, L.-S.. Statistical properties of dynamical systems with some hyperbolicity. Ann. of Math. (2) 147(3) (1998), 585–650.Google Scholar
Young, L.-S.. Recurrence times and rates of mixing. Israel J. Math. 110 (1999), 153–188.Google Scholar