No CrossRef data available.
Article contents
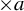 $\times a$ and
$\times a$ and 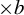 $\times b$ empirical measures, the irregular set and entropy
$\times b$ empirical measures, the irregular set and entropy
Published online by Cambridge University Press: 15 August 2023
Abstract
For integers a and 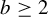 $b\geq 2$, let
$b\geq 2$, let 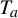 $T_a$ and
$T_a$ and 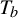 $T_b$ be multiplication by a and b on
$T_b$ be multiplication by a and b on 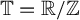 $\mathbb {T}=\mathbb {R}/\mathbb {Z}$. The action on
$\mathbb {T}=\mathbb {R}/\mathbb {Z}$. The action on 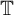 $\mathbb {T}$ by
$\mathbb {T}$ by 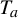 $T_a$ and
$T_a$ and 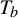 $T_b$ is called
$T_b$ is called 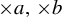 $\times a,\times b$ action and it is known that, if a and b are multiplicatively independent, then the only
$\times a,\times b$ action and it is known that, if a and b are multiplicatively independent, then the only 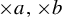 $\times a,\times b$ invariant and ergodic measure with positive entropy of
$\times a,\times b$ invariant and ergodic measure with positive entropy of 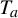 $T_a$ or
$T_a$ or 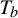 $T_b$ is the Lebesgue measure. However, it is not known whether there exists a non-trivial
$T_b$ is the Lebesgue measure. However, it is not known whether there exists a non-trivial 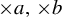 $\times a,\times b$ invariant and ergodic measure. In this paper, we study the empirical measures of
$\times a,\times b$ invariant and ergodic measure. In this paper, we study the empirical measures of 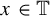 $x\in \mathbb {T}$ with respect to the
$x\in \mathbb {T}$ with respect to the 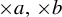 $\times a,\times b$ action and show that the set of x such that the empirical measures of x do not converge to any measure has Hausdorff dimension one and the set of x such that the empirical measures can approach a non-trivial
$\times a,\times b$ action and show that the set of x such that the empirical measures of x do not converge to any measure has Hausdorff dimension one and the set of x such that the empirical measures can approach a non-trivial 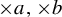 $\times a,\times b$ invariant measure has Hausdorff dimension zero. Furthermore, we obtain some equidistribution result about the
$\times a,\times b$ invariant measure has Hausdorff dimension zero. Furthermore, we obtain some equidistribution result about the 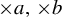 $\times a,\times b$ orbit of x in the complement of a set of Hausdorff dimension zero.
$\times a,\times b$ orbit of x in the complement of a set of Hausdorff dimension zero.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press





