Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-06-11T12:03:08.827Z Has data issue: false hasContentIssue false
  • English
  • Français

A simple proof of the characterization of functions of low Aviles Giga energy on a ball via regularity

Published online by Cambridge University Press:  13 April 2011

Andrew Lorent
Andrew Lorent*
Affiliation:
Mathematics Department, University of Cincinnati, 2600 Clifton Ave., Cincinnati, Ohio 45221, USA. lorentaw@uc.edu
Get access

Abstract

The Aviles Giga functional is a well known second order functional that forms a model for blistering and in a certain regime liquid crystals, a related functional models thin magnetized films. 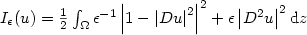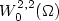Given Lipschitz domain Ω ⊂ ℝ2 the functional is \hbox{$I_{\ep}(u)=\frac{1}{2}\int_{\Omega} \ep^{-1}\lt|1-\lt|Du\rt|^2\rt|^2+\ep\lt|D^2 u\rt|^2 {\rm d}z$}Iϵ(u)=12∫Ωϵ-11−Du22+ϵD2u2dz where u belongs to the subset of functions in \hbox{$W^{2,2}_{0}(\Omega)$}W02,2(Ω) whose gradient (in the sense of trace) satisfies Du(x)·ηx = 1 where ηx is the inward pointing unit normal to ∂Ω at x. In [Ann. Sc. Norm. Super. Pisa Cl. Sci. 1 (2002) 187–202] Jabin et al. characterized a class of functions which includes all limits of sequences \hbox{$u_n\in W^{2,2}_0(\Omega)$}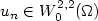un∈W02,2(Ω) with Iϵn(un) → 0 as ϵn → 0. A corollary to their work is that if there exists such a sequence (un) for a bounded domain Ω, then Ω must be a ball and (up to change of sign) u: = limn → ∞un = dist(·,∂Ω). Recently [Lorent, Ann. Sc. Norm. Super. Pisa Cl. Sci. (submitted), http://arxiv.org/abs/0902.0154v1] we provided a quantitative generalization of this corollary over the space of convex domains using ‘compensated compactness’ inspired calculations of DeSimone et al. [Proc. Soc. Edinb. Sect. A 131 (2001) 833–844]. In this note we use methods of regularity theory and ODE to provide a sharper estimate and a much simpler proof for the case where Ω = B1(0) without the requiring the trace condition on Du.

Keywords

Aviles Giga functional
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 18 , Issue 2 , April 2012 , pp. 383 - 400
Copyright
© EDP Sciences, SMAI, 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alouges, F., Riviere, T. and Serfaty, S., Neel and cross-tie wall energies for planar micromagnetic configurations. ESAIM : COCV 8 (2002) 31–68. Google Scholar
Ambrosio, L., Delellis, C. and Mantegazza, C., Line energies for gradient vector fields in the plane. Calc. Var. Partial Differential Equations 9 (1999) 327–355. Google Scholar
Ambrosio, L., Lecumberry, M. and Riviere, T., Viscosity property of minimizing micromagnetic configurations. Commun. Pure Appl. Math. 56 (2003) 681–688. Google Scholar
P. Aviles and Y. Giga, A mathematical problem related to the physical theory of liquid crystal configurations, in Miniconference on geometry and partial differential equations 2, Canberra (1986) 1–16, Proc. Centre Math. Anal. Austral. Nat. Univ. 12, Austral. Nat. Univ., Canberra (1987).
Aviles, P. and Giga, Y., The distance function and defect energy. Proc. Soc. Edinb. Sect. A 126 (1996) 923–938. Google Scholar
Aviles, P. and Giga, Y., On lower semicontinuity of a defect energy obtained by a singular limit of the Ginzburg-Landau type energy for gradient fields. Proc. Soc. Edinb. Sect. A 129 (1999) 1–17. Google Scholar
Carbou, G., Regularity for critical points of a nonlocal energy. Calc. Var. 5 (1997) 409–433. Google Scholar
S. Conti, A. DeSimone, S. Müller, R. Kohn and F. Otto, Multiscale modeling of materials – the role of analysis, in Trends in nonlinear analysis, Springer, Berlin (2003) 375–408.
DeSimone, A., Müller, S., Kohn, R. and Otto, F., A compactness result in the gradient theory of phase transitions. Proc. Soc. Edinb. Sect. A 131 (2001) 833–844. Google Scholar
DeSimone, A., Müller, S., Kohn, R. and Otto, F., A reduced theory for thin-film micromagnetics. Commun. Pure Appl. Math. 55 (2002) 1408–1460. Google Scholar
L.C. Evans, Partial differential equations, Graduate Studies in Mathematics 19. American Mathematical Society (1998).
L.C. Evans and R.F. Gariepy, Measure theory and fine properties of functions. Studies in Advanced Mathematics, CRC Press (1992).
Gioia, G. and Ortiz, M., The morphology and folding patterns of buckling-driven thin-film blisters. J. Mech. Phys. Solids 42 (1994) 531–559. Google Scholar
Hardt, R. and Kinderlehrer, D., Some regularity results in ferromagnetism. Commun. Partial Differ. Equ. 25 (2000) 1235–1258. Google Scholar
Ignat, R. and Otto, F., A compactness result in thin-film micromagnetics and the optimality of the Néel wall. J. Eur. Math. Soc. (JEMS) 10 (2008) 909–956. Google Scholar
Jabin, P., Otto, F. and Perthame, B., Line-energy Ginzburg-Landau models : zero-energy states. Ann. Sc. Norm. Super. Pisa Cl. Sci. 1 (2002) 187–202. Google Scholar
Jin, W. and Kohn, R.V., Singular perturbation and the energy of folds. J. Nonlinear Sci. 10 (2000) 355–390. Google Scholar
A. Lorent, A quantitative characterisation of functions with low Aviles Giga energy on convex domains. Ann. Sc. Norm. Super. Pisa Cl. Sci. (submitted). Available at http://arxiv.org/abs/0902.0154v1.
Riviere, T. and Serfaty, S., Limiting domain wall energy for a problem related to micromagnetics. Commun. Pure Appl. Math. 54 (2001) 294–338. Google Scholar
E.M. Stein, Singular integrals and differentiability properties of functions, Princeton Mathematical Series 30. Princeton University Press (1970).