Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-31T18:59:58.469Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Lie symmetries of characteristic function hierarchy in compressible turbulence

Part of: Basic methods in fluid mechanics Turbulence

Published online by Cambridge University Press:  11 April 2022

D.S. PRATURI Open the ORCID record for D.S. PRATURI [Opens in a new window] ,
D. PLÜMACHER  and
M. OBERLACK
D.S. PRATURI
Affiliation:
Chair of Fluid Dynamics, TU Darmstadt, 64287 Darmstadt, Germany emails: dspraturi@gmail.com; pluemacher@fdy.tu-darmstadt.de
D. PLÜMACHER
Affiliation:
Chair of Fluid Dynamics, TU Darmstadt, 64287 Darmstadt, Germany emails: dspraturi@gmail.com; pluemacher@fdy.tu-darmstadt.de
M. OBERLACK
Affiliation:
Chair of Fluid Dynamics, TU Darmstadt, 64287 Darmstadt, Germany emails: dspraturi@gmail.com; pluemacher@fdy.tu-darmstadt.de Center for Computational Engineering, TU Darmstadt, 64293 Darmstadt, Germany email: oberlack@fdy.tu-darmstadt.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We compute the Lie symmetries of characteristic function (CF) hierarchy of compressible turbulence, ignoring the effects of viscosity and heat conductivity. In the probability density function (PDF) hierarchy, a typical non-local nature is observed, which is naturally eliminated in the CF hierarchy. We observe that the CF hierarchy retains all the symmetries satisfied by compressible Euler equations. Broadly speaking, four types of symmetries can be discerned in the CF hierarchy: (i) symmetries corresponding to coordinate system invariance, (ii) scaling/dilation groups, (iii) projective groups and (iv) statistical symmetries, where the latter define measures of intermittency and non-gaussianity. As the multi-point CFs need to satisfy additional constraints such as the reduction condition, the projective symmetries are only valid for monatomic gases, that is, the specific heat ratio, 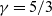$\gamma = 5/3$. The linearity of the CF hierarchy results in the statistical symmetries due to the superposition principle. For all of the symmetries, the global transformations of the CF and various key compressible statistics are also presented.

Keywords

Characteristic function hierarchycompressible turbulencesymmetry analysis

MSC classification

Primary: 76M60: Symmetry analysis, Lie group and algebra methods
Secondary: 76F50: Compressibility effects
Type
Papers
Information
European Journal of Applied Mathematics , Volume 34 , Special Issue 5: Symmetries and Differential Equations , October 2023 , pp. 913 - 935
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avsarkisov, V., Oberlack, M. & Hoyas, S. (2014) New scaling laws for turbulent Poiseuille flow with wall transpiration. J. Fluid Mech. 746, 99–122.CrossRefGoogle Scholar
Bluman, G. W. & Kumei, S. (1989) Symmetries and Differential Equations, Vol. 81, Springer Science & Business Media, New York.CrossRefGoogle Scholar
Cantwell, B. J. (2002) Introduction to Symmetry Analysis. Cambridge University Press, Cambridge, UK.Google Scholar
Farshchi, M. (1989) A probability density function closure model for compressible turbulent chemically reacting flows. In: 27th Aerospace Sciences Meeting, p. 390.CrossRefGoogle Scholar
Fox, R. L. (1975) Multipoint distribution function hierarchy for compressible turbulent flow. Phys. Fluids 18(10), 1245–1248.CrossRefGoogle Scholar
Ibragimov, N. H. (1995) CRC Handbook of Lie Group Analysis of Differential Equations, Vol. 1. CRC Press, Boca Raton, FL.Google Scholar
Kollmann, W. (1990) The pdf approach to turbulent flow. Theoret. Comput. Fluid Dyn. 1(5), 249–285.CrossRefGoogle Scholar
Lumley, J. L. (1970) Stochastic Tools in Turbulence. Academic Press, New York and London.Google Scholar
Lundgren, T. S. (1967) Distribution functions in the statistical theory of turbulence. Phys. Fluids 10(5), 969–975.CrossRefGoogle Scholar
Maple, (2019). Maplesoft, a division of Waterloo Maple Inc., Waterloo, Ontario.Google Scholar
Oberlack, M., Hoyas, S., Kraheberger, S. V., Alcántara-Ávila, F. & Laux, J. (2022) Turbulence statistics of arbitrary moments of wall-bounded shear flows: a symmetry approach. Phys. Rev. Lett. 128(2), 024502.CrossRefGoogle ScholarPubMed
Oberlack, M. & Rosteck, A. (2010) New statistical symmetries of the multi-point equations and its importance for turbulent scaling laws. Discrete Contin. Dyn. Syst.-S 3(3), 451.Google Scholar
Olver, P. J. (1986) Applications of Lie Groups to Differential Equations. Vol. 107. Springer Science & Business Media, New York.CrossRefGoogle Scholar
Ovsiannikov, L. V. (1982) Group Analysis of Differential Equations. Academic Press, New York.Google Scholar
Pope, S. B. (2000) Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Praturi, D. S., Plümacher, D. & Oberlack, M. (2020) The hierarchy of multi-point probability density functions and characteristic functions in compressible turbulence. Phys. Fluids 32(6), 066102.CrossRefGoogle Scholar
Sadeghi, H., Oberlack, M. & Gauding, M. (2018) On new scaling laws in a temporally evolving turbulent plane jet using Lie symmetry analysis and direct numerical simulation. J. Fluid Mech. 854, 233–260.CrossRefGoogle Scholar
Sadeghi, H. & Oberlack, M. (2020) New scaling laws of passive scalar with a constant mean gradient in decaying isotropic turbulence. J. Fluid Mech. 899, A10-1–A10-26.CrossRefGoogle Scholar
Sadeghi, H., Oberlack, M. & Gauding, M. (2021) New symmetry-induced scaling laws of passive scalar transport in turbulent plane jets. J. Fluid Mech. 919, A5-1–A5-27.CrossRefGoogle Scholar
Wacławczyk, M., Grebenev, V. N. & Oberlack, M. (2017) Lie symmetry analysis of the Lundgren–Monin–Novikov equations for multi-point probability density functions of turbulent flow. J. Phys. A Math. Theoret. 50(17), 175501.CrossRefGoogle Scholar
Wacławczyk, M., Staffolani, N., Oberlack, M., Rosteck, A., Wilczek, M. & Friedrich, R. (2014) Statistical symmetries of the Lundgren–Monin–Novikov hierarchy. Phys. Rev. E 90(1), 013022.CrossRefGoogle ScholarPubMed