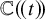1 Introduction
Given a smooth genus
![]() $g\geq 2$
algebraic curve C together with a point
$g\geq 2$
algebraic curve C together with a point
![]() $p \in C$
, there is a canonical null-homologous 1-cycle in its Jacobian
$p \in C$
, there is a canonical null-homologous 1-cycle in its Jacobian
![]() $\operatorname {\mathrm {Jac}}(C)$
obtained by taking the difference of the images of C under the two Abel–Jacobi maps
$\operatorname {\mathrm {Jac}}(C)$
obtained by taking the difference of the images of C under the two Abel–Jacobi maps
This is called the Ceresa cycle, and we denote it by
![]() $C - C^{-}$
. A landmark result of Ceresa in [Reference Ceresa6] is that this cycle, for a very general curve of genus
$C - C^{-}$
. A landmark result of Ceresa in [Reference Ceresa6] is that this cycle, for a very general curve of genus
![]() $g\geq 3$
, is nontrivial in the Griffiths group of null-homologous cycles modulo algebraic equivalence. Nevertheless, it is always trivial for hyperelliptic curves, and it has long been conjectured that these are the only curves with trivial Ceresa cycle [Reference Hain13, Question 8.5], [Reference Bisogno, Li, Litt and Srinivasan4, Remark 1.2]. Although several recent results [Reference Beauville1, Reference Beauville and Schoen2, Reference Bisogno, Li, Litt and Srinivasan4, Reference Lilienfeldt and Shnidman14] present nonhyperelliptic curves whose Ceresa cycles give rise to torsion classes in the Griffiths group, this problem remains open. The goal of this paper is to study hyperellipticity of tropical curves and graphs using cohomological invariants arising from the study of Ceresa triviality of algebraic curves defined over
$g\geq 3$
, is nontrivial in the Griffiths group of null-homologous cycles modulo algebraic equivalence. Nevertheless, it is always trivial for hyperelliptic curves, and it has long been conjectured that these are the only curves with trivial Ceresa cycle [Reference Hain13, Question 8.5], [Reference Bisogno, Li, Litt and Srinivasan4, Remark 1.2]. Although several recent results [Reference Beauville1, Reference Beauville and Schoen2, Reference Bisogno, Li, Litt and Srinivasan4, Reference Lilienfeldt and Shnidman14] present nonhyperelliptic curves whose Ceresa cycles give rise to torsion classes in the Griffiths group, this problem remains open. The goal of this paper is to study hyperellipticity of tropical curves and graphs using cohomological invariants arising from the study of Ceresa triviality of algebraic curves defined over
![]() $\mathbb {C}(\!(t)\!)$
.
$\mathbb {C}(\!(t)\!)$
.
Degeneration techniques have long been used to study complex algebraic curves, both from the topological and algebraic/arithmetic perspectives. Tropical geometry provides a systematic framework for recording the combinatorial data of a stable degeneration as a tropical curve, that is, a graph with edge lengths and (possible) vertex weights. Topologically, stable degeneration is modeled by a family
![]() $\mathcal {C} \to D$
of Riemann surfaces over a small complex disc that is holomorphic over
$\mathcal {C} \to D$
of Riemann surfaces over a small complex disc that is holomorphic over
![]() $D\setminus x$
and the fiber over x is a stable curve. Restricting to an infinitesimal neighborhood of x, we obtain a smooth algebraic curve C over
$D\setminus x$
and the fiber over x is a stable curve. Restricting to an infinitesimal neighborhood of x, we obtain a smooth algebraic curve C over
![]() $\mathbb {C}(\!(t)\!)$
that has stable reduction. The tropical curve corresponding to this degeneration is the (vertex-weighted) dual graph of the special fiber and its edge lengths record the speeds to which the nodes in the special fiber are formed.
$\mathbb {C}(\!(t)\!)$
that has stable reduction. The tropical curve corresponding to this degeneration is the (vertex-weighted) dual graph of the special fiber and its edge lengths record the speeds to which the nodes in the special fiber are formed.
In [Reference Corey, Ellenberg and Li10], the authors define a Ceresa class in the topological and tropical contexts that agrees with the
![]() $\ell $
-adic Ceresa class—the image of the Ceresa cycle of a curve defined over
$\ell $
-adic Ceresa class—the image of the Ceresa cycle of a curve defined over
![]() $\mathbb {C}(\!(t)\!)$
under the
$\mathbb {C}(\!(t)\!)$
under the
![]() $\ell $
-adic Abel-Jacobi map—after applying a suitable comparison morphism. In this paper, we define the Ceresa–Zharkov class
$\ell $
-adic Abel-Jacobi map—after applying a suitable comparison morphism. In this paper, we define the Ceresa–Zharkov class
![]() $\mathbf {w}(\Gamma )$
of a tropical curve
$\mathbf {w}(\Gamma )$
of a tropical curve
![]() $\Gamma $
; this is a particular homomorphic image of the tropical Ceresa class, see §4 for the precise formulation. Notably, nontriviality of the Ceresa–Zharkov class implies nontriviality of the tropical Ceresa class.
$\Gamma $
; this is a particular homomorphic image of the tropical Ceresa class, see §4 for the precise formulation. Notably, nontriviality of the Ceresa–Zharkov class implies nontriviality of the tropical Ceresa class.
In an effort to emulate the notion of generic real edge lengths, we define a graph-theoretic Ceresa–Zharkov class
![]() $\mathbf {w}_{\tau }(G)$
(depending on a hyperelliptic quasi-involution
$\mathbf {w}_{\tau }(G)$
(depending on a hyperelliptic quasi-involution
![]() $\tau $
of the underlying genus-g surface
$\tau $
of the underlying genus-g surface
![]() $\Sigma _g$
, see §2.4), which lives in a module with coefficients in a polynomial ring whose variables correspond to the edges of G. Given a tropical curve
$\Sigma _g$
, see §2.4), which lives in a module with coefficients in a polynomial ring whose variables correspond to the edges of G. Given a tropical curve
![]() $\Gamma $
with underlying graph G, (a representative of) the class
$\Gamma $
with underlying graph G, (a representative of) the class
![]() $\mathbf {w}(\Gamma )$
is obtained by evaluating
$\mathbf {w}(\Gamma )$
is obtained by evaluating
![]() $\mathbf {w}_{\tau }(G)$
at the edge lengths of
$\mathbf {w}_{\tau }(G)$
at the edge lengths of
![]() $\Gamma $
. We define what it means for
$\Gamma $
. We define what it means for
![]() $\mathbf {w}_{\tau }(G)$
to be trivial—whence we call G Ceresa–Zharkov trivial—so that triviality of
$\mathbf {w}_{\tau }(G)$
to be trivial—whence we call G Ceresa–Zharkov trivial—so that triviality of
![]() $\mathbf {w}_{\tau }(G)$
implies triviality of
$\mathbf {w}_{\tau }(G)$
implies triviality of
![]() $\mathbf {w}(\Gamma )$
for any tropical curve with underlying graph G. However, nontriviality of
$\mathbf {w}(\Gamma )$
for any tropical curve with underlying graph G. However, nontriviality of
![]() $\mathbf {w}_{\tau }(G)$
does not imply nontriviality of
$\mathbf {w}_{\tau }(G)$
does not imply nontriviality of
![]() $\mathbf {w}(\Gamma )$
for a particular
$\mathbf {w}(\Gamma )$
for a particular
![]() $\Gamma $
with underlying graph G, rather we view this as saying that
$\Gamma $
with underlying graph G, rather we view this as saying that
![]() $\mathbf {w}(\Gamma )$
is generically nontrivial.
$\mathbf {w}(\Gamma )$
is generically nontrivial.
Our main theorem completely determines when a graph is Ceresa–Zharkov trivial, and it is closely related to hyperellipticity as we now explain. According to the tropical Torelli theorem, it is possible for nonisomorphic tropical curves to have isomorphic Jacobians as principally polarized tropical abelian varieties. A tropical curve whose Jacobian is isomorphic to that of a hyperelliptic tropical curve is said to be of hyperelliptic type. These tropical curves are defined in [Reference Corey9], where it is shown that being of hyperelliptic type depends only on the underling graph, is preserved when taking connected minors and its forbidden minors are
![]() $K_4$
and
$K_4$
and
![]() $L_3$
, see Figure 1.
$L_3$
, see Figure 1.
Theorem (Theorem 5.11).
A connected graph G of genus
![]() $g\geq 2$
is Ceresa–Zharkov trivial if and only if G is of hyperelliptic type, or equivalently, if and only if G has no
$g\geq 2$
is Ceresa–Zharkov trivial if and only if G is of hyperelliptic type, or equivalently, if and only if G has no
![]() $K_4$
or
$K_4$
or
![]() $L_3$
minor.
$L_3$
minor.

Figure 1 The graphs
![]() $K_4$
(left) and
$K_4$
(left) and
![]() $L_3$
(right).
$L_3$
(right).
Our choice for the name “Ceresa–Zharkov” class comes from a related construction due to Zharkov in [Reference Zharkov17]. Independent of the tropical Ceresa class described above, Zharkov uses the tropical analogs of curves, Jacobians, the Abel-Jacobi map and algebraic equivalence, to define and study a purely tropical Ceresa cycle. The main result of his paper is that this “tropical Ceresa cycle” is not (tropically) algebraically equivalent to 0 for a generic tropical curve with a
![]() $K_4$
subgraph. As observed in [Reference Corey, Ellenberg and Li10, Remark 7.3], when the underlying graph of a tropical curve is
$K_4$
subgraph. As observed in [Reference Corey, Ellenberg and Li10, Remark 7.3], when the underlying graph of a tropical curve is
![]() $K_4$
, Zharkov’s Ceresa cycle and notion of triviality coincides with our Ceresa–Zharkov class. This suggests the following question.
$K_4$
, Zharkov’s Ceresa cycle and notion of triviality coincides with our Ceresa–Zharkov class. This suggests the following question.
Question. What is the precise relationship between the Ceresa–Zharkov class and the tropical Ceresa cycle defined by Zharkov in [Reference Zharkov17]?
Here is an outline of the paper. In §2, we recall the construction of the topological and tropical Ceresa class from [Reference Corey, Ellenberg and Li10], then define the Ceresa–Zharkov class for tropical curves. Next, in §3, we define and study the polynomial algebra in which the graph-theoretic Ceresa–Zharkov class is defined. We define the Ceresa–Zharkov class for graphs in §4, as well as study its elementary properties. Finally, we investigate the relationship between Ceresa–Zharkov triviality and being of hyperelliptic type in §5, where we prove the main theorem.
2 Background
2.1 Stable graphs, tropical curves and tropical Jacobians
Given a graph G, denote by
![]() $V(G)$
and
$V(G)$
and
![]() $E(G)$
its set of vertices and edges, respectively. An edge of G is a loop if it is adjacent to a single vertex, and a pair of nonloop edges
$E(G)$
its set of vertices and edges, respectively. An edge of G is a loop if it is adjacent to a single vertex, and a pair of nonloop edges
![]() $(f,f')$
are parallel if they join the same pair of vertices. A (integral, unweighted) tropical curve
$(f,f')$
are parallel if they join the same pair of vertices. A (integral, unweighted) tropical curve
![]() $\Gamma $
consists of a finite connected graph G, possibly with loops and parallel edges, together with a positive integer-valued function
$\Gamma $
consists of a finite connected graph G, possibly with loops and parallel edges, together with a positive integer-valued function
![]() $c: E(G) \to \mathbb {Z}$
on the edge set
$c: E(G) \to \mathbb {Z}$
on the edge set
![]() $E(G)$
. We view G as the underlying graph of
$E(G)$
. We view G as the underlying graph of
![]() $\Gamma $
and
$\Gamma $
and
![]() $c(e)$
as the length of the edge e.Footnote
1
The genus of
$c(e)$
as the length of the edge e.Footnote
1
The genus of
![]() $\Gamma $
, written as
$\Gamma $
, written as
![]() $g(\Gamma )$
, is the first Betti number of G, that is,
$g(\Gamma )$
, is the first Betti number of G, that is,
A tropical curve
![]() $\Gamma $
is said to be 2-connected if G has no cut-vertices; in particular, such a graph cannot have a loop or a bridge.
$\Gamma $
is said to be 2-connected if G has no cut-vertices; in particular, such a graph cannot have a loop or a bridge.
Let
![]() $\Gamma = (G,c)$
be a genus
$\Gamma = (G,c)$
be a genus
![]() $g\geq 2$
tropical curve, and fix an orientation on G. The Jacobian of
$g\geq 2$
tropical curve, and fix an orientation on G. The Jacobian of
![]() $\Gamma $
is the real g-dimensional torus
$\Gamma $
is the real g-dimensional torus
together with the positive definite symmetric quadratic form
![]() $Q_{\Gamma }$
on
$Q_{\Gamma }$
on
![]() $H_1(G,\mathbb {R})$
given by
$H_1(G,\mathbb {R})$
given by
 $$ \begin{align*} Q_{\Gamma}\left( \sum_{e\in E(G)} a_{e} \cdot e , \sum_{e\in E(G)} b_{e} \cdot e \right) = \sum_{e\in E(G)} a_e b_e \cdot c(e). \end{align*} $$
$$ \begin{align*} Q_{\Gamma}\left( \sum_{e\in E(G)} a_{e} \cdot e , \sum_{e\in E(G)} b_{e} \cdot e \right) = \sum_{e\in E(G)} a_e b_e \cdot c(e). \end{align*} $$
The valence of a vertex v is the number of half edges adjacent to it; in particular a loop edge contributes 2 to the valence. A connected graph is stable if every vertex has valence at least
![]() $3$
, and a tropical curve is stable if its underlying graph is stable. Two tropical curves are tropically equivalent if one can be obtained from the other by a sequence of the following moves:
$3$
, and a tropical curve is stable if its underlying graph is stable. Two tropical curves are tropically equivalent if one can be obtained from the other by a sequence of the following moves:
-
- adding or removing a 1-valent vertex and its incident edge, or
-
- adding or removing a 2-valent vertex, preserving the underlying metric space.
Every tropical curve of genus
![]() $g\geq 2$
is tropically equivalent to a unique stable tropical curve.
$g\geq 2$
is tropically equivalent to a unique stable tropical curve.
A tropical curve is hyperelliptic if there is an involution
![]() $\sigma $
of
$\sigma $
of
![]() $\Gamma $
such that the quotient
$\Gamma $
such that the quotient
![]() $\Gamma /\sigma $
(in the sense of [Reference Chan8, § 2.2]) is a tree. A tropical curve is said to be of hyperelliptic type if its Jacobian is isomorphic to the Jacobian of a hyperelliptic tropical curve as a principally polarized tropical abelian variety. This notion is defined and studied in [Reference Corey9], where it is shown that
$\Gamma /\sigma $
(in the sense of [Reference Chan8, § 2.2]) is a tree. A tropical curve is said to be of hyperelliptic type if its Jacobian is isomorphic to the Jacobian of a hyperelliptic tropical curve as a principally polarized tropical abelian variety. This notion is defined and studied in [Reference Corey9], where it is shown that
![]() $\Gamma $
is of hyperelliptic type if and only if its underlying graph has no
$\Gamma $
is of hyperelliptic type if and only if its underlying graph has no
![]() $K_4$
or
$K_4$
or
![]() $L_3$
minor ([Reference Corey9, Theorem 1.1]); see Figure 1. Moreover, if
$L_3$
minor ([Reference Corey9, Theorem 1.1]); see Figure 1. Moreover, if
![]() $\Gamma $
is a 2-connected tropical curve of hyperelliptic type, then there is a hyperelliptic tropical curve
$\Gamma $
is a 2-connected tropical curve of hyperelliptic type, then there is a hyperelliptic tropical curve
![]() $\Gamma '$
such that the underlying graph of
$\Gamma '$
such that the underlying graph of
![]() $\Gamma $
is obtained from that of
$\Gamma $
is obtained from that of
![]() $\Gamma '$
by edge contractions.
$\Gamma '$
by edge contractions.
2.2 Dual graphs and multitwists from tropical curves
We assume familiarity with surface topology and refer the reader to [Reference Farb and Margalit12] for a comprehensive treatment. Given an orientable topological real surface S, possibly with boundary or punctures, denote by
![]() $\operatorname {\mathrm {Mod}}(S)$
its mapping class group. We write
$\operatorname {\mathrm {Mod}}(S)$
its mapping class group. We write
![]() $\Sigma _g$
for a closed genus-g surface and
$\Sigma _g$
for a closed genus-g surface and
![]() $\Sigma _g^1$
a genus g surface with one boundary component. We always identify
$\Sigma _g^1$
a genus g surface with one boundary component. We always identify
![]() $\Sigma _g^1$
as the subsurface of
$\Sigma _g^1$
as the subsurface of
![]() $\Sigma _g$
obtained by removing a small open disc. Given a curve
$\Sigma _g$
obtained by removing a small open disc. Given a curve
![]() $\gamma $
on
$\gamma $
on
![]() $\Sigma _g$
or
$\Sigma _g$
or
![]() $\Sigma _g^1$
, write
$\Sigma _g^1$
, write
![]() $T_{\gamma }$
for the (left-handed) Dehn twist about
$T_{\gamma }$
for the (left-handed) Dehn twist about
![]() $\gamma $
.
$\gamma $
.
Let
![]() $\Lambda $
be a finite collection of pairwise disjoint isotopy classes of simple closed curves on
$\Lambda $
be a finite collection of pairwise disjoint isotopy classes of simple closed curves on
![]() $\Sigma _g$
. Its (unweighted) dual graph is the graph with
$\Sigma _g$
. Its (unweighted) dual graph is the graph with
-
- a vertex
 $v_S$
for every connected component S of
$v_S$
for every connected component S of
 $\Sigma _g\setminus \bigcup _{\ell \in \Lambda } \ell $
, and
$\Sigma _g\setminus \bigcup _{\ell \in \Lambda } \ell $
, and -
- an edge
 $e_{\ell }$
between
$e_{\ell }$
between
 $v_S$
and
$v_S$
and
 $v_{S'}$
for each
$v_{S'}$
for each
 $\ell $
in the boundary of S and
$\ell $
in the boundary of S and
 $S'$
. The curve
$S'$
. The curve
 $\ell $
is said to be dual to
$\ell $
is said to be dual to
 $e_\ell $
.
$e_\ell $
.
Any connected genus-g graph is the dual graph of such a configuration. We are primarily interested in the case where
![]() $\Lambda $
is Lagrangian in the sense of [Reference Corey, Ellenberg and Li10], that is, each component S of
$\Lambda $
is Lagrangian in the sense of [Reference Corey, Ellenberg and Li10], that is, each component S of
![]() $\Sigma _g\setminus \bigcup _{\ell \in \Lambda } \ell $
has genus
$\Sigma _g\setminus \bigcup _{\ell \in \Lambda } \ell $
has genus
![]() $0$
.
$0$
.
Let
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
be two Lagrangian arrangements of curves on
$\Lambda _2$
be two Lagrangian arrangements of curves on
![]() $\Sigma _g$
as above such that their dual graphs,
$\Sigma _g$
as above such that their dual graphs,
![]() $G_1$
and
$G_1$
and
![]() $G_2$
, respectively, are stable. Then
$G_2$
, respectively, are stable. Then
![]() $G_1$
is isomorphic to
$G_1$
is isomorphic to
![]() $G_2$
if and only if there is a mapping class of
$G_2$
if and only if there is a mapping class of
![]() $\Sigma _g$
that takes
$\Sigma _g$
that takes
![]() $\Lambda _1$
to
$\Lambda _1$
to
![]() $\Lambda _2$
; this follows from the well-known identification of the quotient of the curve complex of
$\Lambda _2$
; this follows from the well-known identification of the quotient of the curve complex of
![]() $\Sigma _g$
by
$\Sigma _g$
by
![]() $\operatorname {\mathrm {Mod}}(\Sigma _g)$
with the tropical moduli space of genus g tropical curves of total edge length 1; see [Reference Chan, Galatius and Payne7, §1].
$\operatorname {\mathrm {Mod}}(\Sigma _g)$
with the tropical moduli space of genus g tropical curves of total edge length 1; see [Reference Chan, Galatius and Payne7, §1].
Given a genus-g tropical curve
![]() $\Gamma = (G,c)$
and
$\Gamma = (G,c)$
and
![]() $\Lambda $
an arrangement of curves on
$\Lambda $
an arrangement of curves on
![]() $\Sigma _g$
whose dual graph is G, define the multitwist
$\Sigma _g$
whose dual graph is G, define the multitwist
(Recall that we only consider tropical curves with integer edge lengths.) By the previous paragraph and the fact that
![]() $\sigma T_{\ell }\sigma ^{-1} = T_{\sigma (\ell )}$
for any
$\sigma T_{\ell }\sigma ^{-1} = T_{\sigma (\ell )}$
for any
![]() $\sigma \in \operatorname {\mathrm {Mod}}(\Sigma _g)$
, the mapping class
$\sigma \in \operatorname {\mathrm {Mod}}(\Sigma _g)$
, the mapping class
![]() $T_{\Gamma }$
is well defined up to conjugation in
$T_{\Gamma }$
is well defined up to conjugation in
![]() $\operatorname {\mathrm {Mod}}(\Sigma _g)$
. Furthermore,
$\operatorname {\mathrm {Mod}}(\Sigma _g)$
. Furthermore,
![]() $T_{\Gamma } = T_{\Gamma '}$
where
$T_{\Gamma } = T_{\Gamma '}$
where
![]() $\Gamma '$
is the unique stable tropical curve tropically equivalent to
$\Gamma '$
is the unique stable tropical curve tropically equivalent to
![]() $\Gamma $
.
$\Gamma $
.
2.3 The Johnson homomorphism
Let
![]() $\mathcal {I}_g^1 \leq \operatorname {\mathrm {Mod}}(\Sigma _g^1)$
, resp.
$\mathcal {I}_g^1 \leq \operatorname {\mathrm {Mod}}(\Sigma _g^1)$
, resp.
![]() $\mathcal {I}_g \leq \operatorname {\mathrm {Mod}}(\Sigma _g)$
, denote the Torelli group. Set
$\mathcal {I}_g \leq \operatorname {\mathrm {Mod}}(\Sigma _g)$
, denote the Torelli group. Set
The intersection product on H induces a
![]() $2$
-form
$2$
-form
![]() $\omega \in \wedge ^2H$
, and taking the exterior product with
$\omega \in \wedge ^2H$
, and taking the exterior product with
![]() $\omega $
yields an injection
$\omega $
yields an injection
![]() $H\hookrightarrow L$
. The Johnson homomorphism
$H\hookrightarrow L$
. The Johnson homomorphism
![]() $J:\mathcal {I}_g^1 \to L$
, resp.
$J:\mathcal {I}_g^1 \to L$
, resp.
![]() $J:\mathcal {I}_g \to L/H$
, may be characterized in the following way. By [Reference Powell16, Theorem 2], the Torelli group is generated by separating twists (Dehn twists about separating curves) and bounding pair maps (a product
$J:\mathcal {I}_g \to L/H$
, may be characterized in the following way. By [Reference Powell16, Theorem 2], the Torelli group is generated by separating twists (Dehn twists about separating curves) and bounding pair maps (a product
![]() $T_{\gamma }T_{\gamma '}^{-1}$
where
$T_{\gamma }T_{\gamma '}^{-1}$
where
![]() $\gamma ,\gamma '$
form a separating pair). If
$\gamma ,\gamma '$
form a separating pair). If
![]() $\gamma $
is a separating curve on
$\gamma $
is a separating curve on
![]() $\Sigma _g^{1}$
, then
$\Sigma _g^{1}$
, then
![]() $J(T_{\gamma }) = 0$
. Now, suppose that
$J(T_{\gamma }) = 0$
. Now, suppose that
![]() $\gamma ,\gamma '$
are a separating pair. The removal of
$\gamma ,\gamma '$
are a separating pair. The removal of
![]() $\gamma \cup \gamma '$
from
$\gamma \cup \gamma '$
from
![]() $\Sigma _g^1$
separates
$\Sigma _g^1$
separates
![]() $\Sigma _g^1$
into two surfaces S and
$\Sigma _g^1$
into two surfaces S and
![]() $S'$
; let S be the subsurface not containing the boundary component of
$S'$
; let S be the subsurface not containing the boundary component of
![]() $\Sigma _g^1$
. The form
$\Sigma _g^1$
. The form
![]() $\omega $
restricts to the intersection 2-form on S; denote this by
$\omega $
restricts to the intersection 2-form on S; denote this by
![]() $\omega _S$
. Then
$\omega _S$
. Then
where
![]() $[\gamma ]$
is oriented so that S appears on its right. The Johnson homomorphism on
$[\gamma ]$
is oriented so that S appears on its right. The Johnson homomorphism on
![]() $\mathcal {I}_g$
is defined in a similar way, except that one can choose either surface S or
$\mathcal {I}_g$
is defined in a similar way, except that one can choose either surface S or
![]() $S'$
in the above formula; the two possible expressions are equivalent modulo H.
$S'$
in the above formula; the two possible expressions are equivalent modulo H.
2.4 The tropical Ceresa class
Next, we briefly recall the definition of the Ceresa class of
![]() $\Gamma $
as was described in the Introduction; see [Reference Corey, Ellenberg and Li10] for more details. Fix a hyperelliptic quasi-involution
$\Gamma $
as was described in the Introduction; see [Reference Corey, Ellenberg and Li10] for more details. Fix a hyperelliptic quasi-involution
![]() $\tau $
, that is, a mapping class in
$\tau $
, that is, a mapping class in
![]() $\operatorname {\mathrm {Mod}}(\Sigma _g)$
that acts as
$\operatorname {\mathrm {Mod}}(\Sigma _g)$
that acts as
![]() $-I$
on H. Consider the map
$-I$
on H. Consider the map
where
![]() $[\gamma ,\tau ] = \gamma \tau \gamma ^{-1}\tau ^{-1}$
is the commutator. This is a 1-cocycle, and its class in
$[\gamma ,\tau ] = \gamma \tau \gamma ^{-1}\tau ^{-1}$
is the commutator. This is a 1-cocycle, and its class in
![]() $H^1(\operatorname {\mathrm {Mod}}(\Sigma _g),L/H)$
is independent of the choice of
$H^1(\operatorname {\mathrm {Mod}}(\Sigma _g),L/H)$
is independent of the choice of
![]() $\tau $
[Ibid., Proposition 2.1]. The
$\tau $
[Ibid., Proposition 2.1]. The
![]() $\tau $
-Ceresa cocycle of
$\tau $
-Ceresa cocycle of
![]() $\Gamma $
, denoted by
$\Gamma $
, denoted by
![]() $\nu _{\tau }(\Gamma )$
, is the restriction of
$\nu _{\tau }(\Gamma )$
, is the restriction of
![]() $\nu _{\tau }$
to
$\nu _{\tau }$
to
![]() $\langle T_{\Gamma }\rangle \cong \mathbb {Z}$
. Similarly, the Ceresa class of
$\langle T_{\Gamma }\rangle \cong \mathbb {Z}$
. Similarly, the Ceresa class of
![]() $\Gamma $
, denoted by
$\Gamma $
, denoted by
![]() $\nu (\Gamma )$
, is the class of
$\nu (\Gamma )$
, is the class of
![]() $\nu _{\tau }(\Gamma )$
in
$\nu _{\tau }(\Gamma )$
in
![]() $H^1(\mathbb {Z}, L/H)$
. Next, we will discuss several groups related to a filtration on L in which the Ceresa class lives and our computation will take place.
$H^1(\mathbb {Z}, L/H)$
. Next, we will discuss several groups related to a filtration on L in which the Ceresa class lives and our computation will take place.
A subgroup Y of H is Lagrangian if
![]() $Y_{\mathbb {Q}}$
is a maximal isotropic subspace of the symplectic vector space
$Y_{\mathbb {Q}}$
is a maximal isotropic subspace of the symplectic vector space
![]() $H_{\mathbb {Q}}$
(the symplectic form is induced by the intersection pairing on H) and
$H_{\mathbb {Q}}$
(the symplectic form is induced by the intersection pairing on H) and
![]() $H/Y$
is torsion-free. Let
$H/Y$
is torsion-free. Let
![]() $Y \leq H$
be the subgroup generated by the homology classes
$Y \leq H$
be the subgroup generated by the homology classes
![]() $\{[\ell ] \, : \, \ell \in \Lambda \}$
. This is a Lagrangian subgroup; see [Ibid., §6.1]. For values
$\{[\ell ] \, : \, \ell \in \Lambda \}$
. This is a Lagrangian subgroup; see [Ibid., §6.1]. For values
![]() $q=0,1,2,3$
, define the following filtrations on L and
$q=0,1,2,3$
, define the following filtrations on L and
![]() $L/H$
:
$L/H$
:
 $$ \begin{align*} F_q L = (\wedge^q Y) \wedge (\wedge^{3-q} H), \hspace{15pt} F_q (L/H) = \frac{F_{q}L + H}{H}, \hspace{15pt} \operatorname{\mathrm{gr}}_q^{F}(L/H) = \frac{F_q(L/H)}{F_{q-1}(L/H)}. \end{align*} $$
$$ \begin{align*} F_q L = (\wedge^q Y) \wedge (\wedge^{3-q} H), \hspace{15pt} F_q (L/H) = \frac{F_{q}L + H}{H}, \hspace{15pt} \operatorname{\mathrm{gr}}_q^{F}(L/H) = \frac{F_q(L/H)}{F_{q-1}(L/H)}. \end{align*} $$
These filtrations and groups associated with them are discussed in detail in [Ibid., §5].
Since
![]() $H\subset F_1L$
and
$H\subset F_1L$
and
![]() $F_3L \cap H = \{0\}$
, we have
$F_3L \cap H = \{0\}$
, we have
Denote by
![]() $\delta _{\Gamma }:H\to H$
the pushforward map on H induced by
$\delta _{\Gamma }:H\to H$
the pushforward map on H induced by
![]() $T_{\Gamma }$
. Recall from [Ibid., Lemma 5.1] that
$T_{\Gamma }$
. Recall from [Ibid., Lemma 5.1] that
![]() $\delta _\Gamma (F_qL)\subset F_{q+1}L $
and
$\delta _\Gamma (F_qL)\subset F_{q+1}L $
and
![]() $\delta _\Gamma $
preserves
$\delta _\Gamma $
preserves
![]() $\omega $
. Then the map
$\omega $
. Then the map
![]() $\delta _{\Gamma }-I$
restricts to the graded components
$\delta _{\Gamma }-I$
restricts to the graded components
Define groups
 $$ \begin{align*} A(\delta_{\Gamma}) &= \operatorname{\mathrm{im}}( H^1(\langle \delta_{\Gamma} \rangle, F_2(L/H)) \to H^1(\langle \delta_{\Gamma} \rangle, L/H)) \cong \frac{F_2L + H}{(\delta_{\Gamma}-I)(F_1L) + H} \\ B(\delta_{\Gamma}) &= \operatorname{\mathrm{coker}}(\delta_{\Gamma} - I: \operatorname{\mathrm{gr}}_1^{F}(L/H) \to \operatorname{\mathrm{gr}}_2^{F}(L/H)) \cong \frac{F_2L + H}{(\delta_{\Gamma}-I)(F_1L) + F_3L + H} \\ C(\delta_{\Gamma}) &= \operatorname{\mathrm{coker}}\left( (\delta_{\Gamma} - I)^2: \operatorname{\mathrm{gr}}_1^{F}(L/H) \to \operatorname{\mathrm{gr}}_3^{F}(L/H)\right) \cong \frac{F_3L}{(\delta_{\Gamma}-I)^2(F_1L)}. \end{align*} $$
$$ \begin{align*} A(\delta_{\Gamma}) &= \operatorname{\mathrm{im}}( H^1(\langle \delta_{\Gamma} \rangle, F_2(L/H)) \to H^1(\langle \delta_{\Gamma} \rangle, L/H)) \cong \frac{F_2L + H}{(\delta_{\Gamma}-I)(F_1L) + H} \\ B(\delta_{\Gamma}) &= \operatorname{\mathrm{coker}}(\delta_{\Gamma} - I: \operatorname{\mathrm{gr}}_1^{F}(L/H) \to \operatorname{\mathrm{gr}}_2^{F}(L/H)) \cong \frac{F_2L + H}{(\delta_{\Gamma}-I)(F_1L) + F_3L + H} \\ C(\delta_{\Gamma}) &= \operatorname{\mathrm{coker}}\left( (\delta_{\Gamma} - I)^2: \operatorname{\mathrm{gr}}_1^{F}(L/H) \to \operatorname{\mathrm{gr}}_3^{F}(L/H)\right) \cong \frac{F_3L}{(\delta_{\Gamma}-I)^2(F_1L)}. \end{align*} $$
The isomorphisms for
![]() $A(\delta _{\Gamma })$
and
$A(\delta _{\Gamma })$
and
![]() $B(\delta _{\Gamma })$
follow from [Ibid., Proposition 5.4]. These three groups are finite since
$B(\delta _{\Gamma })$
follow from [Ibid., Proposition 5.4]. These three groups are finite since
![]() $(\delta _{\Gamma }-I): \operatorname {\mathrm {gr}}_{q}^F(L/H) \to \operatorname {\mathrm {gr}}_{q+1}^F(L/H)$
is rationally surjective for
$(\delta _{\Gamma }-I): \operatorname {\mathrm {gr}}_{q}^F(L/H) \to \operatorname {\mathrm {gr}}_{q+1}^F(L/H)$
is rationally surjective for
![]() $q=1,2$
[Ibid.]. The identity map on
$q=1,2$
[Ibid.]. The identity map on
![]() $F_2L + H$
induces a homomorphism
$F_2L + H$
induces a homomorphism
![]() $A(\delta _{\Gamma }) \to B(\delta _{\Gamma })$
and we have an induced homomorphism
$A(\delta _{\Gamma }) \to B(\delta _{\Gamma })$
and we have an induced homomorphism
![]() $(\delta _{\Gamma } - I) : B(\delta _{\Gamma }) \to C(\delta _{\Gamma })$
. By [Ibid., Theorem 6.6], there is a hyperelliptic quasi-involution
$(\delta _{\Gamma } - I) : B(\delta _{\Gamma }) \to C(\delta _{\Gamma })$
. By [Ibid., Theorem 6.6], there is a hyperelliptic quasi-involution
![]() $\tau $
such that
$\tau $
such that
![]() $\nu _{\tau }(\Gamma )$
lies in
$\nu _{\tau }(\Gamma )$
lies in
![]() $F_2(L/H)$
. In practice, whenever we compute the tropical Ceresa class, we always use such a
$F_2(L/H)$
. In practice, whenever we compute the tropical Ceresa class, we always use such a
![]() $\tau $
. In particular, the Ceresa class
$\tau $
. In particular, the Ceresa class
![]() $\nu (\Gamma )$
lies in
$\nu (\Gamma )$
lies in
![]() $A(\delta _{\Gamma }) \subset H^1(\langle \delta _\Gamma \rangle ,L/H)$
. This implies the main result of [Ibid.], that
$A(\delta _{\Gamma }) \subset H^1(\langle \delta _\Gamma \rangle ,L/H)$
. This implies the main result of [Ibid.], that
![]() $\nu (\Gamma )$
is torsion. Now, we fix the following notation
$\nu (\Gamma )$
is torsion. Now, we fix the following notation
If
![]() $\tau $
satisfies
$\tau $
satisfies
![]() $\nu _\tau (\Gamma ) \in F_2(L/H)$
, by [Ibid., Proposition 6.7], the class
$\nu _\tau (\Gamma ) \in F_2(L/H)$
, by [Ibid., Proposition 6.7], the class
![]() $\mathbf {v}(\Gamma )$
has a particularly nice representative
$\mathbf {v}(\Gamma )$
has a particularly nice representative
The tropical curve
![]() $\Gamma $
is Ceresa trivial if
$\Gamma $
is Ceresa trivial if
![]() $\nu (\Gamma )=0$
. If
$\nu (\Gamma )=0$
. If
![]() $\Gamma $
is Ceresa trivial, then
$\Gamma $
is Ceresa trivial, then
![]() $\mathbf {v}(\Gamma ) = 0$
. Given the above formula,
$\mathbf {v}(\Gamma ) = 0$
. Given the above formula,
![]() $\mathbf {v}(\Gamma )$
is easier to compute than
$\mathbf {v}(\Gamma )$
is easier to compute than
![]() $\nu (\Gamma )$
, and therefore a good strategy to show that
$\nu (\Gamma )$
, and therefore a good strategy to show that
![]() $\Gamma $
is Ceresa nontrivial is to show that
$\Gamma $
is Ceresa nontrivial is to show that
![]() $\mathbf {v}(\Gamma ) \neq 0$
in
$\mathbf {v}(\Gamma ) \neq 0$
in
![]() $B(\delta _{\Gamma })$
.
$B(\delta _{\Gamma })$
.
3 The action of a multitwist on some polynomial algebras
3.1 Multitwist on the homology of a surface
Throughout, given
![]() $\mathbb {Z}$
-modules A and R, we set
$\mathbb {Z}$
-modules A and R, we set
![]() $A_R = A\otimes _{\mathbb {Z}} R$
. Let
$A_R = A\otimes _{\mathbb {Z}} R$
. Let
![]() $\Lambda $
be a collection of pairwise disjoint isotopy classes of simple closed curves on
$\Lambda $
be a collection of pairwise disjoint isotopy classes of simple closed curves on
![]() $\Sigma _{g}^{1}$
or
$\Sigma _{g}^{1}$
or
![]() $\Sigma _{g}$
. Define a polynomial ring
$\Sigma _{g}$
. Define a polynomial ring
which we denote by R when
![]() $\Lambda $
is clear from the context. Denote by
$\Lambda $
is clear from the context. Denote by
![]() $\langle a,b \rangle $
the intersection product of homology classes
$\langle a,b \rangle $
the intersection product of homology classes
![]() $a,b\in H = H_1(\Sigma _g,\mathbb {Z})$
. For any loop
$a,b\in H = H_1(\Sigma _g,\mathbb {Z})$
. For any loop
![]() $\ell \in \Lambda $
, let
$\ell \in \Lambda $
, let
![]() $\delta _{\ell }: H_{R} \to H_{R}$
be the homomorphism defined on simple tensors by
$\delta _{\ell }: H_{R} \to H_{R}$
be the homomorphism defined on simple tensors by
The map
![]() $\delta _{\ell }$
is an isomorphism with inverse
$\delta _{\ell }$
is an isomorphism with inverse
Because the loops in
![]() $\Lambda $
are pairwise disjoint, the
$\Lambda $
are pairwise disjoint, the
![]() $\delta _{\ell }$
’s pairwise commute. The homomorphism
$\delta _{\ell }$
’s pairwise commute. The homomorphism
![]() $\delta _\ell $
is related to the pushforward
$\delta _\ell $
is related to the pushforward
![]() $T_{\ell })_{*}:H\to H$
in the following way. Given a function
$T_{\ell })_{*}:H\to H$
in the following way. Given a function
![]() $c:\Lambda \to \mathbb {Z}$
, let
$c:\Lambda \to \mathbb {Z}$
, let
![]() $R\to \mathbb {Z}$
be the evaluation ring homomorphism
$R\to \mathbb {Z}$
be the evaluation ring homomorphism
![]() $x_{\ell }\mapsto c(\ell )$
. Then, under the identification
$x_{\ell }\mapsto c(\ell )$
. Then, under the identification
![]() $H \cong H\otimes _{\mathbb {Z}} R \otimes _{R} \mathbb {Z}$
, the map
$H \cong H\otimes _{\mathbb {Z}} R \otimes _{R} \mathbb {Z}$
, the map
![]() $\delta _{\ell } \otimes _{R} \operatorname {\mathrm {id}}_{\mathbb {Z}}$
is the pushforward of
$\delta _{\ell } \otimes _{R} \operatorname {\mathrm {id}}_{\mathbb {Z}}$
is the pushforward of
![]() $T_{\ell }^{c(\ell )}$
on H by [Reference Farb and Margalit12, Proposition 6.3].
$T_{\ell }^{c(\ell )}$
on H by [Reference Farb and Margalit12, Proposition 6.3].
Proposition 3.1. Given integers
![]() $\{a_{\ell } \, : \, \ell \in \Lambda \}$
, we have
$\{a_{\ell } \, : \, \ell \in \Lambda \}$
, we have
 $$ \begin{align*} \left(\prod_{\ell \in \Lambda} \delta_{\ell}^{a_{\ell}} \right) - I = \sum_{\ell\in \Lambda} a_{\ell} (\delta_{\ell}-I) \hspace{10pt} \text{ as maps } \hspace{10pt} H_R \to H_R. \end{align*} $$
$$ \begin{align*} \left(\prod_{\ell \in \Lambda} \delta_{\ell}^{a_{\ell}} \right) - I = \sum_{\ell\in \Lambda} a_{\ell} (\delta_{\ell}-I) \hspace{10pt} \text{ as maps } \hspace{10pt} H_R \to H_R. \end{align*} $$
Proof. It suffices to show
 $$ \begin{align*} &\delta_{\ell}\delta_{\ell'} - I = (\delta_{\ell} - I) + (\delta_{\ell'} - I), \text{ and } \\ &\delta_{\ell}^{-1} - I = -(\delta_{\ell}-I). \end{align*} $$
$$ \begin{align*} &\delta_{\ell}\delta_{\ell'} - I = (\delta_{\ell} - I) + (\delta_{\ell'} - I), \text{ and } \\ &\delta_{\ell}^{-1} - I = -(\delta_{\ell}-I). \end{align*} $$
The second formula follows readily from formulas (3.1) and (3.2). For the first formula, we have
 $$ \begin{align*} (\delta_{\ell}\delta_{\ell'}-I)(h\otimes a) &= \delta_{\ell}(h \otimes a + \langle h, [\ell'] \rangle [\ell'] \otimes x_{\ell'} a)-h\otimes a \\ &= (\delta_{\ell}-I)(h\otimes a) + \langle h, [\ell'] \rangle \delta_{\ell}( [\ell'] \otimes x_{\ell'} a) \\ &= (\delta_{\ell}-I)(h\otimes a) + \langle h, [\ell'] \rangle ([\ell'] \otimes x_{\ell'} a + \langle [\ell'], [\ell] \rangle [\ell] \otimes x_{\ell}x_{\ell'} a) \\ &= (\delta_{\ell}-I)(h\otimes a) + \langle h, [\ell'] \rangle[\ell']\otimes x_{\ell'} a \\ &=(\delta_{\ell} - I)(h\otimes a) + (\delta_{\ell'} - I)(h\otimes a).\\[-34pt] \end{align*} $$
$$ \begin{align*} (\delta_{\ell}\delta_{\ell'}-I)(h\otimes a) &= \delta_{\ell}(h \otimes a + \langle h, [\ell'] \rangle [\ell'] \otimes x_{\ell'} a)-h\otimes a \\ &= (\delta_{\ell}-I)(h\otimes a) + \langle h, [\ell'] \rangle \delta_{\ell}( [\ell'] \otimes x_{\ell'} a) \\ &= (\delta_{\ell}-I)(h\otimes a) + \langle h, [\ell'] \rangle ([\ell'] \otimes x_{\ell'} a + \langle [\ell'], [\ell] \rangle [\ell] \otimes x_{\ell}x_{\ell'} a) \\ &= (\delta_{\ell}-I)(h\otimes a) + \langle h, [\ell'] \rangle[\ell']\otimes x_{\ell'} a \\ &=(\delta_{\ell} - I)(h\otimes a) + (\delta_{\ell'} - I)(h\otimes a).\\[-34pt] \end{align*} $$
Next, define
![]() $\mathcal {B}=\langle \delta _{\ell } \, :\, \ell \in \Lambda \rangle $
, which is a free abelian subgroup of
$\mathcal {B}=\langle \delta _{\ell } \, :\, \ell \in \Lambda \rangle $
, which is a free abelian subgroup of
![]() $\operatorname {\mathrm {Aut}}(H_R)$
whose rank is equal to the number of nonseparating loops in
$\operatorname {\mathrm {Aut}}(H_R)$
whose rank is equal to the number of nonseparating loops in
![]() $\Lambda $
. Recall that
$\Lambda $
. Recall that
![]() $Y=\operatorname {\mathrm {span}}_{\mathbb {Z}}\{[\ell ] \, : \, \ell \in \Lambda \}$
, which is a Lagrangian subspace of H. The following is a straight-forward consequence of Equation (3.1) and Proposition 3.1.
$Y=\operatorname {\mathrm {span}}_{\mathbb {Z}}\{[\ell ] \, : \, \ell \in \Lambda \}$
, which is a Lagrangian subspace of H. The following is a straight-forward consequence of Equation (3.1) and Proposition 3.1.
Proposition 3.2. For any
![]() $f\in \mathcal {B}$
, we have
$f\in \mathcal {B}$
, we have
Denote by
![]() $\delta _{\Lambda }:H_R \to H_R$
the map
$\delta _{\Lambda }:H_R \to H_R$
the map
By Proposition 3.1, as a map
![]() $H_R\to H_R$
, we have
$H_R\to H_R$
, we have
3.2 The action of
 $\delta _{\Lambda }$
on
$\delta _{\Lambda }$
on
 $L_R$
$L_R$
The third exterior power of
![]() $\delta _{\Lambda }$
is a R-module homomorphism
$\delta _{\Lambda }$
is a R-module homomorphism
![]() $\wedge ^3(H_R) \to \wedge ^3(H_R)$
. However, the natural R-module homomorphism
$\wedge ^3(H_R) \to \wedge ^3(H_R)$
. However, the natural R-module homomorphism
is an isomorphism; thus we may view the third exterior power of
![]() $\delta _{\Lambda }$
as an R-module endomorphism of
$\delta _{\Lambda }$
as an R-module endomorphism of
![]() $L_R$
which we still denote by
$L_R$
which we still denote by
![]() $\delta _{\Lambda }$
. Next, we show that
$\delta _{\Lambda }$
. Next, we show that
![]() $\delta _{\Lambda }$
is an endomorphism of
$\delta _{\Lambda }$
is an endomorphism of
![]() $L_R/H_R$
, but we need the following more general setup.
$L_R/H_R$
, but we need the following more general setup.
Let
![]() $\iota : S\hookrightarrow \Sigma _g$
be a subsurface (possibly with boundary) of
$\iota : S\hookrightarrow \Sigma _g$
be a subsurface (possibly with boundary) of
![]() $\Sigma _g$
. The homology of S splits as
$\Sigma _g$
. The homology of S splits as
![]() $H_{1}(S,\mathbb {Z}) \cong V \oplus W$
, where V is the subgroup of H generated by the boundary curves of S and W is a symplectic subspace of H whose symplectic form, which we denote by
$H_{1}(S,\mathbb {Z}) \cong V \oplus W$
, where V is the subgroup of H generated by the boundary curves of S and W is a symplectic subspace of H whose symplectic form, which we denote by
![]() $\omega _S \in \wedge ^2W$
, is obtained by restricting the intersection of
$\omega _S \in \wedge ^2W$
, is obtained by restricting the intersection of
![]() $\Sigma _g$
to S. Let
$\Sigma _g$
to S. Let
![]() $\mathcal {B}_S$
be the subgroup of
$\mathcal {B}_S$
be the subgroup of
![]() $\mathcal {B}$
generated by the
$\mathcal {B}$
generated by the
![]() $\delta _{\ell }$
such that
$\delta _{\ell }$
such that
![]() $\ell $
is isotopic to a curve in S.
$\ell $
is isotopic to a curve in S.
Proposition 3.3. If
![]() $f\in \mathcal {B}_S$
, then
$f\in \mathcal {B}_S$
, then
-
1.
 $f(\omega _S) \equiv \omega _S \mod (V \wedge W)_R$
;
$f(\omega _S) \equiv \omega _S \mod (V \wedge W)_R$
; -
2.
 $(f-I)(h\wedge \omega _S) = (f-I)(h) \wedge \omega _S + f(h) \wedge \eta $
for some
$(f-I)(h\wedge \omega _S) = (f-I)(h) \wedge \omega _S + f(h) \wedge \eta $
for some
 $\ \eta \in (V\wedge W)_R$
.
$\ \eta \in (V\wedge W)_R$
.
Remark 3.4. As a consequence, if
![]() $S=\Sigma _g$
and
$S=\Sigma _g$
and
![]() $f\in \mathcal {B}$
, then
$f\in \mathcal {B}$
, then
![]() $(f-I)$
, as an endomorphism
$(f-I)$
, as an endomorphism
![]() $L_R\to L_R$
, takes
$L_R\to L_R$
, takes
![]() $H_R$
to
$H_R$
to
![]() $H_R$
(as an R-submodule of
$H_R$
(as an R-submodule of
![]() $L_R$
). In particular,
$L_R$
). In particular,
![]() $\delta _\Lambda -I$
may be regarded as an R-module endomorphism of
$\delta _\Lambda -I$
may be regarded as an R-module endomorphism of
![]() $L_R/H_R$
.
$L_R/H_R$
.
Proof of Proposition 3.3.
For (1), it suffices to show that
Choose a symplectic basis
![]() $\alpha _1,\ldots ,\alpha _g$
,
$\alpha _1,\ldots ,\alpha _g$
,
![]() $\beta _1,\ldots ,\beta _g$
of H such that
$\beta _1,\ldots ,\beta _g$
of H such that
![]() $\alpha _1,\ldots ,\alpha _h,\beta _1,\ldots ,\beta _h$
is a symplectic basis of W. This means that
$\alpha _1,\ldots ,\alpha _h,\beta _1,\ldots ,\beta _h$
is a symplectic basis of W. This means that
 $$ \begin{align*} \omega_S = \sum_{i=1}^{h} \alpha_i \wedge \beta_i. \end{align*} $$
$$ \begin{align*} \omega_S = \sum_{i=1}^{h} \alpha_i \wedge \beta_i. \end{align*} $$
Write
![]() $[\ell ] = \mu + \lambda $
, where
$[\ell ] = \mu + \lambda $
, where
![]() $\mu \in V$
and
$\mu \in V$
and
![]() $\lambda \in W$
. We have
$\lambda \in W$
. We have
 $$ \begin{align*} \lambda = \sum_{i=1}^h \left( - \langle \beta_i, [\ell] \rangle \alpha_i + \langle \alpha_i, [\ell] \rangle \beta_i \right). \end{align*} $$
$$ \begin{align*} \lambda = \sum_{i=1}^h \left( - \langle \beta_i, [\ell] \rangle \alpha_i + \langle \alpha_i, [\ell] \rangle \beta_i \right). \end{align*} $$
We compute
 $$ \begin{align*} \delta_{\ell}(\omega_S) &= \sum_{i=1}^{h} (\alpha_i + \langle \alpha_i, [\ell] \rangle [\ell] \otimes x_{\ell} ) \wedge (\beta_i + \langle \beta_i, [\ell] \rangle [\ell] \otimes x_{\ell} ) \\ &= \omega_S + \sum_{i=1}^{h}\left( \langle \beta_i, [\ell] \rangle \alpha_i\wedge [\ell] + \langle \alpha_i, [\ell] \rangle [\ell] \wedge \beta_i \right) \otimes x_{\ell} \\ &= \omega_S + [\ell] \wedge \sum_{i=1}^{h} \left( -\langle \beta_i, [\ell] \rangle \alpha_i + \langle \alpha_i, [\ell] \rangle \beta_i \right) \otimes x_{\ell} \\ & = \omega_S + \mu \wedge \lambda \otimes x_{\ell}, \end{align*} $$
$$ \begin{align*} \delta_{\ell}(\omega_S) &= \sum_{i=1}^{h} (\alpha_i + \langle \alpha_i, [\ell] \rangle [\ell] \otimes x_{\ell} ) \wedge (\beta_i + \langle \beta_i, [\ell] \rangle [\ell] \otimes x_{\ell} ) \\ &= \omega_S + \sum_{i=1}^{h}\left( \langle \beta_i, [\ell] \rangle \alpha_i\wedge [\ell] + \langle \alpha_i, [\ell] \rangle [\ell] \wedge \beta_i \right) \otimes x_{\ell} \\ &= \omega_S + [\ell] \wedge \sum_{i=1}^{h} \left( -\langle \beta_i, [\ell] \rangle \alpha_i + \langle \alpha_i, [\ell] \rangle \beta_i \right) \otimes x_{\ell} \\ & = \omega_S + \mu \wedge \lambda \otimes x_{\ell}, \end{align*} $$
from which formula (3.3) follows. For (2), we have
for some
![]() $\eta \in (V\wedge W)_R$
.
$\eta \in (V\wedge W)_R$
.
Similar to the integral setup in Section 2.4, we define a filtration on
![]() $ L_R$
and
$ L_R$
and
![]() $L_R/H_R$
:
$L_R/H_R$
:
and denote by
![]() $\operatorname {\mathrm {gr}}_{q}^{F}(L_R/H_R)$
the graded piece
$\operatorname {\mathrm {gr}}_{q}^{F}(L_R/H_R)$
the graded piece
 $$ \begin{align*} \operatorname{\mathrm{gr}}_{q}^{F}(L_R/H_R) := \frac{F_{q}(L_R/H_R)}{F_{q+1}(L_R/H_R)}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}_{q}^{F}(L_R/H_R) := \frac{F_{q}(L_R/H_R)}{F_{q+1}(L_R/H_R)}. \end{align*} $$
Proposition 3.5. Given
![]() $f\in \mathcal {B}$
and
$f\in \mathcal {B}$
and
![]() $h_1,h_2,h_3\in H$
, we have that
$h_1,h_2,h_3\in H$
, we have that
 $$ \begin{align*} (f-I)(h_1\wedge h_2 \wedge h_3) & \; = \; (f - I)h_1 \wedge h_2 \wedge h_3 + h_1 \wedge (f-I) h_2 \wedge h_3 + h_1 \wedge h_2 \wedge (f - I) h_3 \\ &\quad + (f - I)h_1 \wedge (f - I) h_2 \wedge h_3 + (f - I) h_1 \wedge h_2 \wedge (f - I) h_3\\ &\quad + h_1 \wedge (f - I) h_2 \wedge (f - I) h_3 \\ &\quad + (f - I)h_1 \wedge (f - I) h_2 \wedge (f - I) h_3. \end{align*} $$
$$ \begin{align*} (f-I)(h_1\wedge h_2 \wedge h_3) & \; = \; (f - I)h_1 \wedge h_2 \wedge h_3 + h_1 \wedge (f-I) h_2 \wedge h_3 + h_1 \wedge h_2 \wedge (f - I) h_3 \\ &\quad + (f - I)h_1 \wedge (f - I) h_2 \wedge h_3 + (f - I) h_1 \wedge h_2 \wedge (f - I) h_3\\ &\quad + h_1 \wedge (f - I) h_2 \wedge (f - I) h_3 \\ &\quad + (f - I)h_1 \wedge (f - I) h_2 \wedge (f - I) h_3. \end{align*} $$
In particular, we have that
![]() $(f-I)(F_{q}(L_R)) \subset F_{q+1}(L_R)$
.
$(f-I)(F_{q}(L_R)) \subset F_{q+1}(L_R)$
.
As a consequence of this proposition, the map
![]() $\delta _{\Lambda } -I$
on
$\delta _{\Lambda } -I$
on
![]() $L_R/H_R$
takes
$L_R/H_R$
takes
![]() $F_{q}(L_R/H_R)$
to
$F_{q}(L_R/H_R)$
to
![]() $F_{q+1}(L_R/H_R)$
and hence induces a map on graded components:
$F_{q+1}(L_R/H_R)$
and hence induces a map on graded components:
Proposition 3.6. As maps
![]() $\operatorname {\mathrm {gr}}_{q}^{F}(L_R/H_R) \to \operatorname {\mathrm {gr}}_{q+1}^{F}(L_R/H_R)$
, we have
$\operatorname {\mathrm {gr}}_{q}^{F}(L_R/H_R) \to \operatorname {\mathrm {gr}}_{q+1}^{F}(L_R/H_R)$
, we have
Proof. By Proposition 3.5, we have that
Now, apply Proposition 3.1.
In summary, the maps
![]() $\delta _{\Lambda }-I$
and
$\delta _{\Lambda }-I$
and
![]() $\sum _{\ell \in \Lambda }(\delta _{\ell }-I)$
coincide when viewed as maps on
$\sum _{\ell \in \Lambda }(\delta _{\ell }-I)$
coincide when viewed as maps on
![]() $H_R$
or the graded components
$H_R$
or the graded components
![]() $\operatorname {\mathrm {gr}}_{q}^F(L_R/H_R)$
but are different when viewed on the whole
$\operatorname {\mathrm {gr}}_{q}^F(L_R/H_R)$
but are different when viewed on the whole
![]() $L_R/H_R$
. This difference is important in the proof of Proposition 4.2.
$L_R/H_R$
. This difference is important in the proof of Proposition 4.2.
3.3 Configuration of loops from graphs
Let G be a connected genus-g stable graph and
![]() $\Lambda = \{\ell _e \, : \, e\in E(G)\}$
a collection of pairwise disjoint isotopy classes of simple closed curves on
$\Lambda = \{\ell _e \, : \, e\in E(G)\}$
a collection of pairwise disjoint isotopy classes of simple closed curves on
![]() $\Sigma _g$
whose dual graph is G, as in §2.2. The polynomial ring
$\Sigma _g$
whose dual graph is G, as in §2.2. The polynomial ring
is identified with
![]() $R[\Lambda ]$
by the relabeling
$R[\Lambda ]$
by the relabeling
![]() $x_{e} = x_{\ell _e}$
. We simply write R when the graph G is clear from context. Define the endomorphism
$x_{e} = x_{\ell _e}$
. We simply write R when the graph G is clear from context. Define the endomorphism
![]() $\delta _{G}$
on
$\delta _{G}$
on
![]() $H_{R}$
(respectively,
$H_{R}$
(respectively,
![]() $L_R$
and
$L_R$
and
![]() $L_{R}/H_{R}$
) by
$L_{R}/H_{R}$
) by
![]() $\delta _{G} = \delta _{\Lambda }$
. The map
$\delta _{G} = \delta _{\Lambda }$
. The map
![]() $\delta _G$
is closely related to the polarization of the Jacobian of a tropical curve, as we see in the following construction.
$\delta _G$
is closely related to the polarization of the Jacobian of a tropical curve, as we see in the following construction.
Define the symmetric quadratic form
![]() $Q_{G}$
on
$Q_{G}$
on
![]() $H_1(G,\mathbb {Z})\otimes R$
$H_1(G,\mathbb {Z})\otimes R$
 $$ \begin{align*} Q_{G}\left( \sum_{e\in E(G)} a_{e} \cdot e , \sum_{e\in E(G)} b_{e} \cdot e \right) = \sum_{e\in E(G)} a_e b_e \otimes x_{e}. \end{align*} $$
$$ \begin{align*} Q_{G}\left( \sum_{e\in E(G)} a_{e} \cdot e , \sum_{e\in E(G)} b_{e} \cdot e \right) = \sum_{e\in E(G)} a_e b_e \otimes x_{e}. \end{align*} $$
If
![]() $\Gamma = (G,c)$
is a tropical curve, then
$\Gamma = (G,c)$
is a tropical curve, then
![]() $Q_{\Gamma }$
is obtained from
$Q_{\Gamma }$
is obtained from
![]() $Q_{G}$
by the substitution
$Q_{G}$
by the substitution
![]() $x_e \mapsto c(e)$
. Let us give an explicit description of
$x_e \mapsto c(e)$
. Let us give an explicit description of
![]() $Q_{G}$
. Enumerate the edges of G by
$Q_{G}$
. Enumerate the edges of G by
![]() $e_1,\ldots ,e_n$
so that
$e_1,\ldots ,e_n$
so that
![]() $e_{g+1},\ldots ,e_{n}$
are the edges of a spanning tree T. Fix an arbitrary orientation on G. For
$e_{g+1},\ldots ,e_{n}$
are the edges of a spanning tree T. Fix an arbitrary orientation on G. For
![]() $j=1,\ldots , g$
, the graph
$j=1,\ldots , g$
, the graph
![]() $T\cup \{e_j\}$
contains a unique cycle
$T\cup \{e_j\}$
contains a unique cycle
![]() $\gamma _j$
; orient
$\gamma _j$
; orient
![]() $\gamma _j$
in the direction of
$\gamma _j$
in the direction of
![]() $e_j$
. The cycles
$e_j$
. The cycles
![]() $\gamma _1,\ldots ,\gamma _g$
form a basis of
$\gamma _1,\ldots ,\gamma _g$
form a basis of
![]() $H_1(G,\mathbb {Z})$
. Let
$H_1(G,\mathbb {Z})$
. Let
![]() $x_i = x_{e_i}$
. The
$x_i = x_{e_i}$
. The
![]() $(i,j)$
–entry of the matrix of
$(i,j)$
–entry of the matrix of
![]() $Q_{G}$
with respect to this basis is a linear form in the
$Q_{G}$
with respect to this basis is a linear form in the
![]() $x_k$
’s:
$x_k$
’s:
![]() $x_k$
appears with coefficient
$x_k$
appears with coefficient
![]() $1$
if
$1$
if
![]() $\gamma _i$
and
$\gamma _i$
and
![]() $\gamma _j$
traverse
$\gamma _j$
traverse
![]() $e_k$
in the same direction,
$e_k$
in the same direction,
![]() $-1$
if they traverse in the opposite direction and
$-1$
if they traverse in the opposite direction and
![]() $0$
if they do not meet at
$0$
if they do not meet at
![]() $e_k$
. For details and examples, see [Reference Bolognese, Brandt and Chua5, §4].
$e_k$
. For details and examples, see [Reference Bolognese, Brandt and Chua5, §4].
Now, we give the promised comparison to
![]() $\delta _{G}$
. Let
$\delta _{G}$
. Let
![]() $\ell _{k} = \ell _{e_k}$
. Orient
$\ell _{k} = \ell _{e_k}$
. Orient
![]() $\ell _k$
so that the subsurface corresponding to the target of
$\ell _k$
so that the subsurface corresponding to the target of
![]() $e_k$
lies to the left of
$e_k$
lies to the left of
![]() $\ell _k$
. Viewing G as a one-dimensional CW-complex, there is an embedding
$\ell _k$
. Viewing G as a one-dimensional CW-complex, there is an embedding
![]() $\iota : G\hookrightarrow \Sigma _g$
so that
$\iota : G\hookrightarrow \Sigma _g$
so that
![]() $\iota (e_j) \cap \ell _j$
is a point. For
$\iota (e_j) \cap \ell _j$
is a point. For
![]() $j=1,\ldots ,g$
, denote by
$j=1,\ldots ,g$
, denote by
![]() $\alpha _j$
and
$\alpha _j$
and
![]() $\beta _j$
the homology classes
$\beta _j$
the homology classes
![]() $-[\iota (\gamma _j)]$
and
$-[\iota (\gamma _j)]$
and
![]() $[\ell _j]$
, respectively; the orientations are chosen so that the signed intersection number of
$[\ell _j]$
, respectively; the orientations are chosen so that the signed intersection number of
![]() $\alpha _i$
with
$\alpha _i$
with
![]() $\beta _i$
is 1. Then
$\beta _i$
is 1. Then
![]() $\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$
is a symplectic basis for H.
$\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$
is a symplectic basis for H.
Since the
![]() $\ell \in \Lambda $
are pairwise nonintersecting, we have that
$\ell \in \Lambda $
are pairwise nonintersecting, we have that
![]() $\delta _{G}(\beta _j) = \beta _j$
. For the
$\delta _{G}(\beta _j) = \beta _j$
. For the
![]() $\alpha _j$
’s, we have
$\alpha _j$
’s, we have
 $$ \begin{align*} \delta_{G}(\alpha_j) = \alpha_{j} + \sum_{k=1}^{n} \langle \alpha_j, [\ell_{k}] \rangle [\ell_{k}] \otimes x_{k}. \end{align*} $$
$$ \begin{align*} \delta_{G}(\alpha_j) = \alpha_{j} + \sum_{k=1}^{n} \langle \alpha_j, [\ell_{k}] \rangle [\ell_{k}] \otimes x_{k}. \end{align*} $$
The
![]() $\beta _{i}$
–coefficient of
$\beta _{i}$
–coefficient of
![]() $\delta _{G}(\alpha _j)$
is
$\delta _{G}(\alpha _j)$
is
 $$ \begin{align*} \langle \alpha_i, \delta_{G}(\alpha_j) \rangle = \sum_{k=1}^{n} \langle \alpha_{i}, [\ell_k] \rangle \langle \alpha_j, [\ell_k] \rangle \otimes x_{k}. \end{align*} $$
$$ \begin{align*} \langle \alpha_i, \delta_{G}(\alpha_j) \rangle = \sum_{k=1}^{n} \langle \alpha_{i}, [\ell_k] \rangle \langle \alpha_j, [\ell_k] \rangle \otimes x_{k}. \end{align*} $$
This is a linear form in
![]() $x_{k}$
:
$x_{k}$
:
![]() $x_{k}$
appears with coefficient 1 if
$x_{k}$
appears with coefficient 1 if
![]() $\alpha _{i}$
and
$\alpha _{i}$
and
![]() $\alpha _{j}$
have the same intersection pairing with
$\alpha _{j}$
have the same intersection pairing with
![]() $\ell _{k}$
,
$\ell _{k}$
,
![]() $-1$
if they have opposite intersection pairing and 0 otherwise. Thus, the matrix of
$-1$
if they have opposite intersection pairing and 0 otherwise. Thus, the matrix of
![]() $\delta _G:H_R\to H_R$
with respect to the ordered basis
$\delta _G:H_R\to H_R$
with respect to the ordered basis
![]() $\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$
is given by
$\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$
is given by
 $$ \begin{align} \delta_{G} = \begin{pmatrix} I & 0 \\ Q_{G} & I \end{pmatrix}. \end{align} $$
$$ \begin{align} \delta_{G} = \begin{pmatrix} I & 0 \\ Q_{G} & I \end{pmatrix}. \end{align} $$
This allows us to view
![]() $Q_G$
as a map
$Q_G$
as a map
![]() $Y^{\perp }_{R} \to Y_R$
, where
$Y^{\perp }_{R} \to Y_R$
, where
Example 3.7. Consider
![]() $G=K_4$
, the complete graph on
$G=K_4$
, the complete graph on
![]() $4$
vertices, with the orientation as in Figure 2. To its right is an arrangement of curves on
$4$
vertices, with the orientation as in Figure 2. To its right is an arrangement of curves on
![]() $\Sigma _3$
whose dual graph is
$\Sigma _3$
whose dual graph is
![]() $K_4$
. Observe that each
$K_4$
. Observe that each
![]() $\ell _i$
is oriented so that the subsurface corresponding to the target of
$\ell _i$
is oriented so that the subsurface corresponding to the target of
![]() $e_i$
lies to the left of
$e_i$
lies to the left of
![]() $\ell _i$
. Also, observe that
$\ell _i$
. Also, observe that
![]() $\alpha _i$
is oriented so that the signed intersection product of
$\alpha _i$
is oriented so that the signed intersection product of
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i:=[\ell _i]$
is 1. The matrix
$\beta _i:=[\ell _i]$
is 1. The matrix
![]() $Q_G$
is
$Q_G$
is
 $$ \begin{align} Q_{G} = \begin{pmatrix} x_1 + x_5 + x_6 & -x_6 & -x_5 \\ -x_6 & x_2+x_4+x_6 & -x_4 \\ -x_5 & -x_4 & x_3+x_4+x_5 \end{pmatrix}. \end{align} $$
$$ \begin{align} Q_{G} = \begin{pmatrix} x_1 + x_5 + x_6 & -x_6 & -x_5 \\ -x_6 & x_2+x_4+x_6 & -x_4 \\ -x_5 & -x_4 & x_3+x_4+x_5 \end{pmatrix}. \end{align} $$

Figure 2 An arrangement of curves on
![]() $\Sigma _3$
with dual graph
$\Sigma _3$
with dual graph
![]() $K_4$
.
$K_4$
.
Combining the above connection between
![]() $\delta _{G}$
and
$\delta _{G}$
and
![]() $Q_{G}$
with Proposition 3.5, we deduce the following identities:
$Q_{G}$
with Proposition 3.5, we deduce the following identities:
 $$ \begin{align} (\delta_G-I)(\alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} ) &= Q_G(\alpha_i) \wedge \alpha_j \wedge \beta_k + \alpha_i \wedge Q_G(\alpha_j) \wedge \beta_k + Q_G(\alpha_i) \wedge Q_G(\alpha_j) \wedge \beta_k,\notag \\ (\delta_G-I)(\alpha_{i} \wedge \beta_{j} \wedge \beta_{k} ) &= Q_G(\alpha_i) \wedge \beta_j \wedge \beta_k, \\ (\delta_G-I)^2(\alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} ) &= 2\, Q_G(\alpha_i) \wedge Q_G(\alpha_j) \wedge \beta_k. \notag \end{align} $$
$$ \begin{align} (\delta_G-I)(\alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} ) &= Q_G(\alpha_i) \wedge \alpha_j \wedge \beta_k + \alpha_i \wedge Q_G(\alpha_j) \wedge \beta_k + Q_G(\alpha_i) \wedge Q_G(\alpha_j) \wedge \beta_k,\notag \\ (\delta_G-I)(\alpha_{i} \wedge \beta_{j} \wedge \beta_{k} ) &= Q_G(\alpha_i) \wedge \beta_j \wedge \beta_k, \\ (\delta_G-I)^2(\alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} ) &= 2\, Q_G(\alpha_i) \wedge Q_G(\alpha_j) \wedge \beta_k. \notag \end{align} $$
Remark 3.8. Denote by
![]() $R_d \subset R$
the subspace of homogeneous degree d-forms in R. Because the entries of
$R_d \subset R$
the subspace of homogeneous degree d-forms in R. Because the entries of
![]() $Q_{G}$
are linear forms in R, the map
$Q_{G}$
are linear forms in R, the map
![]() $\delta _G-I$
may be viewed as a map
$\delta _G-I$
may be viewed as a map
![]() $H_{R_d} \to H_{R_{d+1}}$
.
$H_{R_d} \to H_{R_{d+1}}$
.
4 The Ceresa–Zharkov class
4.1 Ceresa–Zharkov triviality
Recall that we view
![]() $\Sigma _g^1$
as a subsurface of
$\Sigma _g^1$
as a subsurface of
![]() $\Sigma _g$
obtained by removing a small open disc D from
$\Sigma _g$
obtained by removing a small open disc D from
![]() $\Sigma _g$
. Recall that a hyperelliptic quasi-involution is an element of
$\Sigma _g$
. Recall that a hyperelliptic quasi-involution is an element of
![]() $\operatorname {\mathrm {Mod}}(\Sigma _g^1)$
or
$\operatorname {\mathrm {Mod}}(\Sigma _g^1)$
or
![]() $\operatorname {\mathrm {Mod}}(\Sigma _g)$
whose action on
$\operatorname {\mathrm {Mod}}(\Sigma _g)$
whose action on
![]() $H = H_1(\Sigma _g^1,\mathbb {Z}) \cong H_{1}(\Sigma _g,\mathbb {Z})$
is
$H = H_1(\Sigma _g^1,\mathbb {Z}) \cong H_{1}(\Sigma _g,\mathbb {Z})$
is
![]() $-I$
. Let
$-I$
. Let
![]() $\tau '$
be a hyperelliptic quasi-involution on
$\tau '$
be a hyperelliptic quasi-involution on
![]() $\Sigma _g^{1}$
and
$\Sigma _g^{1}$
and
![]() $\tau $
its image under the natural map
$\tau $
its image under the natural map
![]() $\operatorname {\mathrm {Mod}}(\Sigma _g^1) \to \operatorname {\mathrm {Mod}}(\Sigma _g)$
. Let
$\operatorname {\mathrm {Mod}}(\Sigma _g^1) \to \operatorname {\mathrm {Mod}}(\Sigma _g)$
. Let
![]() $\Lambda '$
be a finite collection of pairwise disjoint isotopy classes of simple closed curves on
$\Lambda '$
be a finite collection of pairwise disjoint isotopy classes of simple closed curves on
![]() $\Sigma _g^1$
and
$\Sigma _g^1$
and
![]() $\Lambda $
the image of this collection under the inclusion
$\Lambda $
the image of this collection under the inclusion
![]() $\Sigma _g^1\hookrightarrow \Sigma _g$
; note that any finite collection of simple closed curves can be isotoped away from the disc D, so
$\Sigma _g^1\hookrightarrow \Sigma _g$
; note that any finite collection of simple closed curves can be isotoped away from the disc D, so
![]() $\Lambda $
may represent any finite collection of isotopy classes of simple closed curves on
$\Lambda $
may represent any finite collection of isotopy classes of simple closed curves on
![]() $\Sigma _g$
.
$\Sigma _g$
.
The
![]() $\tau '$
-Ceresa cocycle of
$\tau '$
-Ceresa cocycle of
![]() $\Lambda '$
, respectively the
$\Lambda '$
, respectively the
![]() $\tau $
-Ceresa cocycle of
$\tau $
-Ceresa cocycle of
![]() $\Lambda $
, is defined as
$\Lambda $
, is defined as
where J is the Johnson homomorphism; see §2.3. Define the
![]() $\tau $
-Ceresa–Zharkov cocycle as
$\tau $
-Ceresa–Zharkov cocycle as
When G is a genus-g graph, we write
![]() $\mathbf {v}_{\tau }(G) = \mathbf {v}_{\tau }(\Lambda )$
and
$\mathbf {v}_{\tau }(G) = \mathbf {v}_{\tau }(\Lambda )$
and
![]() $\mathbf {w}_{\tau }(G) = \mathbf {w}_{\tau }(\Lambda )$
, where
$\mathbf {w}_{\tau }(G) = \mathbf {w}_{\tau }(\Lambda )$
, where
![]() $\Lambda $
is an arrangement of curves whose dual graph is G. We say that G is Ceresa–Zharkov trivial if there is a
$\Lambda $
is an arrangement of curves whose dual graph is G. We say that G is Ceresa–Zharkov trivial if there is a
![]() $\tau $
such that
$\tau $
such that
![]() $\mathbf {w}_{\tau }(G) = 0$
. In Lemma 4.3, we show that this notion is a well-defined property of the graph G. While our primary interest is in
$\mathbf {w}_{\tau }(G) = 0$
. In Lemma 4.3, we show that this notion is a well-defined property of the graph G. While our primary interest is in
![]() $\mathbf {w}_{\tau }(G)$
, we occasionally need the class
$\mathbf {w}_{\tau }(G)$
, we occasionally need the class
![]() $\boldsymbol \mu _{\tau '}(\Lambda ')$
in §5. Compare these to the definitions of the Ceresa–Zharkov class and Ceresa–Zharkov triviality of a tropical curve defined in §2.4. In practice, when we compute the tropical Ceresa class for a tropical curve
$\boldsymbol \mu _{\tau '}(\Lambda ')$
in §5. Compare these to the definitions of the Ceresa–Zharkov class and Ceresa–Zharkov triviality of a tropical curve defined in §2.4. In practice, when we compute the tropical Ceresa class for a tropical curve
![]() $\Gamma $
, we use a hyperelliptic involution
$\Gamma $
, we use a hyperelliptic involution
![]() $\tau $
such that
$\tau $
such that
![]() $\nu _{\tau }(\Gamma )$
lies in
$\nu _{\tau }(\Gamma )$
lies in
![]() $F_2(L/H)$
as in §2.4. We do something similar in the graph-theoretic case. As before,
$F_2(L/H)$
as in §2.4. We do something similar in the graph-theoretic case. As before,
![]() $R_d\subset R$
denotes the linear subspace of degree d forms.
$R_d\subset R$
denotes the linear subspace of degree d forms.
Proposition 4.1. There exists a hyperelliptic quasi-involution
![]() $\tau '$
of
$\tau '$
of
![]() $\Sigma _g^1$
such that
$\Sigma _g^1$
such that
In particular,
![]() $\mathbf {v}_{\tau }(G)$
lies in
$\mathbf {v}_{\tau }(G)$
lies in
![]() $F_2(L/H) \otimes R_1$
and
$F_2(L/H) \otimes R_1$
and
![]() $\mathbf {w}_{\tau }(G)$
lies in
$\mathbf {w}_{\tau }(G)$
lies in
![]() $F_3L \otimes R_2$
, where
$F_3L \otimes R_2$
, where
![]() $\tau $
is the image of
$\tau $
is the image of
![]() $\tau '$
under
$\tau '$
under
![]() $\operatorname {\mathrm {Mod}}(\Sigma _g^1) \to \operatorname {\mathrm {Mod}}(\Sigma _g)$
.
$\operatorname {\mathrm {Mod}}(\Sigma _g^1) \to \operatorname {\mathrm {Mod}}(\Sigma _g)$
.
Proof. By [Reference Corey, Ellenberg and Li10, Theorem 6.6], there is a hyperelliptic quasi-involution
![]() $\tau '$
such that each
$\tau '$
such that each
![]() $J([T_{\ell },\tau '])$
lies in
$J([T_{\ell },\tau '])$
lies in
![]() $F_2L$
. The proposition now follows from Remark 3.8.
$F_2L$
. The proposition now follows from Remark 3.8.
Here is a characterization for Ceresa–Zharkov triviality when we use such a
![]() $\tau $
.
$\tau $
.
Proposition 4.2. If G is Ceresa–Zharkov trivial and
![]() $\mathbf {v}_{\tau }(G) \in F_2(L/H) \otimes R_1$
, then
$\mathbf {v}_{\tau }(G) \in F_2(L/H) \otimes R_1$
, then
Conversely, if there exists a
![]() $\tau $
such that Equation (4.1) holds, then G is Ceresa–Zharkov trivial.
$\tau $
such that Equation (4.1) holds, then G is Ceresa–Zharkov trivial.
To prove this proposition, we first derive a characterization of Ceresa–Zharkov triviality that works for any
![]() $\tau $
but is more cumbersome to state due to the fact that the endomorphism
$\tau $
but is more cumbersome to state due to the fact that the endomorphism
![]() $\delta _G-I$
of
$\delta _G-I$
of
![]() $L_R/H_R$
does not split as the sum
$L_R/H_R$
does not split as the sum
![]() $\sum _{e\in E(G)}(\delta _e-I)$
as discussed in §3.2.
$\sum _{e\in E(G)}(\delta _e-I)$
as discussed in §3.2.
Denote by
![]() $\psi _G:L_R/H_R \to L_R/H_R$
the composition
$\psi _G:L_R/H_R \to L_R/H_R$
the composition
 $$ \begin{align*} \psi_G = (\delta_G-I) \circ \left(\sum_{e\in E(G) }(\delta_e-1) \right). \end{align*} $$
$$ \begin{align*} \psi_G = (\delta_G-I) \circ \left(\sum_{e\in E(G) }(\delta_e-1) \right). \end{align*} $$
Lemma 4.3. The following are equivalent.
-
1. The graph G is Ceresa–Zharkov trivial;
-
2. for every hyperelliptic quasi-involution
 $\tau $
, we have
$\tau $
, we have
 $\mathbf {w}_{\tau }(G) \in \psi _G(L/H)$
;
$\mathbf {w}_{\tau }(G) \in \psi _G(L/H)$
; -
3. there is a hyperelliptic quasi-involution
 $\tau $
such that
$\tau $
such that
 $\mathbf {w}_{\tau }(G) \in \psi _G(L/H)$
.
$\mathbf {w}_{\tau }(G) \in \psi _G(L/H)$
.
Proof. Given hyperelliptic quasi-involutions
![]() $\tau , \tilde {\tau }$
, we have
$\tau , \tilde {\tau }$
, we have
and therefore
Suppose G is Ceresa–Zharkov trivial, say
![]() $\mathbf {w}_{\tau }(G)= 0$
for some
$\mathbf {w}_{\tau }(G)= 0$
for some
![]() $\tau $
. Applying
$\tau $
. Applying
![]() $\delta _G-I$
to formula (4.2), we see that (1)
$\delta _G-I$
to formula (4.2), we see that (1)
![]() $ \Rightarrow $
(2). The implication (2)
$ \Rightarrow $
(2). The implication (2)
![]() $\Rightarrow $
(3) is trivial. Now, suppose (3) is true, say
$\Rightarrow $
(3) is trivial. Now, suppose (3) is true, say
![]() $\mathbf {w}_{\tau }(G) = \psi _G(\mathbf {u})$
for some
$\mathbf {w}_{\tau }(G) = \psi _G(\mathbf {u})$
for some
![]() $\mathbf {u} \in L/H$
. By surjectivity of the Johnson homomorphism, there is a
$\mathbf {u} \in L/H$
. By surjectivity of the Johnson homomorphism, there is a
![]() $t\in \mathcal {I}_g$
such that
$t\in \mathcal {I}_g$
such that
![]() $J(t)=\mathbf {u}$
. The function
$J(t)=\mathbf {u}$
. The function
![]() $\tilde {\tau } = \tau t$
is a hyperelliptic quasi-involution, and by the above equation, we have
$\tilde {\tau } = \tau t$
is a hyperelliptic quasi-involution, and by the above equation, we have
Applying
![]() $\delta _G-I$
, we get
$\delta _G-I$
, we get
as required.
Proof of Proposition 4.2.
Let
![]() $\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$
be the symplectic basis of H from §3.3. We first record the image of the simple wedges under the map
$\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$
be the symplectic basis of H from §3.3. We first record the image of the simple wedges under the map
![]() $\psi _G$
using Proposition 3.5:
$\psi _G$
using Proposition 3.5:
 $$ \begin{align*} \psi_G(\alpha_{i} \wedge \alpha_{j} \wedge \alpha_{k} ) &= 2(Q_{G} \alpha_i \wedge Q_{G} \alpha_j \wedge \alpha_k + Q_{G} \alpha_i \wedge \alpha_j \wedge Q_{G} \alpha_k + \alpha_i \wedge Q_{G} \alpha_j \wedge Q_{G}\alpha_k) \\ &\quad +3 \, Q_G \alpha_i \wedge Q_{G} \alpha_j \wedge Q_{G} \alpha_k \\ \psi_G(\alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} ) &= 2\, Q_{G} \alpha_i \wedge Q_{G} \alpha_j \wedge \beta_k \\ \psi_G(\alpha_{i} \wedge \beta_{j} \wedge \beta_{k} ) &= \psi_G(\beta_{i} \wedge \beta_{j} \wedge \beta_{k} ) = 0. \end{align*} $$
$$ \begin{align*} \psi_G(\alpha_{i} \wedge \alpha_{j} \wedge \alpha_{k} ) &= 2(Q_{G} \alpha_i \wedge Q_{G} \alpha_j \wedge \alpha_k + Q_{G} \alpha_i \wedge \alpha_j \wedge Q_{G} \alpha_k + \alpha_i \wedge Q_{G} \alpha_j \wedge Q_{G}\alpha_k) \\ &\quad +3 \, Q_G \alpha_i \wedge Q_{G} \alpha_j \wedge Q_{G} \alpha_k \\ \psi_G(\alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} ) &= 2\, Q_{G} \alpha_i \wedge Q_{G} \alpha_j \wedge \beta_k \\ \psi_G(\alpha_{i} \wedge \beta_{j} \wedge \beta_{k} ) &= \psi_G(\beta_{i} \wedge \beta_{j} \wedge \beta_{k} ) = 0. \end{align*} $$
By this computation, formula (3.6) and the fact that
![]() $(\delta _G-I)^2|_{F_2(L/H)} = 0$
, we deduce that
$(\delta _G-I)^2|_{F_2(L/H)} = 0$
, we deduce that
![]() $ (\delta _{G}-I)^2|_{F_1(L/H)} = \psi _{G} |_{F_1(L/H)}$
. Therefore,
$ (\delta _{G}-I)^2|_{F_1(L/H)} = \psi _{G} |_{F_1(L/H)}$
. Therefore,
Suppose G is Ceresa–Zharkov trivial and that
![]() $\mathbf {v}_{\tau }(G) \in F_2(L/H) \otimes R_1$
. Then the class
$\mathbf {v}_{\tau }(G) \in F_2(L/H) \otimes R_1$
. Then the class
![]() $\mathbf {w}_{\tau }(G)$
lies in
$\mathbf {w}_{\tau }(G)$
lies in
![]() $\psi _G(L/H) \cap (F_3(L/H) \otimes R_2)$
by Lemma 4.3. So formula (4.1) follows from Equation (4.3), as required. Conversely, if there exists a
$\psi _G(L/H) \cap (F_3(L/H) \otimes R_2)$
by Lemma 4.3. So formula (4.1) follows from Equation (4.3), as required. Conversely, if there exists a
![]() $\tau $
such that formula (4.1) holds, then G is Ceresa–Zharkov trivial by Lemma 4.3 and formula (4.3).
$\tau $
such that formula (4.1) holds, then G is Ceresa–Zharkov trivial by Lemma 4.3 and formula (4.3).
4.2 Edge-contraction
In this section, we prove that Ceresa–Zharkov triviality is preserved under edge contraction. We prove in §5 that Ceresa–Zharkov triviality is a minor-closed property.
Suppose G is a connected graph,
![]() $f\in E(G)$
is a nonloop edge and
$f\in E(G)$
is a nonloop edge and
![]() $G/f$
the graph obtained from G by contracting f. Denote by
$G/f$
the graph obtained from G by contracting f. Denote by
![]() $\zeta _f:R[G] \to R[G/f]$
the map that evaluates
$\zeta _f:R[G] \to R[G/f]$
the map that evaluates
![]() $x_f$
to 0; this is a retract of the natural inclusion
$x_f$
to 0; this is a retract of the natural inclusion
![]() $R[G/f] \subset R[G]$
.
$R[G/f] \subset R[G]$
.
Proposition 4.4. With G and f as above, we have an equality of maps
![]() $(L/H)_{R[G]} \to (L/H)_{R[G/f]} $
:
$(L/H)_{R[G]} \to (L/H)_{R[G/f]} $
:
Also,
In particular, if G is Ceresa–Zharkov trivial, then so is
![]() $G/f$
.
$G/f$
.
Note that G and
![]() $G/f$
have the same genus g and both can be embedded into
$G/f$
have the same genus g and both can be embedded into
![]() $\Sigma _g$
as described in §3.3. So the same
$\Sigma _g$
as described in §3.3. So the same
![]() $\tau \in \operatorname {\mathrm {Mod}}(\Sigma _g)$
gives Ceresa cocycles of G and
$\tau \in \operatorname {\mathrm {Mod}}(\Sigma _g)$
gives Ceresa cocycles of G and
![]() $G/f$
.
$G/f$
.
Proof. First, consider the maps
![]() $1\otimes \zeta _f$
and
$1\otimes \zeta _f$
and
![]() $\delta _e-I$
on
$\delta _e-I$
on
![]() $H_R$
. We have
$H_R$
. We have
As a map
![]() $H_R \to H_R$
, by Proposition 3.1, we have
$H_R \to H_R$
, by Proposition 3.1, we have
 $$ \begin{align*} (1\otimes \zeta_f) (\delta_G-I) = (1\otimes \zeta_f) \sum_{e\in E(G)}(\delta_e-I) = \sum_{e\in E(G/f)} (\delta_e-I) (1\otimes \zeta_f) = (\delta_{G/f}-I)(1\otimes \zeta_f). \end{align*} $$
$$ \begin{align*} (1\otimes \zeta_f) (\delta_G-I) = (1\otimes \zeta_f) \sum_{e\in E(G)}(\delta_e-I) = \sum_{e\in E(G/f)} (\delta_e-I) (1\otimes \zeta_f) = (\delta_{G/f}-I)(1\otimes \zeta_f). \end{align*} $$
Thus, the identity in formula (4.4) holds as maps
![]() $H_{R[G]} \to H_{R[G/f]}$
, and one readily extends this as an identity of morphisms
$H_{R[G]} \to H_{R[G/f]}$
, and one readily extends this as an identity of morphisms
![]() $(L/H)_{R[G]} \to (L/H)_{R[G\setminus f]}$
using Proposition 3.5. Next, consider what happens for the Ceresa class. We have
$(L/H)_{R[G]} \to (L/H)_{R[G\setminus f]}$
using Proposition 3.5. Next, consider what happens for the Ceresa class. We have
 $$ \begin{align*} (1\otimes \zeta_f)(\mathbf{v}_{\tau}(G)) = (1\otimes \zeta_f) \sum_{e\in E(G)} J([T_{\ell_e}, \tau]) \otimes x_e = \sum_{e\in E(G/f)} J([T_{\ell_e}, \tau]) \otimes x_e = \mathbf{v}_{\tau}(G/f). \end{align*} $$
$$ \begin{align*} (1\otimes \zeta_f)(\mathbf{v}_{\tau}(G)) = (1\otimes \zeta_f) \sum_{e\in E(G)} J([T_{\ell_e}, \tau]) \otimes x_e = \sum_{e\in E(G/f)} J([T_{\ell_e}, \tau]) \otimes x_e = \mathbf{v}_{\tau}(G/f). \end{align*} $$
Finally, suppose G is Ceresa–Zharkov trivial, say
![]() $\mathbf {w}_{\tau }(G) = 0$
for some
$\mathbf {w}_{\tau }(G) = 0$
for some
![]() $\tau $
. Then,
$\tau $
. Then,
and therefore
![]() $G/f$
is Ceresa–Zharkov trivial.
$G/f$
is Ceresa–Zharkov trivial.
4.3 Tropical equivalence
Similar to the setting of tropical curves, two graphs are tropically equivalent if one can be obtained from the other via the following moves:
-
- adding or removing a 1-valent vertex together with its adjacent edge,
-
- subdividing a edge,
-
- contracting exactly one edge adjacent to a 2-valent vertex.
In this section, we show Ceresa–Zharkov triviality is preserved under all these moves and thus is a property of tropical equivalence classes. This fact is analogous to [Reference Corey, Ellenberg and Li10, Lemma 4.4] which asserts that tropically equivalent tropical curves have the same Ceresa class.
Lemma 4.5. Let G be a connected graph and e a separating edge. Then
-
1.
 $\delta _{G} = \delta _{G/e}$
;
$\delta _{G} = \delta _{G/e}$
; -
2.
 $\mathbf {v}_{\tau }(G) = \mathbf {v}_{\tau }(G/e)$
;
$\mathbf {v}_{\tau }(G) = \mathbf {v}_{\tau }(G/e)$
; -
3.
 $\mathbf {w}_{\tau }(G) = \mathbf {w}_{\tau }(G/e)$
.
$\mathbf {w}_{\tau }(G) = \mathbf {w}_{\tau }(G/e)$
.
In particular, the graph G is Ceresa–Zharkov trivial if and only if its 2-edge connectivization
![]() $G^2$
, which is obtained by contracting all separating edges of G, is Ceresa–Zharkov trivial.
$G^2$
, which is obtained by contracting all separating edges of G, is Ceresa–Zharkov trivial.
Proof. Statement (1) follows from the fact that
![]() $\delta _{e} = I$
whenever e is a separating edge. Statement (2) follows from the fact that
$\delta _{e} = I$
whenever e is a separating edge. Statement (2) follows from the fact that
![]() $[T_{\ell _e}, \tau ] = 1$
for any hyperelliptic quasi-involution
$[T_{\ell _e}, \tau ] = 1$
for any hyperelliptic quasi-involution
![]() $\tau $
. Finally, statement (3) is a consequence of (1) and (2).
$\tau $
. Finally, statement (3) is a consequence of (1) and (2).
Let G be a graph, and suppose
![]() $f \in E(G)$
is subdivided into two edges
$f \in E(G)$
is subdivided into two edges
![]() $e_1,e_2$
, producing the graph
$e_1,e_2$
, producing the graph
![]() $G'$
. Consider the ring map
$G'$
. Consider the ring map
![]() $\phi _f:R[G] \to R[G']$
given by
$\phi _f:R[G] \to R[G']$
given by
 $$ \begin{align*} \phi_f(x_e) = \left\{ \begin{array}{ll} x_e & \text{ if } e\neq f\\ x_{e_1} + x_{e_2} & \text{ if } e = f. \end{array} \right. \end{align*} $$
$$ \begin{align*} \phi_f(x_e) = \left\{ \begin{array}{ll} x_e & \text{ if } e\neq f\\ x_{e_1} + x_{e_2} & \text{ if } e = f. \end{array} \right. \end{align*} $$
Lemma 4.6. With the above notation, we have
as morphisms
![]() $(L/H)_{R[G]} \to (L/H)_{R[G']}$
, and
$(L/H)_{R[G]} \to (L/H)_{R[G']}$
, and
Proof. First, observe that the loops
![]() $\ell _{f}$
,
$\ell _{f}$
,
![]() $\ell _{e_1}$
and
$\ell _{e_1}$
and
![]() $\ell _{e_2}$
are isotopic to each other, thus
$\ell _{e_2}$
are isotopic to each other, thus
as elements of
![]() $\operatorname {\mathrm {Mod}}(\Sigma _g)$
, and as a consequence,
$\operatorname {\mathrm {Mod}}(\Sigma _g)$
, and as a consequence,
As morphisms
![]() $H_{R[G]} \to H_{R[G']}$
, we have
$H_{R[G]} \to H_{R[G']}$
, we have
 $$ \begin{align*} (1\otimes \phi_f) \circ (\delta_{e}-I) = \left\{ \begin{array}{ll} (\delta_{\ell_e}-I) \circ (1\otimes \phi_f) & \text{if } e \neq f \\ ((\delta_{\ell_{e_1}}-I) + (\delta_{\ell_{e_2}}-I) ) \circ (1\otimes \phi_f) & \text{if } e = f. \end{array} \right. \end{align*} $$
$$ \begin{align*} (1\otimes \phi_f) \circ (\delta_{e}-I) = \left\{ \begin{array}{ll} (\delta_{\ell_e}-I) \circ (1\otimes \phi_f) & \text{if } e \neq f \\ ((\delta_{\ell_{e_1}}-I) + (\delta_{\ell_{e_2}}-I) ) \circ (1\otimes \phi_f) & \text{if } e = f. \end{array} \right. \end{align*} $$
Therefore,
 $$ \begin{align*} (1\otimes \phi_f) \circ (\delta_{G}-I) &= (1\otimes \phi_f) \circ \sum_{e\in E(G)} (\delta_{\ell_{e}}-I) \\ &= \left((\delta_{\ell_{e_1}}-I) + (\delta_{\ell_{e_2}}-I) + \sum_{e\in E(G)\setminus f} (\delta_{\ell_{e}}-I) \right) \circ (1\otimes \phi_f) \\ &= (\delta_{G'}-I) \circ (1\otimes \phi_f). \end{align*} $$
$$ \begin{align*} (1\otimes \phi_f) \circ (\delta_{G}-I) &= (1\otimes \phi_f) \circ \sum_{e\in E(G)} (\delta_{\ell_{e}}-I) \\ &= \left((\delta_{\ell_{e_1}}-I) + (\delta_{\ell_{e_2}}-I) + \sum_{e\in E(G)\setminus f} (\delta_{\ell_{e}}-I) \right) \circ (1\otimes \phi_f) \\ &= (\delta_{G'}-I) \circ (1\otimes \phi_f). \end{align*} $$
Thus, the identity in Formula 4.5 holds as morphisms
![]() $H_{R[G]} \to H_{R[G']}$
. One readily extends this as an identity of morphisms
$H_{R[G]} \to H_{R[G']}$
. One readily extends this as an identity of morphisms
![]() $(L/H)_{R[G]} \to (L/H)_{R[G']}$
using Proposition 3.5.
$(L/H)_{R[G]} \to (L/H)_{R[G']}$
using Proposition 3.5.
For the statement regarding the Ceresa class, we compute
 $$ \begin{align*} (1\otimes \phi_f)(\mathbf{v}_{\tau}(G)) &= J([T_{\ell_f},\tau]) \otimes (x_{e_1} + x_{e_2}) + \sum_{e\in E(G) \setminus f} J([T_{\ell_e},\tau]) \otimes x_e \\ &= \sum_{e\in E(G')} J([T_{\ell_e},\tau]) \otimes x_e \\ &= \mathbf{v}_{\tau}(G').\\[-36pt] \end{align*} $$
$$ \begin{align*} (1\otimes \phi_f)(\mathbf{v}_{\tau}(G)) &= J([T_{\ell_f},\tau]) \otimes (x_{e_1} + x_{e_2}) + \sum_{e\in E(G) \setminus f} J([T_{\ell_e},\tau]) \otimes x_e \\ &= \sum_{e\in E(G')} J([T_{\ell_e},\tau]) \otimes x_e \\ &= \mathbf{v}_{\tau}(G').\\[-36pt] \end{align*} $$
Proposition 4.7. If G and
![]() $G'$
are tropically equivalent graphs, then G is Ceresa–Zharkov trivial if and only if
$G'$
are tropically equivalent graphs, then G is Ceresa–Zharkov trivial if and only if
![]() $G'$
is Ceresa–Zharkov trivial.
$G'$
is Ceresa–Zharkov trivial.
Proof. If
![]() $G'$
is obtained from G by adding or contracting an edge adjacent to a 1-valent vertex, then the claim follows from Lemma 4.5. Now, suppose
$G'$
is obtained from G by adding or contracting an edge adjacent to a 1-valent vertex, then the claim follows from Lemma 4.5. Now, suppose
![]() $G'$
is obtained from G by subdividing an edge
$G'$
is obtained from G by subdividing an edge
![]() $f \in E(G)$
into
$f \in E(G)$
into
![]() $e_1$
and
$e_1$
and
![]() $e_2$
. If
$e_2$
. If
![]() $G'$
is Ceresa–Zharkov trivial, then G is Ceresa–Zharkov trivial by Proposition 4.4. Conversely, if G is Ceresa–Zharkov trivial, say
$G'$
is Ceresa–Zharkov trivial, then G is Ceresa–Zharkov trivial by Proposition 4.4. Conversely, if G is Ceresa–Zharkov trivial, say
![]() $\mathbf {w}_{\tau }(G) = 0$
for some
$\mathbf {w}_{\tau }(G) = 0$
for some
![]() $\tau $
, then by Lemma 4.6 we have
$\tau $
, then by Lemma 4.6 we have
and hence
![]() $G'$
is Ceresa–Zharkov trivial.
$G'$
is Ceresa–Zharkov trivial.
4.4 Relation to the tropical Ceresa class
Let
![]() $\Gamma = (G,c)$
be a tropical curve. Recall from Section 2.4 that
$\Gamma = (G,c)$
be a tropical curve. Recall from Section 2.4 that
![]() $\mathbf {v}(\Gamma ) \in B(\delta _{\Gamma })$
is the image of the Ceresa class
$\mathbf {v}(\Gamma ) \in B(\delta _{\Gamma })$
is the image of the Ceresa class
![]() $\nu (\Gamma )$
under the map
$\nu (\Gamma )$
under the map
![]() $A(\delta ) \to B(\delta )$
. Given
$A(\delta ) \to B(\delta )$
. Given
![]() $c:E(G) \to \mathbb {Z}_{>0}$
, define homomorphisms
$c:E(G) \to \mathbb {Z}_{>0}$
, define homomorphisms
by the compositions
 $$ \begin{align*} &F_2(L/H)\otimes R_1 \to F_2(L/H) \to \operatorname{\mathrm{gr}}_2^F(L/H) \to B(\delta_{\Gamma}), \\ &F_3(L/H)\otimes R_2 \to F_3(L/H) \to \operatorname{\mathrm{gr}}_3^F(L/H) \to C(\delta_{\Gamma}), \end{align*} $$
$$ \begin{align*} &F_2(L/H)\otimes R_1 \to F_2(L/H) \to \operatorname{\mathrm{gr}}_2^F(L/H) \to B(\delta_{\Gamma}), \\ &F_3(L/H)\otimes R_2 \to F_3(L/H) \to \operatorname{\mathrm{gr}}_3^F(L/H) \to C(\delta_{\Gamma}), \end{align*} $$
respectively, where the first maps
![]() $ F_2(L/H)\otimes R_1 \to F_2(L/H)$
and
$ F_2(L/H)\otimes R_1 \to F_2(L/H)$
and
![]() $F_3(L/H)\otimes R_2 \to F_3(L/H)$
are given by the evaluation map
$F_3(L/H)\otimes R_2 \to F_3(L/H)$
are given by the evaluation map
![]() $h\otimes f \mapsto h\otimes f(c)$
. We say that
$h\otimes f \mapsto h\otimes f(c)$
. We say that
![]() $\Gamma $
is Ceresa–Zharkov trivial if
$\Gamma $
is Ceresa–Zharkov trivial if
![]() $\mathbf {w}(\Gamma ) = 0$
in
$\mathbf {w}(\Gamma ) = 0$
in
![]() $C(\delta _{\Gamma })$
.
$C(\delta _{\Gamma })$
.
Proposition 4.8. Let
![]() $\Gamma = (G,c)$
be a tropical curve, and let
$\Gamma = (G,c)$
be a tropical curve, and let
![]() $\tau $
be a hyperelliptic quasi-involution such that
$\tau $
be a hyperelliptic quasi-involution such that
![]() $\mathbf {v}_{\tau }(G)$
lies in
$\mathbf {v}_{\tau }(G)$
lies in
![]() $F_2(L/H)\otimes R_1$
. Then
$F_2(L/H)\otimes R_1$
. Then
In particular, if G is Ceresa–Zharkov trivial, then so is
![]() $\Gamma $
.
$\Gamma $
.
By [Reference Corey, Ellenberg and Li10, Proposition 4.6], if a tropical curve
![]() $\Gamma $
is hyperelliptic, then
$\Gamma $
is hyperelliptic, then
![]() $\Gamma $
is Ceresa trivial. Assuming Theorem 5.11, we derive a similar statement for tropical curves of hyperelliptic type and Ceresa–Zharkov triviality.
$\Gamma $
is Ceresa trivial. Assuming Theorem 5.11, we derive a similar statement for tropical curves of hyperelliptic type and Ceresa–Zharkov triviality.
Proposition 4.9. If a tropical curve
![]() $\Gamma $
is of hyperelliptic type, then
$\Gamma $
is of hyperelliptic type, then
![]() $\Gamma $
is Ceresa–Zharkov trivial.
$\Gamma $
is Ceresa–Zharkov trivial.
However, the converse to Proposition 4.9 is not true by Remark 5.8.
5 Ceresa–Zharkov trivial and tropical curves of hyperelliptic type
The main goal of this section is to prove Theorem 5.11, that a graph is Ceresa–Zharkov trivial if and only if it is of hyperelliptic type. Being of hyperelliptic type is a minor closed condition on graphs by [Reference Corey9, Proposition 3.8]. Because of this, Theorem 5.11 implies that Ceresa–Zharkov triviality is also a minor closed condition. Nevertheless, to prove this theorem, we need the fact that Ceresa–Zharkov triviality is preserved under edge contraction (Proposition 4.4) and under removal of a loop edge or an edge in a parallel pair (Proposition 5.1). The removal of these two types of edges are easier to handle for the following reason. Using Lemma 5.4, we may choose compatible homology bases and compatible hyperelliptic quasi-involutions of the Riemann surfaces corresponding to the original graph and the removal of such an edge. This allows for a direct comparison between the corresponding Ceresa–Zharkov classes.
Proposition 5.1. Consider either
-
1. a connected graph
 $G_1$
with a loop edge a, or
$G_1$
with a loop edge a, or -
2. a 2-connected graph
 $G_2$
with a pair of parallel edges
$G_2$
with a pair of parallel edges
 $(b,c)$
.
$(b,c)$
.
If
![]() $G_1$
, resp.
$G_1$
, resp.
![]() $G_2$
, is Ceresa–Zharkov trivial, then so is
$G_2$
, is Ceresa–Zharkov trivial, then so is
![]() $G_1\setminus a$
, resp.
$G_1\setminus a$
, resp.
![]() $G_2\setminus b$
.
$G_2\setminus b$
.
We begin by describing, for any connected graph G, the images
![]() $(\delta _{G}-I)(F_2(L_R/H_R))$
and
$(\delta _{G}-I)(F_2(L_R/H_R))$
and
![]() $(\delta _{G}-I)^2(F_1(L_R/H_R))$
. Order the edges of G by
$(\delta _{G}-I)^2(F_1(L_R/H_R))$
. Order the edges of G by
![]() $e_1,\ldots ,e_n$
so that
$e_1,\ldots ,e_n$
so that
![]() $e_{g+1},\ldots ,e_n$
are the edges of a spanning tree. Let
$e_{g+1},\ldots ,e_n$
are the edges of a spanning tree. Let
![]() $\alpha _1,\ldots ,\alpha _g,\beta _{1},\ldots ,\beta _{g}$
be the basis of
$\alpha _1,\ldots ,\alpha _g,\beta _{1},\ldots ,\beta _{g}$
be the basis of
![]() $H_1(\Sigma _g,\mathbb {Z})$
from §3.3, so
$H_1(\Sigma _g,\mathbb {Z})$
from §3.3, so
![]() $\delta _{G}$
has the form in Equation (3.4). Write
$\delta _{G}$
has the form in Equation (3.4). Write
![]() $q_{ij}$
for the entries of
$q_{ij}$
for the entries of
![]() $Q_G$
.
$Q_G$
.
Lemma 5.2. We have
 $$ \begin{align*} (\delta_G-I) \left( \sum_{i; j<k} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} \right)= \sum_{r<s<t} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}, \end{align*} $$
$$ \begin{align*} (\delta_G-I) \left( \sum_{i; j<k} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} \right)= \sum_{r<s<t} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}, \end{align*} $$
where
Proof. By formula (3.6), we have that
 $$ \begin{align*} (\delta_G-I) \sum_{i; j<k} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} = \sum_{i; j<k} Q_{G}(\alpha_i) \wedge \beta_j \wedge \beta_k \otimes b_{ijk} = \sum_{i; j<k; \ell} \beta_{\ell} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} q_{\ell i}. \end{align*} $$
$$ \begin{align*} (\delta_G-I) \sum_{i; j<k} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} = \sum_{i; j<k} Q_{G}(\alpha_i) \wedge \beta_j \wedge \beta_k \otimes b_{ijk} = \sum_{i; j<k; \ell} \beta_{\ell} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} q_{\ell i}. \end{align*} $$
Given
![]() $r<s<t$
one may extract the coefficient
$r<s<t$
one may extract the coefficient
![]() $c_{rst}$
for
$c_{rst}$
for
![]() $\beta _{r} \wedge \beta _{s} \wedge \beta _{t} $
.
$\beta _{r} \wedge \beta _{s} \wedge \beta _{t} $
.
Lemma 5.3. We have
 $$ \begin{align*} (\delta_G-I)^2 \sum_{i<j; k} \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} \otimes a_{ijk} = \sum_{r<s<t} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst} \hspace{10pt} \text{where} \hspace{5pt} c_{rst} = 2 \sum_{i<j} \, \begin{vmatrix} q_{ri} & q_{rj} & a_{ijr} \\ q_{si} & q_{sj} & a_{ijs} \\ q_{ti} & q_{tj} & a_{ijt} \end{vmatrix}. \end{align*} $$
$$ \begin{align*} (\delta_G-I)^2 \sum_{i<j; k} \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} \otimes a_{ijk} = \sum_{r<s<t} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst} \hspace{10pt} \text{where} \hspace{5pt} c_{rst} = 2 \sum_{i<j} \, \begin{vmatrix} q_{ri} & q_{rj} & a_{ijr} \\ q_{si} & q_{sj} & a_{ijs} \\ q_{ti} & q_{tj} & a_{ijt} \end{vmatrix}. \end{align*} $$
Proof. By Formula 3.6, we have that
 $$ \begin{align*} (\delta_G-I)^2 \left( \sum_{i<j; k} \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} \otimes a_{ijk} \right) &= \sum_{i<j; k} 2 Q_{G} \, \alpha_i \wedge Q_{G} \, \alpha_j \wedge \, \beta_k \otimes a_{ijk}\\ &= \sum_{i<j; k} \sum_{\ell<m} \beta_{\ell} \wedge \beta_{m} \wedge \beta_{k} \otimes 2a_{ijk} \begin{vmatrix} q_{\ell i} & q_{\ell j} \\ q_{m i} & q_{m j} \end{vmatrix}. \end{align*} $$
$$ \begin{align*} (\delta_G-I)^2 \left( \sum_{i<j; k} \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} \otimes a_{ijk} \right) &= \sum_{i<j; k} 2 Q_{G} \, \alpha_i \wedge Q_{G} \, \alpha_j \wedge \, \beta_k \otimes a_{ijk}\\ &= \sum_{i<j; k} \sum_{\ell<m} \beta_{\ell} \wedge \beta_{m} \wedge \beta_{k} \otimes 2a_{ijk} \begin{vmatrix} q_{\ell i} & q_{\ell j} \\ q_{m i} & q_{m j} \end{vmatrix}. \end{align*} $$
Given
![]() $r<s<t$
, the R-coefficient of
$r<s<t$
, the R-coefficient of
![]() $\beta _{r} \wedge \beta _{s} \wedge \beta _{t} $
is
$\beta _{r} \wedge \beta _{s} \wedge \beta _{t} $
is
 $$ \begin{align*} c_{rst} = 2\sum_{i<j} \left( a_{ijr} \begin{vmatrix} q_{si} & q_{sj} \\ q_{ti} & q_{tj} \end{vmatrix} - a_{ijs} \begin{vmatrix} q_{ri} & q_{rj} \\ q_{ti} & q_{tj} \end{vmatrix} + a_{ijt} \begin{vmatrix} q_{ri} & q_{rj} \\ q_{si} & q_{sj} \end{vmatrix} \right) \end{align*} $$
$$ \begin{align*} c_{rst} = 2\sum_{i<j} \left( a_{ijr} \begin{vmatrix} q_{si} & q_{sj} \\ q_{ti} & q_{tj} \end{vmatrix} - a_{ijs} \begin{vmatrix} q_{ri} & q_{rj} \\ q_{ti} & q_{tj} \end{vmatrix} + a_{ijt} \begin{vmatrix} q_{ri} & q_{rj} \\ q_{si} & q_{sj} \end{vmatrix} \right) \end{align*} $$
and the summand is exactly the
![]() $3\times 3$
determinant appearing in the lemma.
$3\times 3$
determinant appearing in the lemma.
Our next step is to show how the Ceresa classes of G and
![]() $G \setminus f$
are related. The two cases listed in Proposition 5.1 are similar, so we handle them in parallel. Let
$G \setminus f$
are related. The two cases listed in Proposition 5.1 are similar, so we handle them in parallel. Let
![]() $G_1$
be a connected graph with a loop edge a and let
$G_1$
be a connected graph with a loop edge a and let
![]() $G_2$
be a 2-connected graph with a pair of parallel edges
$G_2$
be a 2-connected graph with a pair of parallel edges
![]() $b,c$
. Let
$b,c$
. Let
![]() $\Lambda _1 = \{\ell _e \, : \, e\in E(G_1)\}$
and
$\Lambda _1 = \{\ell _e \, : \, e\in E(G_1)\}$
and
![]() $\Lambda _2 = \{\ell _e \, : \, e\in E(G_2)\}$
be two arrangements of isotopy classes of simple closed curves whose dual graphs are
$\Lambda _2 = \{\ell _e \, : \, e\in E(G_2)\}$
be two arrangements of isotopy classes of simple closed curves whose dual graphs are
![]() $G_1$
and
$G_1$
and
![]() $G_2$
, respectively. Suppose that
$G_2$
, respectively. Suppose that
![]() $\ell _{a}$
,
$\ell _{a}$
,
![]() $\ell _{b}$
,
$\ell _{b}$
,
![]() $\ell _{c}$
are as in Figure 3, and every other
$\ell _{c}$
are as in Figure 3, and every other
![]() $\ell _{e}$
lies in
$\ell _{e}$
lies in
![]() $\Sigma _{g}^1$
, the genus g subsurface with a boundary to the left of
$\Sigma _{g}^1$
, the genus g subsurface with a boundary to the left of
![]() $\gamma $
. To emphasize the dependence on the genus g, we write
$\gamma $
. To emphasize the dependence on the genus g, we write
where
![]() $n=0$
or
$n=0$
or
![]() $1$
. The inclusion
$1$
. The inclusion
![]() $\Sigma _{g}^1\hookrightarrow \Sigma _{g+1}$
induces an inclusion on homology groups which we use to identify
$\Sigma _{g}^1\hookrightarrow \Sigma _{g+1}$
induces an inclusion on homology groups which we use to identify
![]() $H(\Sigma _g) \cong H(\Sigma _g^1)$
as a subgroup of
$H(\Sigma _g) \cong H(\Sigma _g^1)$
as a subgroup of
![]() $H(\Sigma _{g+1})$
. Now, recall that we obtain
$H(\Sigma _{g+1})$
. Now, recall that we obtain
![]() $\Sigma _{g}$
from
$\Sigma _{g}$
from
![]() $\Sigma _{g}^1$
by attaching a disc along
$\Sigma _{g}^1$
by attaching a disc along
![]() $\gamma $
. Any two extensions of
$\gamma $
. Any two extensions of
![]() $\ell _{c}\cap \Sigma _{g}^1$
to
$\ell _{c}\cap \Sigma _{g}^1$
to
![]() $\Sigma _{g}$
are isotopic. Choose such an extension and denote it also by
$\Sigma _{g}$
are isotopic. Choose such an extension and denote it also by
![]() $\ell _{c}$
.
$\ell _{c}$
.

Figure 3 Arrangements of curves on
![]() $\Sigma _{g+1}$
with dual graphs
$\Sigma _{g+1}$
with dual graphs
![]() $G_1$
and
$G_1$
and
![]() $G_2$
where (left) a is a loop edge and (right)
$G_2$
where (left) a is a loop edge and (right)
![]() $(b,c)$
are parallel edges. Here, we identify
$(b,c)$
are parallel edges. Here, we identify
![]() $\Sigma _{g}^1$
with the subsurface of
$\Sigma _{g}^1$
with the subsurface of
![]() $\Sigma _{g+1}$
to the left of
$\Sigma _{g+1}$
to the left of
![]() $\gamma $
.
$\gamma $
.
We may view
![]() $\Lambda _1\setminus \{\ell _a\}$
as an arrangement of curves on
$\Lambda _1\setminus \{\ell _a\}$
as an arrangement of curves on
![]() $\Sigma _g$
or
$\Sigma _g$
or
![]() $\Sigma _g^1$
. We may also view
$\Sigma _g^1$
. We may also view
![]() $\Lambda _2\setminus \{\ell _b\}$
as an arrangement of curves on
$\Lambda _2\setminus \{\ell _b\}$
as an arrangement of curves on
![]() $\Sigma _g$
, and
$\Sigma _g$
, and
![]() $\Lambda _2\setminus \{\ell _b,\ell _{c}\}$
as an arrangement of curves on
$\Lambda _2\setminus \{\ell _b,\ell _{c}\}$
as an arrangement of curves on
![]() $\Sigma _g^1$
. Because
$\Sigma _g^1$
. Because
![]() $L(\Sigma _{g})/H(\Sigma _g)$
does not naturally embed into
$L(\Sigma _{g})/H(\Sigma _g)$
does not naturally embed into
![]() $L(\Sigma _{g+1})/H(\Sigma _{g+1})$
, we cannot directly compare
$L(\Sigma _{g+1})/H(\Sigma _{g+1})$
, we cannot directly compare
![]() $\mathbf {v}_{\tau }(\Lambda _1)$
with
$\mathbf {v}_{\tau }(\Lambda _1)$
with
![]() $\mathbf {v}_{\tau '}(\Lambda _1\setminus \{\ell _a\})$
, or
$\mathbf {v}_{\tau '}(\Lambda _1\setminus \{\ell _a\})$
, or
![]() $\mathbf {v}_{\tau }(\Lambda _2)$
with
$\mathbf {v}_{\tau }(\Lambda _2)$
with
![]() $\mathbf {v}_{\tau '}(\Lambda _2\setminus \{\ell _b\})$
. Instead, we compare these with Ceresa classes on
$\mathbf {v}_{\tau '}(\Lambda _2\setminus \{\ell _b\})$
. Instead, we compare these with Ceresa classes on
![]() $\Sigma _g^1$
in the following way.
$\Sigma _g^1$
in the following way.
Lemma 5.4. There are hyperelliptic quasi-involutions
![]() $\tau $
on
$\tau $
on
![]() $\Sigma _{g+1}$
,
$\Sigma _{g+1}$
,
![]() $\tau '$
on
$\tau '$
on
![]() $\Sigma _{g}$
and
$\Sigma _{g}$
and
![]() $\tau "$
on
$\tau "$
on
![]() $\Sigma _{g}^1$
, under the natural homomorphisms
$\Sigma _{g}^1$
, under the natural homomorphisms
 $$ \begin{align*} &L(\Sigma_g^1)_{R[\Lambda_1 \setminus \{\ell_a\}]} \to L(\Sigma_g)_{R[\Lambda_1 \setminus \{\ell_a\}]} / H(\Sigma_g)_{R[\Lambda_1 \setminus \{\ell_a\}]} \\ &L(\Sigma_g^1)_{R[\Lambda_1 \setminus \{\ell_a\}]} \hookrightarrow L(\Sigma_{g+1}^1)_{R[\Lambda_1]} \to L(\Sigma_{g+1})_{R[\Lambda_1]} / H(\Sigma_{g+1})_{R[\Lambda_1]} \end{align*} $$
$$ \begin{align*} &L(\Sigma_g^1)_{R[\Lambda_1 \setminus \{\ell_a\}]} \to L(\Sigma_g)_{R[\Lambda_1 \setminus \{\ell_a\}]} / H(\Sigma_g)_{R[\Lambda_1 \setminus \{\ell_a\}]} \\ &L(\Sigma_g^1)_{R[\Lambda_1 \setminus \{\ell_a\}]} \hookrightarrow L(\Sigma_{g+1}^1)_{R[\Lambda_1]} \to L(\Sigma_{g+1})_{R[\Lambda_1]} / H(\Sigma_{g+1})_{R[\Lambda_1]} \end{align*} $$
the class
![]() $\boldsymbol \mu _{\tau "}(\Lambda _1\setminus \{\ell _a\})$
maps to
$\boldsymbol \mu _{\tau "}(\Lambda _1\setminus \{\ell _a\})$
maps to
![]() $\mathbf {v}_{\tau '}(\Lambda _1\setminus \{\ell _a\})$
and
$\mathbf {v}_{\tau '}(\Lambda _1\setminus \{\ell _a\})$
and
![]() $\mathbf {v}_{\tau }(\Lambda _1)$
, respectively. Similarly, the natural homomorphisms
$\mathbf {v}_{\tau }(\Lambda _1)$
, respectively. Similarly, the natural homomorphisms
 $$ \begin{align*} L(\Sigma_g)_{R[\Lambda_2\setminus \{\ell_{b},\ell_{c}\}]} &\to L(\Sigma_g)_{R[\Lambda_2 \setminus \{\ell_b\}]}/H(\Sigma_g)_{R[\Lambda_2 \setminus \{\ell_{b}\}]} \\ L(\Sigma_g^1)_{R[\Lambda_2\setminus \{\ell_b,\ell_{c}\}]} &\hookrightarrow L(\Sigma_{g+1})_{R[\Lambda_2]} \to L(\Sigma_{g+1})_{R[\Lambda_2]}/H(\Sigma_{g+1})_{R[\Lambda_2]} \end{align*} $$
$$ \begin{align*} L(\Sigma_g)_{R[\Lambda_2\setminus \{\ell_{b},\ell_{c}\}]} &\to L(\Sigma_g)_{R[\Lambda_2 \setminus \{\ell_b\}]}/H(\Sigma_g)_{R[\Lambda_2 \setminus \{\ell_{b}\}]} \\ L(\Sigma_g^1)_{R[\Lambda_2\setminus \{\ell_b,\ell_{c}\}]} &\hookrightarrow L(\Sigma_{g+1})_{R[\Lambda_2]} \to L(\Sigma_{g+1})_{R[\Lambda_2]}/H(\Sigma_{g+1})_{R[\Lambda_2]} \end{align*} $$
take
![]() $\boldsymbol \mu _{\tau "}(\Lambda _2\setminus \{\ell _b,\ell _c\})$
to
$\boldsymbol \mu _{\tau "}(\Lambda _2\setminus \{\ell _b,\ell _c\})$
to
![]() $\mathbf {v}_{\tau '}(\Lambda _2\setminus \{\ell _b\})$
and
$\mathbf {v}_{\tau '}(\Lambda _2\setminus \{\ell _b\})$
and
![]() $\mathbf {v}_{\tau }(\Lambda _2)$
, respectively.
$\mathbf {v}_{\tau }(\Lambda _2)$
, respectively.
Furthermore, we may choose
![]() $\tau $
,
$\tau $
,
![]() $\tau '$
and
$\tau '$
and
![]() $\tau "$
so that all classes defined above live in the
$\tau "$
so that all classes defined above live in the
![]() $F_2$
part of the relevant filtration.
$F_2$
part of the relevant filtration.
Proof. Consider the surfaces homeomorphic to
![]() $\Sigma _{g+1}$
in Figure 3. These depict
$\Sigma _{g+1}$
in Figure 3. These depict
![]() $\Sigma _{g+1}$
embedded in
$\Sigma _{g+1}$
embedded in
![]() $\mathbb {R}^3$
and bounding a handlebody V, the ‘inside’ of the surface. Assume that the curves in
$\mathbb {R}^3$
and bounding a handlebody V, the ‘inside’ of the surface. Assume that the curves in
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
are meridians, that is, they bound properly embedded discs in V. We use these assumptions in the next paragraph to show that the Ceresa classes all belong to
$\Lambda _2$
are meridians, that is, they bound properly embedded discs in V. We use these assumptions in the next paragraph to show that the Ceresa classes all belong to
![]() $F_2$
.
$F_2$
.
Next, let
![]() $\tau $
be the hyperelliptic involution on
$\tau $
be the hyperelliptic involution on
![]() $\Sigma _{g+1}$
given by rotation by
$\Sigma _{g+1}$
given by rotation by
![]() $180^{\circ }$
about the axis illustrated in Figure 3; in particular,
$180^{\circ }$
about the axis illustrated in Figure 3; in particular,
![]() $\tau $
takes
$\tau $
takes
![]() $\ell _f$
to
$\ell _f$
to
![]() $\ell _f$
(reversing its orientation) for
$\ell _f$
(reversing its orientation) for
![]() $f=a$
, b, c. The map
$f=a$
, b, c. The map
![]() $\tau $
can be isotoped in a regular neighborhood of
$\tau $
can be isotoped in a regular neighborhood of
![]() $\gamma $
so that it fixes
$\gamma $
so that it fixes
![]() $\gamma $
pointwise. Consequently, the mapping class
$\gamma $
pointwise. Consequently, the mapping class
![]() $\tau \in \operatorname {\mathrm {Mod}}(\Sigma _{g+1})$
restricts to a hyperelliptic quasi-involution
$\tau \in \operatorname {\mathrm {Mod}}(\Sigma _{g+1})$
restricts to a hyperelliptic quasi-involution
![]() $\tau "$
on
$\tau "$
on
![]() $\Sigma _{g}^{1}$
; denote by
$\Sigma _{g}^{1}$
; denote by
![]() $\tau '$
the image of
$\tau '$
the image of
![]() $\tau "$
under the natural map
$\tau "$
under the natural map
![]() $\operatorname {\mathrm {Mod}}(\Sigma _{g}^1) \to \operatorname {\mathrm {Mod}}(\Sigma _{g})$
. Because all the curves in
$\operatorname {\mathrm {Mod}}(\Sigma _{g}^1) \to \operatorname {\mathrm {Mod}}(\Sigma _{g})$
. Because all the curves in
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
are meridians and the hyperelliptic quasi-involutions
$\Lambda _2$
are meridians and the hyperelliptic quasi-involutions
![]() $\tau $
,
$\tau $
,
![]() $\tau '$
and
$\tau '$
and
![]() $\tau "$
extend to homeomorphisms on the handlebodies, each
$\tau "$
extend to homeomorphisms on the handlebodies, each
![]() $J([T_{\ell }, \tau "])$
,
$J([T_{\ell }, \tau "])$
,
![]() $J([T_{\ell }, \tau '])$
and
$J([T_{\ell }, \tau '])$
and
![]() $J([T_{\ell }, \tau ])$
lie in
$J([T_{\ell }, \tau ])$
lie in
![]() $F_2$
by [Reference Corey, Ellenberg and Li10, Theorem 6.6], and therefore
$F_2$
by [Reference Corey, Ellenberg and Li10, Theorem 6.6], and therefore
![]() $\boldsymbol \mu _{\tau "}$
,
$\boldsymbol \mu _{\tau "}$
,
![]() $\mathbf {v}_{\tau '}$
and
$\mathbf {v}_{\tau '}$
and
![]() $\mathbf {v}_{\tau '}$
lie in
$\mathbf {v}_{\tau '}$
lie in
![]() $F_2\otimes R_1$
.
$F_2\otimes R_1$
.
Since
![]() $[T_{\ell _{f}},\tau ] = T_{\ell _{f}}T_{\tau (\ell _f)}^{-1}$
and
$[T_{\ell _{f}},\tau ] = T_{\ell _{f}}T_{\tau (\ell _f)}^{-1}$
and
![]() $\tau (\ell _f)$
is isotopic to
$\tau (\ell _f)$
is isotopic to
![]() $\ell _f$
for
$\ell _f$
for
![]() $f=a,b,c$
, we have that
$f=a,b,c$
, we have that
![]() $[T_{\ell _f},\tau ] = 1$
for
$[T_{\ell _f},\tau ] = 1$
for
![]() $f=a,b,c$
. Similarly, we have
$f=a,b,c$
. Similarly, we have
![]() $[T_{\ell _c},\tau '] = 1$
. Therefore,
$[T_{\ell _c},\tau '] = 1$
. Therefore,
The lemma follows from these computations.
Proof of Proposition 5.1.
Suppose that the graph G and edge
![]() $f\in E(G)$
are either
$f\in E(G)$
are either
-
1.
 $G=G_1$
and
$G=G_1$
and
 $f=a$
is a loop edge, or
$f=a$
is a loop edge, or -
2.
 $G=G_2$
, a 2-connected graph, and
$G=G_2$
, a 2-connected graph, and
 $f=b$
is parallel to another edge c.
$f=b$
is parallel to another edge c.
Let
![]() $g+1$
be the genus of G. Order the edges of G by
$g+1$
be the genus of G. Order the edges of G by
![]() $e_0, \ldots , e_g, e_{g+1}, \ldots , e_n$
such that the last
$e_0, \ldots , e_g, e_{g+1}, \ldots , e_n$
such that the last
![]() $n-(g+1)$
edges form a spanning tree of G and
$n-(g+1)$
edges form a spanning tree of G and
![]() $e_0 = f$
. In the second case, assume that
$e_0 = f$
. In the second case, assume that
![]() $e_1=c$
and orient
$e_1=c$
and orient
![]() $[\ell _{b}]$
and
$[\ell _{b}]$
and
![]() $[\ell _{c}]$
in the same direction. This is possible since
$[\ell _{c}]$
in the same direction. This is possible since
![]() $G_2$
is 2-connected, so
$G_2$
is 2-connected, so
![]() $b,c$
are not a separating pair. Denote by
$b,c$
are not a separating pair. Denote by
![]() $\alpha _{0},\ldots ,\alpha _g,\beta _0,\ldots ,\beta _g$
the basis described in Section 3.3. This identifies
$\alpha _{0},\ldots ,\alpha _g,\beta _0,\ldots ,\beta _g$
the basis described in Section 3.3. This identifies
![]() $Q_{G\setminus f}$
with the lower-right
$Q_{G\setminus f}$
with the lower-right
![]() $g\times g$
submatrix of
$g\times g$
submatrix of
![]() $Q_{G}$
. Let
$Q_{G}$
. Let
![]() $q_{ij}$
denote the coordinates of
$q_{ij}$
denote the coordinates of
![]() $Q_{G}$
. When
$Q_{G}$
. When
![]() $G=G_1$
, we have
$G=G_1$
, we have
and when
![]() $G=G_2$
, we have
$G=G_2$
, we have
By Lemma 5.4, there are hyperelliptic quasi-involutions
![]() $\tau $
on
$\tau $
on
![]() $\Sigma _{g+1}$
and
$\Sigma _{g+1}$
and
![]() $\tau '$
on
$\tau '$
on
![]() $\Sigma _{g}$
such that
$\Sigma _{g}$
such that
 $$ \begin{align*} \mathbf{v}_{\tau}(G) = \sum_{ \substack{1\leq i\leq g \\ 1\leq j<k\leq g}} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} \hspace{10pt} \text{ in } \hspace{10pt} L(\Sigma_{g+1})_{R[G]}/H(\Sigma_{g+1})_{R[G]} \\ \mathbf{v}_{\tau'}(G\setminus f) = \sum_{\substack{1\leq i\leq g\\ 1\leq j<k\leq g}} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} \hspace{10pt} \text{ in } \hspace{10pt} L(\Sigma_{g})_{R[G\setminus f]}/H(\Sigma_{g})_{R[G\setminus f]}, \end{align*} $$
$$ \begin{align*} \mathbf{v}_{\tau}(G) = \sum_{ \substack{1\leq i\leq g \\ 1\leq j<k\leq g}} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} \hspace{10pt} \text{ in } \hspace{10pt} L(\Sigma_{g+1})_{R[G]}/H(\Sigma_{g+1})_{R[G]} \\ \mathbf{v}_{\tau'}(G\setminus f) = \sum_{\substack{1\leq i\leq g\\ 1\leq j<k\leq g}} \alpha_{i} \wedge \beta_{j} \wedge \beta_{k} \otimes b_{ijk} \hspace{10pt} \text{ in } \hspace{10pt} L(\Sigma_{g})_{R[G\setminus f]}/H(\Sigma_{g})_{R[G\setminus f]}, \end{align*} $$
where
![]() $b_{ijk}$
’s are linear forms in
$b_{ijk}$
’s are linear forms in
![]() $R[G\setminus f]\subset R[G]$
. Implicit in this description is that
$R[G\setminus f]\subset R[G]$
. Implicit in this description is that
![]() $b_{0jk} = 0$
and
$b_{0jk} = 0$
and
![]() $b_{i0k}=0$
. Because G is Ceresa–Zharkov trivial, by Proposition 4.2, there is a
$b_{i0k}=0$
. Because G is Ceresa–Zharkov trivial, by Proposition 4.2, there is a
![]() $\mathbf {u}\in F_1(L/H)$
, say
$\mathbf {u}\in F_1(L/H)$
, say
 $$ \begin{align*} \mathbf{u}= \sum_{\substack{0\leq i<j \leq g \\ 0\leq k \leq g}} a_{ijk} \cdot \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} \end{align*} $$
$$ \begin{align*} \mathbf{u}= \sum_{\substack{0\leq i<j \leq g \\ 0\leq k \leq g}} a_{ijk} \cdot \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k} \end{align*} $$
with
![]() $a_{ijk} \in \mathbb {Z}$
such that
$a_{ijk} \in \mathbb {Z}$
such that
![]() $\mathbf {w}_{\tau }(G) = (\delta _G-I)^2(\mathbf {u})$
. We will show that
$\mathbf {w}_{\tau }(G) = (\delta _G-I)^2(\mathbf {u})$
. We will show that
![]() $\mathbf {w}_{\tau '}(G\setminus f)$
lies in the image
$\mathbf {w}_{\tau '}(G\setminus f)$
lies in the image
![]() $(\delta _{G\setminus f}-I)^2(F_1(L(\Sigma _g)/H(\Sigma _g)))$
, whence
$(\delta _{G\setminus f}-I)^2(F_1(L(\Sigma _g)/H(\Sigma _g)))$
, whence
![]() $G\setminus f$
is Ceresa–Zharkov trivial by Proposition 4.2. Because
$G\setminus f$
is Ceresa–Zharkov trivial by Proposition 4.2. Because
![]() $b_{0jk} = 0$
, we have
$b_{0jk} = 0$
, we have
 $$ \begin{align} c_{rst} := \sum_{i=0}^{g} (b_{irs}q_{ti} - b_{irt}q_{si} + b_{ist}q_{ri}) = \sum_{i=1}^{g} (b_{irs}q_{ti} - b_{irt}q_{si} + b_{ist}q_{ri}) \end{align} $$
$$ \begin{align} c_{rst} := \sum_{i=0}^{g} (b_{irs}q_{ti} - b_{irt}q_{si} + b_{ist}q_{ri}) = \sum_{i=1}^{g} (b_{irs}q_{ti} - b_{irt}q_{si} + b_{ist}q_{ri}) \end{align} $$
for
![]() $0\leq r<s<t \leq g$
. Therefore, by Lemma 5.2, we have
$0\leq r<s<t \leq g$
. Therefore, by Lemma 5.2, we have
 $$ \begin{align*} \mathbf{w}_{\tau}(G) &= (\delta_G-I)(\mathbf{v}_{\tau}(G)) = \sum_{0\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst} \hspace{15pt} \text{and} \\ \mathbf{w}_{\tau'}(G\setminus f) &= (\delta_{G\setminus f}-I)(\mathbf{v}_{\tau'}(G\setminus f)) = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}. \end{align*} $$
$$ \begin{align*} \mathbf{w}_{\tau}(G) &= (\delta_G-I)(\mathbf{v}_{\tau}(G)) = \sum_{0\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst} \hspace{15pt} \text{and} \\ \mathbf{w}_{\tau'}(G\setminus f) &= (\delta_{G\setminus f}-I)(\mathbf{v}_{\tau'}(G\setminus f)) = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}. \end{align*} $$
By the equality
![]() $\mathbf {w}_{\tau }(G) = (\delta _{G}-I)^2(\mathbf {u})$
and Lemma 5.3, we have
$\mathbf {w}_{\tau }(G) = (\delta _{G}-I)^2(\mathbf {u})$
and Lemma 5.3, we have
 $$ \begin{align} c_{rst} = 2\sum_{0\leq i<j \leq g} \begin{vmatrix} q_{ri} & q_{rj} & a_{ijr} \\ q_{si} & q_{sj} & a_{ijs} \\ q_{ti} & q_{tj} & a_{ijt} \end{vmatrix}. \end{align} $$
$$ \begin{align} c_{rst} = 2\sum_{0\leq i<j \leq g} \begin{vmatrix} q_{ri} & q_{rj} & a_{ijr} \\ q_{si} & q_{sj} & a_{ijs} \\ q_{ti} & q_{tj} & a_{ijt} \end{vmatrix}. \end{align} $$
Set
 $$ \begin{align*} \mathbf{u}'= \sum_{\substack{1\leq i<j \leq g \\ 1\leq k \leq g}} a_{ijk} \cdot \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k}. \end{align*} $$
$$ \begin{align*} \mathbf{u}'= \sum_{\substack{1\leq i<j \leq g \\ 1\leq k \leq g}} a_{ijk} \cdot \alpha_{i} \wedge \alpha_{j} \wedge \beta_{k}. \end{align*} $$
Then
 $$ \begin{align*} (\delta_{G\setminus f}-I)^2(\mathbf{u}') = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}' \hspace{15pt} \text{where} \hspace{15pt} c_{rst}' = 2\sum_{1\leq i<j \leq g} \begin{vmatrix} q_{ri} & q_{rj} & a_{ijr} \\ q_{si} & q_{sj} & a_{ijs} \\ q_{ti} & q_{tj} & a_{ijt} \end{vmatrix}. \end{align*} $$
$$ \begin{align*} (\delta_{G\setminus f}-I)^2(\mathbf{u}') = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}' \hspace{15pt} \text{where} \hspace{15pt} c_{rst}' = 2\sum_{1\leq i<j \leq g} \begin{vmatrix} q_{ri} & q_{rj} & a_{ijr} \\ q_{si} & q_{sj} & a_{ijs} \\ q_{ti} & q_{tj} & a_{ijt} \end{vmatrix}. \end{align*} $$
Next, let’s compute the difference
 $$ \begin{align*} &\mathbf{w}_{\tau'}(G\setminus f) - (\delta_{G\setminus f}-I)^2(\mathbf{u}') = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes (c_{rst} - c_{rst}'), \end{align*} $$
$$ \begin{align*} &\mathbf{w}_{\tau'}(G\setminus f) - (\delta_{G\setminus f}-I)^2(\mathbf{u}') = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes (c_{rst} - c_{rst}'), \end{align*} $$
where
 $$ \begin{align*} c_{rst} - c_{rst}' = 2\sum_{j=1}^g \begin{vmatrix} q_{r0} & q_{rj} & a_{0jr} \\ q_{s0} & q_{sj} & a_{0js} \\ q_{t0} & q_{tj} & a_{0jt} \end{vmatrix} \hspace{10pt} \text{for} \hspace{10pt} 1\leq r < s < t \leq g. \end{align*} $$
$$ \begin{align*} c_{rst} - c_{rst}' = 2\sum_{j=1}^g \begin{vmatrix} q_{r0} & q_{rj} & a_{0jr} \\ q_{s0} & q_{sj} & a_{0js} \\ q_{t0} & q_{tj} & a_{0jt} \end{vmatrix} \hspace{10pt} \text{for} \hspace{10pt} 1\leq r < s < t \leq g. \end{align*} $$
If we are in the first case, that is,
![]() $G=G_1$
and
$G=G_1$
and
![]() $f=a$
is a loop edge, then
$f=a$
is a loop edge, then
![]() $q_{j0}=0$
for
$q_{j0}=0$
for
![]() $j\geq 1$
, so the above formula implies
$j\geq 1$
, so the above formula implies
![]() $c_{rst}-c_{rst}' = 0$
, whence
$c_{rst}-c_{rst}' = 0$
, whence
![]() $\mathbf {w}_{\tau '}(G\setminus f) = (\delta _{G\setminus f}-I)^2(\mathbf {u}')$
.
$\mathbf {w}_{\tau '}(G\setminus f) = (\delta _{G\setminus f}-I)^2(\mathbf {u}')$
.
For the rest of the proof, suppose we are in the second case, that is,
![]() $G=G_2$
and
$G=G_2$
and
![]() $f=b=e_0$
is parallel to the edge
$f=b=e_0$
is parallel to the edge
![]() $c=e_1$
. Set
$c=e_1$
. Set
 $$ \begin{align*} \mathbf{u}"= \sum_{\substack{2\leq j \leq g\\ 1\leq k \leq g}} a_{0jk} \cdot \alpha_{1} \wedge \alpha_{j} \wedge \beta_{k}. \end{align*} $$
$$ \begin{align*} \mathbf{u}"= \sum_{\substack{2\leq j \leq g\\ 1\leq k \leq g}} a_{0jk} \cdot \alpha_{1} \wedge \alpha_{j} \wedge \beta_{k}. \end{align*} $$
We have
 $$ \begin{align*} (\delta_{G\setminus f} -I)^2(\mathbf{u}") = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}" \hspace{15pt} \text{where} \hspace{15pt} c_{rst}" = 2 \sum_{j=2}^g \begin{vmatrix} q_{r1} & q_{rj} & a_{0jr} \\ q_{s1} & q_{sj} & a_{0js} \\ q_{t1} & q_{tj} & a_{0jt} \end{vmatrix}. \end{align*} $$
$$ \begin{align*} (\delta_{G\setminus f} -I)^2(\mathbf{u}") = \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst}" \hspace{15pt} \text{where} \hspace{15pt} c_{rst}" = 2 \sum_{j=2}^g \begin{vmatrix} q_{r1} & q_{rj} & a_{0jr} \\ q_{s1} & q_{sj} & a_{0js} \\ q_{t1} & q_{tj} & a_{0jt} \end{vmatrix}. \end{align*} $$
When
![]() $r\geq 2$
, we have that
$r\geq 2$
, we have that
![]() $q_{r0} = q_{r1}$
, and therefore
$q_{r0} = q_{r1}$
, and therefore
![]() $c_{rst} - c_{rst}' = c_{rst}"$
. Now, consider
$c_{rst} - c_{rst}' = c_{rst}"$
. Now, consider
![]() $r=1$
. Since
$r=1$
. Since
![]() $x_0$
only appears in
$x_0$
only appears in
![]() $q_{00}$
, where
$q_{00}$
, where
![]() $q_{00} = x_{0} + q_{01}$
, the coefficient of
$q_{00} = x_{0} + q_{01}$
, the coefficient of
![]() $x_0$
in
$x_0$
in
![]() $c_{rst}$
must equal 0 for all
$c_{rst}$
must equal 0 for all
![]() $0\leq r<s<t\leq g$
by formula (5.1). By extracting the coefficient of
$0\leq r<s<t\leq g$
by formula (5.1). By extracting the coefficient of
![]() $x_0$
in the expression of
$x_0$
in the expression of
![]() $c_{0st}$
from formula (5.2), we see that
$c_{0st}$
from formula (5.2), we see that
 $$ \begin{align} \sum_{j=1}^{g} \begin{vmatrix} q_{sj} & a_{0js} \\ q_{tj} & a_{0jt} \end{vmatrix} = 0. \end{align} $$
$$ \begin{align} \sum_{j=1}^{g} \begin{vmatrix} q_{sj} & a_{0js} \\ q_{tj} & a_{0jt} \end{vmatrix} = 0. \end{align} $$
Therefore,
 $$ \begin{align*} c_{1st}" - (c_{1st} - c_{1st}') = 2 (q_{11}-q_{10}) \sum_{j=1}^g \begin{vmatrix} q_{sj} & a_{0js} \\ q_{tj} & a_{0jt} \end{vmatrix} =0, \end{align*} $$
$$ \begin{align*} c_{1st}" - (c_{1st} - c_{1st}') = 2 (q_{11}-q_{10}) \sum_{j=1}^g \begin{vmatrix} q_{sj} & a_{0js} \\ q_{tj} & a_{0jt} \end{vmatrix} =0, \end{align*} $$
where the last equality follows from formula (5.3). So
![]() $c_{rst} = c_{rst}' + c_{rst}"$
and therefore
$c_{rst} = c_{rst}' + c_{rst}"$
and therefore
 $$ \begin{align*} \mathbf{w}_{\tau'}(G\setminus f) &=\sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst} \\ &= \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes (c_{rst}' + c_{rst}") = (\delta_{G\setminus f}-I)^2(\mathbf{u}' + \mathbf{u}").\\[-44pt] \end{align*} $$
$$ \begin{align*} \mathbf{w}_{\tau'}(G\setminus f) &=\sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes c_{rst} \\ &= \sum_{1\leq r<s<t \leq g} \beta_{r} \wedge \beta_{s} \wedge \beta_{t} \otimes (c_{rst}' + c_{rst}") = (\delta_{G\setminus f}-I)^2(\mathbf{u}' + \mathbf{u}").\\[-44pt] \end{align*} $$
Next, we show that Ceresa–Zharkov triviality may be detected at the level of
![]() $2$
-connected components.
$2$
-connected components.
Proposition 5.5. A connected graph G is Ceresa–Zharkov trivial if and only if its 2-connected components are Ceresa–Zharkov trivial.
Proof. By induction, it suffices to consider the case where G has two 2-connected components
![]() $G_1$
and
$G_1$
and
![]() $G_2$
. Choose a separating curve
$G_2$
. Choose a separating curve
![]() $\gamma $
and an arrangement of simple closed curves
$\gamma $
and an arrangement of simple closed curves
![]() $\Lambda = \{\ell _e \, : \, e\in E(G) \}$
such that
$\Lambda = \{\ell _e \, : \, e\in E(G) \}$
such that
-
- the dual graph of
 $\Lambda $
is G;
$\Lambda $
is G; -
- cutting along
 $\gamma $
separates
$\gamma $
separates
 $\Sigma _g$
into two subsurfaces
$\Sigma _g$
into two subsurfaces
 $S_1\cong \Sigma _{g_1}^1$
and
$S_1\cong \Sigma _{g_1}^1$
and
 $S_2 \cong \Sigma _{g_2}^1$
;
$S_2 \cong \Sigma _{g_2}^1$
; -
-
 $\ell _e$
lies in
$\ell _e$
lies in
 $S_i$
whenever
$S_i$
whenever
 $e\in E(G_i)$
.
$e\in E(G_i)$
.
Denote by
![]() $H^{(i)} = H_1(\Sigma _{g_i}, \mathbb {Z})$
and
$H^{(i)} = H_1(\Sigma _{g_i}, \mathbb {Z})$
and
![]() $L^{(i)} = \wedge ^3H^{(i)}$
. The inclusion
$L^{(i)} = \wedge ^3H^{(i)}$
. The inclusion
![]() $S_i\subset \Sigma _g$
allows us to view
$S_i\subset \Sigma _g$
allows us to view
![]() $F_qL^{(i)} \otimes R$
as an R-submodule of
$F_qL^{(i)} \otimes R$
as an R-submodule of
![]() $F_qL_R$
for
$F_qL_R$
for
![]() $q=0,\ldots ,3$
. Choose hyperelliptic quasi-involutions
$q=0,\ldots ,3$
. Choose hyperelliptic quasi-involutions
![]() $\tau _1'$
of
$\tau _1'$
of
![]() $S_1$
and
$S_1$
and
![]() $\tau _2'$
of
$\tau _2'$
of
![]() $S_2$
such that
$S_2$
such that
![]() $\boldsymbol \mu _{\tau _i'}(\Lambda _i')$
lies in
$\boldsymbol \mu _{\tau _i'}(\Lambda _i')$
lies in
![]() $F_2L^{(i)} \otimes R_1$
; this is possible by Proposition 4.1. Let
$F_2L^{(i)} \otimes R_1$
; this is possible by Proposition 4.1. Let
![]() $\tau $
be the hyperelliptic quasi-involution of
$\tau $
be the hyperelliptic quasi-involution of
![]() $\Sigma _g$
obtained that restricts to
$\Sigma _g$
obtained that restricts to
![]() $\tau _i'$
on
$\tau _i'$
on
![]() $S_i$
. Denote by
$S_i$
. Denote by
![]() $\tau _i\in \operatorname {\mathrm {Mod}}(\Sigma _{g_i})$
the image of
$\tau _i\in \operatorname {\mathrm {Mod}}(\Sigma _{g_i})$
the image of
![]() $\tau '$
under the natural map
$\tau '$
under the natural map
![]() $\operatorname {\mathrm {Mod}}(\Sigma _{g_i}^1) \to \operatorname {\mathrm {Mod}}(\Sigma _{g_i})$
; thus
$\operatorname {\mathrm {Mod}}(\Sigma _{g_i}^1) \to \operatorname {\mathrm {Mod}}(\Sigma _{g_i})$
; thus
![]() $\tau _i$
is a hyperelliptic quasi-involution of
$\tau _i$
is a hyperelliptic quasi-involution of
![]() $\Sigma _{g_i}$
. Then
$\Sigma _{g_i}$
. Then
![]() $\mathbf {v}_{\tau _1}(G_1), \mathbf {v}_{\tau _2}(G_2), \mathbf {v}_{\tau }(G)$
are in
$\mathbf {v}_{\tau _1}(G_1), \mathbf {v}_{\tau _2}(G_2), \mathbf {v}_{\tau }(G)$
are in
![]() $F_2L\otimes R_1$
, and therefore
$F_2L\otimes R_1$
, and therefore
![]() $\mathbf {w}_{\tau _1}(G_1), \mathbf {w}_{\tau _2}(G_2), \mathbf {w}_{\tau }(G)$
are in
$\mathbf {w}_{\tau _1}(G_1), \mathbf {w}_{\tau _2}(G_2), \mathbf {w}_{\tau }(G)$
are in
![]() $F_3L\otimes R_2$
.
$F_3L\otimes R_2$
.
Consider the following commutative diagram:

The right arrow on the bottom row is an isomorphism by formula (2.1). Consider
![]() $\boldsymbol \mu := \boldsymbol \mu _{\tau _1'}(\Lambda _1') + \boldsymbol \mu _{\tau _2'}(\Lambda _2')$
in
$\boldsymbol \mu := \boldsymbol \mu _{\tau _1'}(\Lambda _1') + \boldsymbol \mu _{\tau _2'}(\Lambda _2')$
in
![]() $(F_2L^{(1)} \oplus F_2L^{(2)})_R$
. The composition of the top two arrows of the diagram in Equation (5.4) maps
$(F_2L^{(1)} \oplus F_2L^{(2)})_R$
. The composition of the top two arrows of the diagram in Equation (5.4) maps
![]() $\boldsymbol \mu $
to
$\boldsymbol \mu $
to
![]() $\mathbf {v}_{\tau }(G)$
, which maps to
$\mathbf {v}_{\tau }(G)$
, which maps to
![]() $\mathbf {w}_{\tau }(G)$
by the right vertical arrow. The composition along the bottom takes
$\mathbf {w}_{\tau }(G)$
by the right vertical arrow. The composition along the bottom takes
![]() $\boldsymbol \mu $
to
$\boldsymbol \mu $
to
![]() $\mathbf {w}_{\tau _1}(G_1) + \mathbf {w}_{\tau _2}(G_2)$
. Thus,
$\mathbf {w}_{\tau _1}(G_1) + \mathbf {w}_{\tau _2}(G_2)$
. Thus,
Suppose
![]() $G_1$
and
$G_1$
and
![]() $G_2$
are Ceresa–Zharkov trivial. By Proposition 4.2, there are elements
$G_2$
are Ceresa–Zharkov trivial. By Proposition 4.2, there are elements
![]() $\mathbf {u}_i\in F_1(L^{(i)}/H^{(i)})$
such that
$\mathbf {u}_i\in F_1(L^{(i)}/H^{(i)})$
such that
![]() $(\delta _{G_i}-I)^2(\mathbf {u}_i) = \mathbf {w}_{\tau _i}(G_i)$
. The restriction of
$(\delta _{G_i}-I)^2(\mathbf {u}_i) = \mathbf {w}_{\tau _i}(G_i)$
. The restriction of
![]() $(\delta _G-I)^2$
to
$(\delta _G-I)^2$
to
![]() $F_1L^{(1)} \oplus F_1L^{(2)}$
is
$F_1L^{(1)} \oplus F_1L^{(2)}$
is
![]() $(\delta _{G_1}-I)^2 \oplus (\delta _{G_2}-I)^2$
; this follows from formula (3.6) and the fact that
$(\delta _{G_1}-I)^2 \oplus (\delta _{G_2}-I)^2$
; this follows from formula (3.6) and the fact that
![]() $Q_G = Q_{G_1}\oplus Q_{G_2}$
. So
$Q_G = Q_{G_1}\oplus Q_{G_2}$
. So
![]() $(\delta _{G}-I)^2(\mathbf {u}_1+\mathbf {u}_2) = \mathbf {w}_{\tau }(G)$
, and therefore G is Ceresa–Zharkov trivial.
$(\delta _{G}-I)^2(\mathbf {u}_1+\mathbf {u}_2) = \mathbf {w}_{\tau }(G)$
, and therefore G is Ceresa–Zharkov trivial.
Conversely, suppose G is Ceresa–Zharkov trivial. Let T be a spanning tree of
![]() $G_1$
. Then
$G_1$
. Then
![]() $G/T$
is Ceresa–Zharkov trivial by Proposition 4.4. Observe that
$G/T$
is Ceresa–Zharkov trivial by Proposition 4.4. Observe that
![]() $G/T$
is obtained from
$G/T$
is obtained from
![]() $G_2$
by attaching
$G_2$
by attaching
![]() $g_1$
loop edges to a single vertex of
$g_1$
loop edges to a single vertex of
![]() $G_2$
. So
$G_2$
. So
![]() $G_2$
is Ceresa–Zharkov trivial by Proposition 5.1. Swapping the roles of
$G_2$
is Ceresa–Zharkov trivial by Proposition 5.1. Swapping the roles of
![]() $G_1$
and
$G_1$
and
![]() $G_2$
, we conclude that
$G_2$
, we conclude that
![]() $G_1$
is also Ceresa–Zharkov trivial.
$G_1$
is also Ceresa–Zharkov trivial.
Recall from [Reference Corey9, §3] that a graph G is strongly of hyperelliptic type if there is a choice of edge lengths of G so that the resulting tropical curve is hyperelliptic. Such graphs are Ceresa–Zharkov trivial by the following proposition.
Proposition 5.6. Let G be a graph that has a separating pair of edges
![]() $(f,f')$
, and let
$(f,f')$
, and let
![]() $\Lambda = \{\ell _e \, : \, e\in E(G)\}$
be a collection of pairwise disjoint simple closed curves on
$\Lambda = \{\ell _e \, : \, e\in E(G)\}$
be a collection of pairwise disjoint simple closed curves on
![]() $\Sigma _g$
with dual graph G. If
$\Sigma _g$
with dual graph G. If
![]() $\tau $
is a hyperelliptic quasi-involution such that
$\tau $
is a hyperelliptic quasi-involution such that
![]() $\tau (\ell _{f}) = \ell _{f'}$
, then
$\tau (\ell _{f}) = \ell _{f'}$
, then
In particular, if G is strongly of hyperelliptic type, then G is Ceresa–Zharkov trivial.
Proof. The removal of
![]() $\{f,f'\}$
from G separates this graph into two graphs
$\{f,f'\}$
from G separates this graph into two graphs
![]() $G_1$
and
$G_1$
and
![]() $G_2$
of gerena
$G_2$
of gerena
![]() $g_1$
and
$g_1$
and
![]() $g_2$
, respectively. Order the edges of G by
$g_2$
, respectively. Order the edges of G by
![]() $e_1, \ldots , e_g, e_{g+1}, \ldots , e_{n}$
so that
$e_1, \ldots , e_g, e_{g+1}, \ldots , e_{n}$
so that
-
-
 $e_1,\ldots ,e_{g_1} \in E(G_1)$
,
$e_1,\ldots ,e_{g_1} \in E(G_1)$
,
 $e_{g_1+1},\ldots ,e_{g-1} \in E(G_2)$
, and
$e_{g_1+1},\ldots ,e_{g-1} \in E(G_2)$
, and
 $e_{g} = f$
;
$e_{g} = f$
; -
-
 $e_{g+1}, \ldots , e_{n}$
are the edges of a spanning tree of G.
$e_{g+1}, \ldots , e_{n}$
are the edges of a spanning tree of G.
Necessarily,
![]() $f'$
must be among the edges of the spanning tree. Let
$f'$
must be among the edges of the spanning tree. Let
![]() $\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$
be the basis from §3.3. With respect to this basis, we have
$\alpha _1,\ldots ,\alpha _g,\beta _1,\ldots ,\beta _g$
be the basis from §3.3. With respect to this basis, we have
 $$ \begin{align*} Q_G = \begin{bmatrix} Q_{G_1} & 0 & * \\ 0 & Q_{G_2} & * \\ * & * & x_{f} \end{bmatrix}. \end{align*} $$
$$ \begin{align*} Q_G = \begin{bmatrix} Q_{G_1} & 0 & * \\ 0 & Q_{G_2} & * \\ * & * & x_{f} \end{bmatrix}. \end{align*} $$
Cutting along
![]() $\ell _{f}$
and
$\ell _{f}$
and
![]() $\ell _{f'}$
separates the surface
$\ell _{f'}$
separates the surface
![]() $\Sigma _g$
into two subsurfaces
$\Sigma _g$
into two subsurfaces
![]() $S_1$
and
$S_1$
and
![]() $S_2$
. The homology of
$S_2$
. The homology of
![]() $S_i$
splits as a direct sum
$S_i$
splits as a direct sum
![]() $V\oplus W_i$
, where
$V\oplus W_i$
, where
![]() $V = \mathbb {Z} \cdot [\ell _f]$
and
$V = \mathbb {Z} \cdot [\ell _f]$
and
![]() $W_i$
is identified with a symplectic subspace of H under the map
$W_i$
is identified with a symplectic subspace of H under the map
![]() $H_1(S_i,\mathbb {Z}) \to H$
. The intersection 2-form
$H_1(S_i,\mathbb {Z}) \to H$
. The intersection 2-form
![]() $\omega _i$
of
$\omega _i$
of
![]() $W_i$
is the restriction of
$W_i$
is the restriction of
![]() $\omega $
to
$\omega $
to
![]() $W_i$
, so
$W_i$
, so
 $$ \begin{align*} \omega_1 = \sum_{j=1}^{g_1} \alpha_j \wedge \beta_j \hspace{15pt} \text{and} \hspace{15pt} \omega_2 = \sum_{j=g_1+1}^{g-1} \alpha_j \wedge \beta_j. \end{align*} $$
$$ \begin{align*} \omega_1 = \sum_{j=1}^{g_1} \alpha_j \wedge \beta_j \hspace{15pt} \text{and} \hspace{15pt} \omega_2 = \sum_{j=g_1+1}^{g-1} \alpha_j \wedge \beta_j. \end{align*} $$
Orient
![]() $[\ell _{f}]$
such that
$[\ell _{f}]$
such that
![]() $S_1$
lies to its right. Because
$S_1$
lies to its right. Because
![]() $\tau (\ell _{f}) = \ell _{f'}$
, we have that
$\tau (\ell _{f}) = \ell _{f'}$
, we have that
![]() $\tau T_{\ell _{f}} \tau ^{-1} = T_{\ell _{f'}}$
, and hence
$\tau T_{\ell _{f}} \tau ^{-1} = T_{\ell _{f'}}$
, and hence
The expression
![]() $(\delta _{G}-I)(J(T_{\ell _{f}} T_{\ell _{f'}}^{-1}))$
is equal to
$(\delta _{G}-I)(J(T_{\ell _{f}} T_{\ell _{f'}}^{-1}))$
is equal to
 $$ \begin{align*} (\delta_{G}-I)(\omega_1\wedge [\ell_{f}]) = \sum_{j=1}^{g_1} (Q_{G} \, \alpha_j ) \wedge \beta_j \wedge \beta_g = \sum_{j=1}^{g_1} (Q_{G_1} \, \alpha_j ) \wedge \beta_j \wedge \beta_g = (\delta_{G_1}-I)(\omega_1\wedge [\ell_{f}]). \end{align*} $$
$$ \begin{align*} (\delta_{G}-I)(\omega_1\wedge [\ell_{f}]) = \sum_{j=1}^{g_1} (Q_{G} \, \alpha_j ) \wedge \beta_j \wedge \beta_g = \sum_{j=1}^{g_1} (Q_{G_1} \, \alpha_j ) \wedge \beta_j \wedge \beta_g = (\delta_{G_1}-I)(\omega_1\wedge [\ell_{f}]). \end{align*} $$
We use formula (3.6) in the first equality and
![]() $Q_{G}(\alpha _j) - Q_{G_1}(\alpha _j) \in \mathbb {Z}\cdot \beta _g$
for
$Q_{G}(\alpha _j) - Q_{G_1}(\alpha _j) \in \mathbb {Z}\cdot \beta _g$
for
![]() $j\leq g_1$
in the second. By Proposition 3.3 applied to V and
$j\leq g_1$
in the second. By Proposition 3.3 applied to V and
![]() $W=W_1$
, we have
$W=W_1$
, we have
for some
![]() $\eta \in V\wedge W_1$
. Since the curves in
$\eta \in V\wedge W_1$
. Since the curves in
![]() $\Lambda $
are disjoint, we have that
$\Lambda $
are disjoint, we have that
![]() $\delta _{G_1}([\ell _f]) = [\ell _{f}]$
. This implies that the first summand above is 0, and the second summand is in
$\delta _{G_1}([\ell _f]) = [\ell _{f}]$
. This implies that the first summand above is 0, and the second summand is in
![]() $V\wedge W_1\wedge V$
, which must also be 0 since
$V\wedge W_1\wedge V$
, which must also be 0 since
![]() $\dim V = 1$
. So we have
$\dim V = 1$
. So we have
![]() $(\delta _{G}-I)(J([T_{\ell _{f}}, \tau ])) = 0$
, as required.
$(\delta _{G}-I)(J([T_{\ell _{f}}, \tau ])) = 0$
, as required.
Now, suppose G is strongly of hyperelliptic type. By Proposition 4.7, we may assume that G is stable. Let
![]() $\Gamma $
be a hyperelliptic tropical curve with underlying graph G, and
$\Gamma $
be a hyperelliptic tropical curve with underlying graph G, and
![]() $\sigma $
be a hyperelliptic involution of
$\sigma $
be a hyperelliptic involution of
![]() $\Gamma $
. There is a hyperelliptic quasi-involution
$\Gamma $
. There is a hyperelliptic quasi-involution
![]() $\tau $
of
$\tau $
of
![]() $\Sigma _g$
such that
$\Sigma _g$
such that
![]() $\tau (\ell _{e}) = \ell _{\sigma (e)}$
by [Reference Corey, Ellenberg and Li10, Lemma 4.5]. By [Reference Corey9, Proposition 2.5], for any edge
$\tau (\ell _{e}) = \ell _{\sigma (e)}$
by [Reference Corey, Ellenberg and Li10, Lemma 4.5]. By [Reference Corey9, Proposition 2.5], for any edge
![]() $e\in E(G)$
, we have that
$e\in E(G)$
, we have that
![]() $\sigma (e) = e$
or
$\sigma (e) = e$
or
![]() $\sigma (e) = f$
, where
$\sigma (e) = f$
, where
![]() $(e,f)$
is a separating pair. In the first case,
$(e,f)$
is a separating pair. In the first case,
![]() $[T_{\ell _e},\tau ] = 1$
. In the second case,
$[T_{\ell _e},\tau ] = 1$
. In the second case,
![]() $(\delta _G-I)(J([T_{\ell _e},\tau ])) = 0$
by the first part of this proposition. We conclude that
$(\delta _G-I)(J([T_{\ell _e},\tau ])) = 0$
by the first part of this proposition. We conclude that
![]() $\mathbf {w}_{\tau }(G) = 0$
, that is, G is Ceresa–Zharkov trivial.
$\mathbf {w}_{\tau }(G) = 0$
, that is, G is Ceresa–Zharkov trivial.
To prove Ceresa–Zharkov trivial implies hyperelliptic type, we use in an essential way the main theorem of [Reference Corey9], which states that a graph is of hyperelliptic type if and only if it has no
![]() $K_4$
or
$K_4$
or
![]() $L_3$
minor. We prove directly that these graphs are not Ceresa–Zharkov trivial, using Proposition 4.8.
$L_3$
minor. We prove directly that these graphs are not Ceresa–Zharkov trivial, using Proposition 4.8.
Proposition 5.7. The graph
![]() $G=K_4$
is not Ceresa–Zharkov trivial.
$G=K_4$
is not Ceresa–Zharkov trivial.
Proof. By [Reference Corey, Ellenberg and Li10, Example 7.2], a Ceresa cocycle
![]() $\mathbf {v}_{\tau }(G)$
for the graph
$\mathbf {v}_{\tau }(G)$
for the graph
![]() $K_4$
is given by
$K_4$
is given by
which lies in
![]() $F_2(L/H) \otimes R_1$
. The matrix
$F_2(L/H) \otimes R_1$
. The matrix
![]() $Q_G$
is recorded in formula (3.5). We get
$Q_G$
is recorded in formula (3.5). We get
which lies in
![]() $F_3(L/H) \otimes R_2$
. By Proposition 4.8, it is sufficient to show that the tropical curve
$F_3(L/H) \otimes R_2$
. By Proposition 4.8, it is sufficient to show that the tropical curve
![]() $\Gamma = (K_4,c)$
is not Ceresa–Zharkov trivial for some edge-length function
$\Gamma = (K_4,c)$
is not Ceresa–Zharkov trivial for some edge-length function
![]() $c:E(K_4) \to \mathbb {Z}_{>0}$
. Let c be the function that assigns the length 1 to each edge. Then
$c:E(K_4) \to \mathbb {Z}_{>0}$
. Let c be the function that assigns the length 1 to each edge. Then
![]() $\mathbf {w}(\Gamma ) = -2 \, \beta _{1} \wedge \beta _{2} \wedge \beta _{3} $
, whereas
$\mathbf {w}(\Gamma ) = -2 \, \beta _{1} \wedge \beta _{2} \wedge \beta _{3} $
, whereas
![]() $(\delta _{\Gamma }-I)^2(F_1(L/H))$
is spanned by
$(\delta _{\Gamma }-I)^2(F_1(L/H))$
is spanned by
![]() $4\, \beta _{1} \wedge \beta _{2} \wedge \beta _{3} $
; see [Reference Corey, Ellenberg and Li10, Remark 7.3]. So
$4\, \beta _{1} \wedge \beta _{2} \wedge \beta _{3} $
; see [Reference Corey, Ellenberg and Li10, Remark 7.3]. So
![]() $\mathbf {w}(\Gamma ) \neq 0$
, as required.
$\mathbf {w}(\Gamma ) \neq 0$
, as required.
Remark 5.8. Define
![]() $c:E(K_4) \to \mathbb {Z}_{>0}$
by
$c:E(K_4) \to \mathbb {Z}_{>0}$
by
![]() $c(e_1) = 2$
and
$c(e_1) = 2$
and
![]() $c(e_i)=1$
for
$c(e_i)=1$
for
![]() $i=2,\ldots ,6$
, and let
$i=2,\ldots ,6$
, and let
![]() $\Gamma =(K_4,c)$
. Then
$\Gamma =(K_4,c)$
. Then
![]() $(\delta _{\Gamma }-I)^2(F_1(L/H)) = F_3L$
, and hence
$(\delta _{\Gamma }-I)^2(F_1(L/H)) = F_3L$
, and hence
![]() $\mathbf {w}(\Gamma ) = 0$
. Therefore,
$\mathbf {w}(\Gamma ) = 0$
. Therefore,
![]() $\Gamma $
is Ceresa–Zharkov trivial but clearly not of hyperelliptic type.
$\Gamma $
is Ceresa–Zharkov trivial but clearly not of hyperelliptic type.
Proposition 5.9. The graph
![]() $G=L_3$
is not Ceresa–Zharkov trivial.
$G=L_3$
is not Ceresa–Zharkov trivial.
Proof. From [Reference Corey, Ellenberg and Li10, Example 7.6] by setting
![]() $c_7=c_8=c_9=0$
, we get
$c_7=c_8=c_9=0$
, we get
 $$ \begin{align*} Q_G = \begin{pmatrix} x_1 + x_6 & 0 & x_6 & x_6 \\ 0 & x_2+x_5 & x_5 & x_5 \\ x_6 & x_5 & x_3+x_5+x_6 & x_5+x_6 \\ x_6 & x_5 & x_5+x_6 & x_4+x_5+x_6 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} Q_G = \begin{pmatrix} x_1 + x_6 & 0 & x_6 & x_6 \\ 0 & x_2+x_5 & x_5 & x_5 \\ x_6 & x_5 & x_3+x_5+x_6 & x_5+x_6 \\ x_6 & x_5 & x_5+x_6 & x_4+x_5+x_6 \end{pmatrix}. \end{align*} $$
 $$ \begin{align*} \mathbf{v}_{\tau}(G)= &(\alpha_{2} \wedge \beta_{2} \wedge \beta_{3} + \alpha_{2} \wedge \beta_{2} \wedge \beta_{4} -\alpha_{2} \wedge \beta_{1} \wedge \beta_{2} ) \otimes x_6 \\ -&(\alpha_{1} \wedge \beta_{1} \wedge \beta_{2} + \alpha_{1} \wedge \beta_{1} \wedge \beta_{3} + \alpha_{1} \wedge \beta_{1} \wedge \beta_{4} )\otimes x_5. \end{align*} $$
$$ \begin{align*} \mathbf{v}_{\tau}(G)= &(\alpha_{2} \wedge \beta_{2} \wedge \beta_{3} + \alpha_{2} \wedge \beta_{2} \wedge \beta_{4} -\alpha_{2} \wedge \beta_{1} \wedge \beta_{2} ) \otimes x_6 \\ -&(\alpha_{1} \wedge \beta_{1} \wedge \beta_{2} + \alpha_{1} \wedge \beta_{1} \wedge \beta_{3} + \alpha_{1} \wedge \beta_{1} \wedge \beta_{4} )\otimes x_5. \end{align*} $$
So we have
By Proposition 4.8, it is sufficient to show that the tropical curve
![]() $\Gamma = (L_3,c)$
is not Ceresa–Zharkov trivial for some edge-length function
$\Gamma = (L_3,c)$
is not Ceresa–Zharkov trivial for some edge-length function
![]() $c:E(L_3) \to \mathbb {Z}_{>0}$
. Let c be the function that assigns the length 1 to each edge. Using OSCAR [Reference Eder, Decker, Fieker, Horn and Joswig11, 15] (which runs in julia [Reference Bezanson, Edelman, Karpinski and Shah3]), we show that
$c:E(L_3) \to \mathbb {Z}_{>0}$
. Let c be the function that assigns the length 1 to each edge. Using OSCAR [Reference Eder, Decker, Fieker, Horn and Joswig11, 15] (which runs in julia [Reference Bezanson, Edelman, Karpinski and Shah3]), we show that
![]() $(\delta _{\Gamma }-I)^2(F_1(L/H))$
is spanned by
$(\delta _{\Gamma }-I)^2(F_1(L/H))$
is spanned by
The code may be found in the github repositoryhttps://github.com/dcorey2814/ceresaZharkovClassOne readily verifies that
![]() $\mathbf {w}_{\tau }(\Gamma ) = -2\beta _{1} \wedge \beta _{2} \wedge \beta _{3} -2 \beta _{1} \wedge \beta _{2} \wedge \beta _{4} $
and
$\mathbf {w}_{\tau }(\Gamma ) = -2\beta _{1} \wedge \beta _{2} \wedge \beta _{3} -2 \beta _{1} \wedge \beta _{2} \wedge \beta _{4} $
and
![]() $\mathbf {w}_{\tau }(\Gamma )$
is not in the
$\mathbf {w}_{\tau }(\Gamma )$
is not in the
![]() $\mathbb {Z}$
-span of the vectors listed above. So
$\mathbb {Z}$
-span of the vectors listed above. So
![]() $L_3$
is not Ceresa–Zharkov trivial.
$L_3$
is not Ceresa–Zharkov trivial.
Lemma 5.10. Suppose G is a graph with a minor
![]() $G'$
obtained by adding (parallel) edges to the complete graph
$G'$
obtained by adding (parallel) edges to the complete graph
![]() $K_m$
. Then there are edges
$K_m$
. Then there are edges
![]() $S_1\subset E(G)$
and
$S_1\subset E(G)$
and
![]() $S_2 \subset E(G/S_1)$
such that
$S_2 \subset E(G/S_1)$
such that
![]() $(G/S_1) \setminus S_2$
is
$(G/S_1) \setminus S_2$
is
![]() $G'$
, and every edge in
$G'$
, and every edge in
![]() $S_2$
is either a loop or parallel to another edge in
$S_2$
is either a loop or parallel to another edge in
![]() $G/S_1$
.
$G/S_1$
.
Proof. The order in which edges are contracted or removed does not matter when forming a graph minor, so suppose
![]() $G' = (G/S_1) \setminus S_2$
. As contracting an edge drops the number of vertices by one and removing an edge preserves the number of vertices, we have that
$G' = (G/S_1) \setminus S_2$
. As contracting an edge drops the number of vertices by one and removing an edge preserves the number of vertices, we have that
![]() $V(G/S_1) = V(G')$
. As there is an edge between any two vertices in
$V(G/S_1) = V(G')$
. As there is an edge between any two vertices in
![]() $G'$
, every edge in
$G'$
, every edge in
![]() $S_1$
must be either a loop or parallel to some other edge.
$S_1$
must be either a loop or parallel to some other edge.
Theorem 5.11. A connected graph G is Ceresa–Zharkov trivial if and only if it is of hyperelliptic type.
Proof. Suppose G is not of hyperelliptic type. By [Reference Corey9, Theorem 1.1], G has a
![]() $K_4$
or
$K_4$
or
![]() $L_3$
minor. By Lemma 5.10, there are subsets
$L_3$
minor. By Lemma 5.10, there are subsets
![]() $S_1\subset E(G)$
and
$S_1\subset E(G)$
and
![]() $S_2\subset E(G/S_1)$
such that
$S_2\subset E(G/S_1)$
such that
![]() $(G/S_1) \setminus S_2$
is
$(G/S_1) \setminus S_2$
is
![]() $K_4$
or
$K_4$
or
![]() $L_3$
, and every edge of
$L_3$
, and every edge of
![]() $S_2$
is a loop or parallel to another edge in
$S_2$
is a loop or parallel to another edge in
![]() $G/S_1$
. The graph
$G/S_1$
. The graph
![]() $(G/S_1) \setminus S_2$
is not Ceresa–Zharkov trivial by Propositions 5.7 and 5.9. So
$(G/S_1) \setminus S_2$
is not Ceresa–Zharkov trivial by Propositions 5.7 and 5.9. So
![]() $(G/S_1)$
is not Ceresa–Zharkov trivial by Propositions 5.1 and 5.5, and therefore G is not Ceresa–Zharkov trivial by Proposition 4.4.
$(G/S_1)$
is not Ceresa–Zharkov trivial by Propositions 5.1 and 5.5, and therefore G is not Ceresa–Zharkov trivial by Proposition 4.4.
For the converse, first suppose that G is of hyperelliptic type and 2-connected. By [Reference Corey9, Theorem 4.5], there is a
![]() $\tilde {G}$
that is strongly of hyperelliptic type such that
$\tilde {G}$
that is strongly of hyperelliptic type such that
![]() $G = \tilde {G}/S$
for some subset
$G = \tilde {G}/S$
for some subset
![]() $S\subset E(G)$
. The graph
$S\subset E(G)$
. The graph
![]() $\tilde {G}$
is Ceresa–Zharkov trivial by Proposition 5.6, and therefore so is G by Proposition 4.4.
$\tilde {G}$
is Ceresa–Zharkov trivial by Proposition 5.6, and therefore so is G by Proposition 4.4.
In general, if G is of hyperelliptic type, then its 2-connected components are of hyperelliptic type, and hence Ceresa–Zharkov trivial. The graph G is Ceresa–Zharkov trivial by Proposition 5.5.
Corollary 5.12. The property of being Ceresa–Zharkov trivial is a minor closed condition on graphs.
Proof. This follows from Theorem 5.11 and the fact that being of hyperelliptic type is a minor closed condition on graphs [Reference Corey9, Proposition 3.8].
Acknowledgements
We thank Jordan Ellenberg for helpful discussions, especially at the beginning of this project, and the referee for their valuable feedback and comments.
Competing interest
The authors have no competing interest to declare.
Funding statement
DC was supported by NSF-RTG grant 1502553 and the SFB-TRR project ‘Symbolic Tools in Mathematics and their Application’ (project-ID 286237555). WL was supported by the Centre de Recherches Mathématiques- Institut des Sciences Mathématiques postdoctoral fellowship.