Hostname: page-component-848d4c4894-p2v8j Total loading time: 0.001 Render date: 2024-06-02T14:50:35.725Z Has data issue: false hasContentIssue false
  • English
  • Français

HILBERT STRATIFOLDS AND A QUILLEN TYPE GEOMETRIC DESCRIPTION OF COHOMOLOGY FOR HILBERT MANIFOLDS

Part of: Infinite-dimensional manifolds Differential topology

Published online by Cambridge University Press:  27 February 2018

MATTHIAS KRECK  and
HAGGAI TENE
MATTHIAS KRECK
Affiliation:
Max-Planck Institut & Mathematisches Institut, Rheinische Friedrich-Wilhelms-Universität, Bonn, Germany; kreck@math.uni-bonn.de
HAGGAI TENE
Affiliation:
Mathematisches Institut, Universität Heidelberg; tene@mathi.uni-heidelberg.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we use tools from differential topology to give a geometric description of cohomology for Hilbert manifolds. Our model is Quillen’s geometric description of cobordism groups for finite-dimensional smooth manifolds [Quillen, ‘Elementary proofs of some results of cobordism theory using steenrod operations’, Adv. Math., 7 (1971)]. Quillen stresses the fact that this construction allows the definition of Gysin maps for ‘oriented’ proper maps. For finite-dimensional manifolds one has a Gysin map in singular cohomology which is based on Poincaré duality, hence it is not clear how to extend it to infinite-dimensional manifolds. But perhaps one can overcome this difficulty by giving a Quillen type description of singular cohomology for Hilbert manifolds. This is what we do in this paper. Besides constructing a general Gysin map, one of our motivations was a geometric construction of equivariant cohomology, which even for a point is the cohomology of the infinite-dimensional space 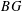$BG$, which has a Hilbert manifold model. Besides that, we demonstrate the use of such a geometric description of cohomology by several other applications. We give a quick description of characteristic classes of a finite-dimensional vector bundle and apply it to a generalized Steenrod representation problem for Hilbert manifolds and define a notion of a degree of proper oriented Fredholm maps of index 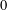$0$.

MSC classification

Primary: 58B05: Homotopy and topological questions
Secondary: 57R19: Algebraic topology on manifolds
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e4
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2018

References

Atiyah, M. F., K-theory, Lecture notes by D. W. Anderson (W. A. Benjamin, Inc., New York–Amsterdam, 1967).Google Scholar
Baker, A. and Özel, C., ‘Complex cobordism of Hilbert manifolds with some applications to flag varieties of loop groups’, in(English Summary) Geometry and Topology: Aarhus (1998), Contemporary Mathematics, 258 (American Mathematical Society, Providence, RI, 2000), 1–19.Google Scholar
Burghelea, D. and Henderson, D., ‘Smoothings and homeomorphisms for Hilbert manifolds’, Bull. Amer. Math. Soc. (N.S.) 76 (1970).CrossRefGoogle Scholar
Burghelea, D. and Kuiper, N. H., ‘Hilbert manifolds’, Ann. of Math. (2) 90(3) (1969), 379–417.CrossRefGoogle Scholar
Conner, P. E. and Floyd, E. E., Differentiable Periodic Maps, Ergebnisse der Mathematik und ihrer Grenzgebiete, N. F., Band 33 (Academic Press Inc., Springer, Berlin–Göttingen–Heidelberg, New York, 1964).Google Scholar
Dold, A., Geometric Cobordism and the Fixed Point Transfer, Lecture Notes in Mathematics (Springer, Berlin, 1976).Google Scholar
Eells, J., Fibring Spaces of Maps, Symposium on Infinite-Dimensional Topology (Louisiana State University, Baton Rouge, LA, 1967), Annals of Mathematics Studies, 69 (Princeton University Press, Princeton, NJ, 1972), 43–57.Google Scholar
Eells, J., ‘A setting for global analysis’, Bull. Amer. Math. Soc. (N.S.) 72 (1966), 751–807.CrossRefGoogle Scholar
Eells, J. and Elworthy, K. D., ‘Open embeddings of certain Banach manifolds’, Ann. of Math. (2) 91(3) (1970).CrossRefGoogle Scholar
Elworthy, K. D. and Tromba, A. J., ‘Degree theory on Banach manifolds’, inNonlinear Functional Analysis, Proceedings of Symposia in Pure Mathematics, Vol. XVIII, Part 1, Chicago, IL, 1968 (American Mathematical Society, Providence, RI, 1970), 86–94.CrossRefGoogle Scholar
Geba, K. and Granas, A., ‘Infinite dimensional cohomology theories’, J. Math. Pures Appl. (9) 52 (1973).Google Scholar
Goresky, M. and Hingston, N., ‘Loop products and closed geodesics’, Duke Math. J. 150(1) (2009), 117–209.CrossRefGoogle Scholar
Anna, G., Resolution of stratifolds and connection to Mather’s abstract pre-stratified spaces, PhD Heidelberg, 2002, http://archiv.ub.uni-heidelberg.de/volltextserver/3127/1/grinberg_diss.pdf.Google Scholar
Henderson, D. W., ‘Infinite-dimensional manifolds are open subsets of Hilbert space’, Bull. Amer. Math. Soc. (N.S.) 75(4) (1969), 759–762.CrossRefGoogle Scholar
Hirsch, M. W., Differential Topology, Graduate Texts in Mathematics, 33 (Springer, New York–Heidelberg, 1976).CrossRefGoogle Scholar
Jänich, K., ‘Vektorraumbündel und der Raum der Fredholm-Operatoren’, Math. Ann. 161 (1965).CrossRefGoogle Scholar
Koschorke, U., ‘Infinite dimensional K-theory and characteristic classes of Fredholm bundle maps’, PhD Thesis, Brandeis University, 1968.Google Scholar
Kreck, M., Differential Algebraic Topology: From Stratifolds to Exotic Spheres, Graduate Studies in Mathematics, 110 (American Mathematical Society, 2010).CrossRefGoogle Scholar
Kreck, M. and Singhof, W., ‘Homology and cohomology theories on manifolds’, Münster J. Math. 3 (2010), 1–9.Google Scholar
Kreck, M. and Tene, H., Extending functors on the category of manifolds and submersions, Manifold Atlas. http://www.map.mpim-bonn.mpg.de/Extending_functors_on_the_category_of_manifolds_and_submersions.Google Scholar
Kreck, M. and Tene, H., Orientation of Fredholm maps, Manifold Atlas. http://www.map.mpim-bonn.mpg.de/Orientation_of_Fredholm_maps_between_Hilbert_manifolds.Google Scholar
Kuiper, N. H., ‘The homotopy type of the unitary group of Hilbert space’, Topology 3(1) (1965).CrossRefGoogle Scholar
Lang, S., Fundamentals of Differential Geometry, Graduate Texts in Mathematics, 191 (Springer, New York, 1999).CrossRefGoogle Scholar
MacPherson, R., Equivariant Invariants and Linear Geometry, Geometric Combinatorics, IAS/Park City Mathematics Series, 13 (American Mathematical Society (AMS), Providence, RI, 2007, Princeton, NJ: Institute for Advanced Studies), 317–388.Google Scholar
Mather, J., ‘Notes on topological stability’, Bull. Amer. Math. Soc. (N.S.) 49(4) (2012), 475–506.CrossRefGoogle Scholar
Milnor, J. W., ‘On axiomatic homology theory’, Pacific J. Math. 12(1) (1962).CrossRefGoogle Scholar
Morava, J. J., ‘Algebraic topology of Fredholm maps’, Doctoral Thesis, Rice university, 1968, http://hdl.handle.net/1911/19013.Google Scholar
Mukherjea, K. K., ‘Cohomology theory for Banach manifolds’, J. Math. Mech. 19 (1969/1970), 731–744.Google Scholar
Palais, R. S., ‘Morse theory on Hilbert manifolds’, Topology 2 (1963), 299–340.CrossRefGoogle Scholar
Palais, R. S., ‘When proper maps are closed’, Proc. Amer. Math. Soc. 24 (1970), 835–836.Google Scholar
Pressley, A. and Segal, G., Loop Groups, Oxford Mathematical Monographs, Oxford Science Publications (The Clarendon Press, Oxford University Press, New York, 1986).Google Scholar
Quillen, D., ‘Elementary proofs of some results of cobordism theory using steenrod operations’, Adv. Math. 7(1) (1971), 29–56.CrossRefGoogle Scholar
Quillen, D., ‘Determinants of Cauchy–Riemann operators over a Riemann surface’, inFunctional Analysis and Its Applications 19 (Springer, New York, 1985), 31–34.Google Scholar
Smale, S., ‘An infinite dimensional version of Sard’s theorem’, Am. J. Math. 87(4) (1965).CrossRefGoogle Scholar
Tene, H., ‘Stratifolds and equivariant cohomology theories’, PhD Thesis, University of Bonn, 2010, http://hss.ulb.uni-bonn.de/2011/2391/2391.pdf.Google Scholar
Tene, H., Some geometric equivariant cohomology theories, http://arxiv.org/pdf/1210.7923v2.pdf.Google Scholar