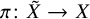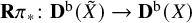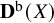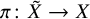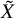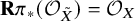1 Introduction
Operations of the Minimal Model Program often correspond to operations on the derived categories of coherent sheaves. The case of smooth varieties is understood relatively well. In particular, projective bundles, blow-ups, and standard flips correspond to semiorthogonal decompositions of derived categories, see [Reference Bondal and OrlovBO02] and references therein. Furthermore, the K-equivalence conjecture of Kawamata [Reference KawamataKaw02], building on ideas of Bondal and Orlov predicts that K-equivalent varieties should have equivalent derived categories. In particular, a crepant resolution of a singular variety is conjecturally unique up to derived equivalence. For a recent survey of various aspects of the interplay between birational geometry and derived categories for smooth projective varieties, see [Reference KawamataKaw18], and for conjectural relationship to rationality problems, see [Reference KuznetsovKuz16]. On the other hand, much less is known for singular varieties. In particular, the relationship between properties of the derived category of a singular variety and its resolution is still unclear. Of course this relationship should depend on the type of singularities of X. Recall that a variety X over a field of characteristic zero has rational singularities if the derived pushforward
${\mathbf {R}}\pi _*{\mathcal {O}}_{\tilde {X}}$
coincides with
${\mathcal {O}}_X$
for some (hence, every) resolution
$\pi \colon {\tilde {X}} \to X$
. One old major open question is the Bondal–Orlov localization conjecture:
Conjecture 1.1 [Reference Bondal and OrlovBO02, Section 5], [Reference EfimovEfi20, Conjecture 1.9]
Let
$\pi \colon {\tilde {X}} \to X$
be a resolution of rational singularities. Then the functor
$ {\mathbf {R}}\pi _*\colon {\mathbf {D}}^{\mathrm {b}}({\tilde {X}}) \to {\mathbf {D}}^{\mathrm {b}}(X)$
between bounded derived categories of coherent sheaves is a Verdier localization, that is the induced functor
$$\begin{align*}\overline{{\mathbf{R}}\pi_*}\colon {\mathbf{D}}^{\mathrm{b}}({\tilde{X}}) / \operatorname{{\mathrm{Ker}}}({\mathbf{R}}\pi_*) \to {\mathbf{D}}^{\mathrm{b}}(X)\end{align*}$$
is an equivalence.
It is convenient to split this statement into two parts:
-
(a) the induced functor
$\overline {{\mathbf {R}}\pi _*}\colon {\mathbf {D}}^{\mathrm {b}}({\tilde {X}}) / \operatorname {{\mathrm {Ker}}}({\mathbf {R}}\pi _*) \to {\mathbf {D}}^{\mathrm {b}}(X)$
is fully faithful; -
(b) the functor
${\mathbf {R}}\pi _*\colon {\mathbf {D}}^{\mathrm {b}}({\tilde {X}}) \to {\mathbf {D}}^{\mathrm {b}}(X)$
is essentially surjective.
Validity of Conjecture 1.1 does not depend on the choice of a resolution of X, at least in characteristic zero [Reference Pavic and ShinderPS21, Lemma 2.31]. Understanding this conjecture is essential for linking the Minimal Model Program to operations on derived categories, as well as for understanding derived categories of singular varieties. Indeed, a typical investigation of
${\mathbf {D}}^{\mathrm {b}}(X)$
proceeds by descending results from
${\mathbf {D}}^{\mathrm {b}}({\tilde {X}})$
to
${\mathbf {D}}^{\mathrm {b}}(X)$
, typically restricting to cases when the localization conjecture holds (see, e.g. [Reference Karmazyn, Kuznetsov and ShinderKKS22, Reference Kuznetsov and ShinderKS22a] for how this strategy can be implemented).
Recent progress on Conjecture 1.1 includes [Reference EfimovEfi20], [Reference Bondal, Kapranov and SchechtmanBKS18], and [Reference Pavic and ShinderPS21]. Notably, it holds for cones over projectively normal smooth Fano varieties [Reference EfimovEfi20] (as explained in [Reference Kuznetsov and ShinderKS22a, Example 5.4, Corollary 5.6]), all quotient singularities in characteristic zero [Reference Pavic and ShinderPS21, Theorem 2.30], and singularities admitting a resolution with one-dimensional fibers [Reference Bondal, Kapranov and SchechtmanBKS18, Theorem 2.14], however, in general, it remains wide open. Our main result is the weaker version of (b) which answers the question asked in [Reference Pavic and ShinderPS21, Introduction]. Let
${\mathrm {G}}_0(X) := {\mathrm {K}}_0({\mathbf {D}}^{\mathrm {b}}(X))$
be the Grothendieck group; it is isomorphic to the Grothendieck group of the abelian category of coherent sheaves on X. The group
${\mathrm {G}}_0(X)$
is covariantly functorial for proper morphisms, hence plays the role of a K-theoretic version of the Borel–Moore homology, similarly to Chow groups. By the “Homological Bondal–Orlov localization,” we mean the implications of Conjecture 1.1 for
${\mathrm {G}}_0(X)$
, as explained in [Reference Pavic and ShinderPS21, Section 4 of the Introduction]. We prove the following:
Theorem 1.2. Let
$\pi \colon {\tilde {X}} \to X$
be a proper morphism of algebraic varieties over a field
${\Bbbk }$
of characteristic zero with
$\tilde {X}$
smooth and satisfying
${\mathbf {R}}\pi _*({\mathcal {O}}_{\tilde {X}}) = {\mathcal {O}}_X$
. Then the image of
${\mathbf {R}}\pi _*\colon {\mathbf {D}}^{\mathrm {b}}({\tilde {X}}) \to {\mathbf {D}}^{\mathrm {b}}(X)$
generates
${\mathbf {D}}^{\mathrm {b}}(X)$
as a triangulated category. In particular, the induced homomorphism
$ {\mathbf {R}}\pi _*\colon {\mathrm {G}}_0({\tilde {X}}) \to {\mathrm {G}}_0(X) $
is surjective.
Here, we say that a set of objects
${\mathcal {S}} \subset {\mathbf {D}}^{\mathrm {b}}(X)$
generates
${\mathbf {D}}^{\mathrm {b}}(X)$
as a triangulated category if every object of
${\mathbf {D}}^{\mathrm {b}}(X)$
can be obtained from the objects of
${\mathcal {S}}$
by iterating cones and shifts. Importantly, taking direct summands is not required (this would make the statement much weaker, with no implications about the map on
${\mathrm {G}}_0$
).
We prove this by reducing to
${\Bbbk } = {\mathbb {C}}$
and using an argument from Hodge theory, going back to Steenbrink’s work on Hodge theory of singularities [Reference SteenbrinkSte83] (see Lemma 2.5 for this step). Theorem 1.2 applies, in particular, to resolutions of rational singularities. We note that this kind of surjectivity is specific to derived categories of coherent sheaves and
${\mathrm {G}}_0(X)$
; it is easy to find examples when it fails for other kinds of Borel–Moore homology theories, such as Chow groups or singular homology (see Examples 3.2 and 3.3).
Let us explain why Theorem 1.2, as well as the full Bondal–Orlov localization Conjecture 1.1, is a nontrivial and subtle statement. The key reason why the condition
${\mathbf {R}}\pi _*({\mathcal {O}}_{\tilde {X}}) = {\mathcal {O}}_X$
is relevant when studying derived categories of coherent sheaves is the projection formula: for every
${\mathcal {F}} \in {\mathbf {D}}^{\mathrm {b}}(X)$
$$\begin{align*}{\mathbf{R}}\pi_* {\mathbf{L}}\pi^*({\mathcal{F}}) \simeq {\mathcal{F}} \otimes {\mathbf{R}}\pi_*({\mathcal{O}}_{{\tilde{X}}}) = {\mathcal{F}}, \end{align*}$$
and this motivates at least part (b) of Conjecture 1.1. However, unless
${\mathcal {F}}$
is a perfect complex,
${\mathbf {L}}\pi ^*({\mathcal {F}})$
is a complex unbounded to the left, whereas the question is about existence of a bounded complex on
${\tilde {X}}$
. Thus, a certain truncation of
${\mathbf {L}}\pi ^*({\mathcal {F}})$
may be required, but a truncation does not immediately yield the complex we need, see [Reference KawamataKaw19, Lemma 7.4], where it is shown that
${\mathcal {F}}$
is a direct summand of the image of a truncation of
${\mathbf {L}}\pi ^*({\mathcal {F}})$
. In particular, we do not have a canonical lifting of a complex
${\mathcal {F}} \in {\mathbf {D}}^{\mathrm {b}}(X)$
or even its class
$[{\mathcal {F}}] \in {\mathrm {G}}_0(X)$
to
${\tilde {X}}$
.
Our approach is indirect: using standard K-theory arguments, it suffices to consider the structure sheaves
${\mathcal {O}}_Z \in {\mathbf {D}}^{\mathrm {b}}(X)$
of closed subvarieties
$Z \subset X$
. We construct a birational modification
$\sigma \colon {\tilde {X}}' \to {\tilde {X}}$
, such that the fibers of
$\pi \sigma $
, with their reduced scheme structure, have simple normal crossings, see Lemma 2.7. Hodge theory is used to prove that these fibers have no higher cohomology for the structure sheaf (see Proposition 2.4 and Lemma 2.5). We call the latter property of a morphism
${\mathcal {O}}$
-acyclicity, and we use it to show that
${\mathcal {O}}_Z$
lies in the image of
${\mathbf {R}}\pi _*$
eventually up to a small correction term, namely, that
${\mathcal {O}}_{Z}$
coincides with
${\mathbf {R}}\pi _*({\mathbf {R}}\sigma _*{\mathcal {O}}_{(\pi \sigma )^{-1}(Z)_{\mathrm {red}}})$
away from a proper subset of Z (see Lemma 2.8). Finally, we deduce Theorem 1.2 by induction on the dimension of Z (see Proposition 2.10).
From Theorem 1.2, we can deduce that part (b) of the Bondal–Orlov localization (essential surjectivity) already follows if we know part (a) (fully faithfulness):
Corollary 1.3. Under assumptions of Theorem 1.2, if
$\overline {{\mathbf {R}}\pi _*}\colon {\mathbf {D}}^{\mathrm {b}}({\tilde {X}})/\operatorname {{\mathrm {Ker}}}({\mathbf {R}}\pi _*) \to {\mathbf {D}}^{\mathrm {b}}(X)$
is full (i.e., surjective on
$\operatorname {{\mathrm {Hom}}}$
-spaces), then
$\overline {{\mathbf {R}}\pi _*}$
is essentially surjective. In particular, if
$\overline {{\mathbf {R}}\pi _*}$
is fully faithful, then it is a Verdier localization.
Thus, in the terminology of [Reference Kuznetsov and ShinderKS22a, Reference Kuznetsov and ShinderKS22b],
${\mathbf {R}}\pi _*$
is a Verdier localization if and only if it is a so-called categorical contraction, which is a priori a weaker statement meaning Verdier localization up to direct summands.
Notation and conventions
We work over a field
${\Bbbk }$
of characteristic zero. Unless stated otherwise, our varieties are assumed to be reduced and quasi-projective over
${\Bbbk }$
.
2
${\mathcal {O}}$
-acyclic morphisms and surjectivity of
${\mathbf {R}}\pi _*$
When working with derived categories and rational singularities, the following property is relevant.
Definition 2.1. Let
$\pi : {\tilde {X}} \to X$
be a surjective proper morphism with geometrically connected fibers. We say that
$\pi $
is
${\mathcal {O}}$
-acyclic at
$x \in X$
if
${\mathrm {H}}^{>0}(\pi ^{-1}(x)_{\mathrm {red}}, {\mathcal {O}}) = 0$
.
Here,
$x \in X$
is a scheme point and
$\pi ^{-1}(x)$
is a scheme of finite type over
${\Bbbk }(x)$
. Note that because we assume fibers to be geometrically connected, we have
$$ \begin{align} {\mathrm{H}}^{*}(\pi^{-1}(x)_{\mathrm{red}}, {\mathcal{O}}) = {\Bbbk}[0]. \end{align} $$
We say that
$\pi $
is
${\mathcal {O}}$
-acyclic if it is acyclic at each point
$x \in X$
, and we say that
$\pi $
is
${\mathcal {O}}$
-acyclic after a modification if there exists a proper morphism
$\sigma \colon {\tilde {X}}' \to {\tilde {X}}$
, such that
$\pi \sigma $
is
${\mathcal {O}}$
-acyclic.
The following lemma shows, in particular, that to check that
$\pi $
is
${\mathcal {O}}$
-acyclic, it suffices to consider fibers over closed points of X. Here,
$\pi $
is the morphism as in Definition 2.1.
Lemma 2.2.
$\pi $
is
${\mathcal {O}}$
-acyclic at
$x \in X$
if and only if it is acyclic at general closed points
$x' \in \overline {\{x\}}$
.
Proof. Let
$Z = \overline {\{x\}}$
and E be the reduced
$\pi $
-preimage of Z. The result follows from [Reference HartshorneHar77, Corollary 12.9] and the generic flatness of the restricted morphism
$\pi _Z\colon E \to Z$
.
In the case when
$\pi $
is flat and all fibers are reduced, being
${\mathcal {O}}$
-acyclic is equivalent to
${\mathbf {R}}\pi _*({\mathcal {O}}_{{\tilde {X}}}) = {\mathcal {O}}_X$
by base change. In general, the relation between these two properties is quite subtle.
Example 2.3. Let
$\pi \colon {\tilde {X}} \to X$
be a resolution of singularities. Then
$\pi $
can be
${\mathcal {O}}$
-acyclic, but
${\mathrm {R}}^{>0}\pi _*({\mathcal {O}}_{\tilde {X}}) \ne 0$
, because higher derived pushforwards involve thickenings in a nontrivial way.
-
(1) The map
$\pi $
can be chosen as a log resolution of a nonrational surface singularity whose exceptional locus E is a tree of rational curves. For instance, consider the Brieskorn singularity X given by the equation
$ x^2+y^3+z^7=0$
. The exceptional curve of its minimal resolution (the weighted blow-up with weights
$(3,2,1)$
) is the cuspidal cubic C given by
$x^2+y^3=0$
in
${\mathbf {P}}(3,2,1)$
, and so X does not have rational singularities by Artin’s rationality criterion since
${\mathrm {H}}^1(C, {\mathcal {O}})={\Bbbk }$
(see [Reference ArtinArt66, Proposition 1] or Example 2.6 below). On the other hand, by blowing-up the minimal resolution three times, we obtain a log resolution
$\pi \colon {\tilde {X}} \to X$
whose exceptional locus E is a tree of rational curves: its dual graph is
$D_4$
; the rational curve in the middle has self-intersection
$-1$
, and the other ones
$-2$
,
$-3$
, and
$-7$
. Note that
${\mathrm {H}}^{1}(E, {\mathcal {O}})=0$
, which means that
$\pi $
is
${\mathcal {O}}$
-acyclic. -
(2) Consider the affine cone X over a smooth projective variety
$Y \subset {\mathbb {P}}^N$
with
${\mathrm {H}}^{>0}(Y, {\mathcal {O}})=0$
but
${\mathrm {H}}^{>0}(Y, {\mathcal {O}}(1))\neq 0$
(see [Reference KollárKol13, Proposition 3.13]). For instance, one can take the surface suggested by Starr in [Reference ShinderShi]:
$Y \subset {\mathbb {P}}^2 \times {\mathbb {P}}^1$
is a divisor of bidegree
$(d,1)$
with
$d \ge 4$
. Then the blow-up of the vertex
$\pi \colon {\tilde {X}} \to X$
has reduced
${\mathcal {O}}$
-acyclic fibers (fibers consist of a point or of Y), but X is not a rational singularity.
In the opposite direction, we have the following:
Proposition 2.4. If
$\pi \colon {\tilde {X}} \to X$
is a proper morphism with
${\tilde {X}}$
smooth and satisfying
${\mathbf {R}}\pi _*({\mathcal {O}}_{\tilde {X}}) = {\mathcal {O}}_X$
, then
$\pi $
is
${\mathcal {O}}$
-acyclic after a modification.
This is a remarkable result, as we are essentially able to make a very naive base change statement for a morphism
$\pi $
which is not flat. Partial results of this kind can be obtained by the formal functions theorem (see Example 2.6), however, the formal functions theorem alone is not sufficient to control all cohomology groups of the fibers. We begin with the following particular case of Proposition 2.4 which we prove using complex algebraic geometry.
Lemma 2.5. Let
$\pi \colon {\tilde {X}} \to X$
be a proper morphism satisfying
${\mathbf {R}}\pi _*({\mathcal {O}}_{\tilde {X}}) = {\mathcal {O}}_X$
. Let
$x \in X$
be a closed point, and assume that
$E = \pi ^{-1}(x)_{\mathrm {red}}$
has simple normal crossings, then
$\pi $
is
${\mathcal {O}}$
-acyclic at x.
Proof. When
${\Bbbk } = {\mathbb {C}}$
, this result has been proved in [Reference Du BoisDB81, Proposition 3.1] for resolutions of cone singularities, and in [Reference SteenbrinkSte83, Proposition 3.7 and Section 3.6], [Reference IshiiIsh14, Propositions 8.1.11.(ii) and 8.1.12] or [Reference NamikawaNam01, Lemma 1.2] for resolutions of rational singularities. We give a self-contained proof for completeness. Extending the scalars, we can assume that
${\Bbbk }$
is an algebraically closed field. By the Lefschetz principle, we can further assume that
${\Bbbk } = {\mathbb {C}}$
and prove the result via Hodge theory. By the GAGA principle, the derived pushforward
${\mathbf {R}}\pi _*$
is the same when computed in the analytic or in the Zariski topology [Reference GrothendieckGro71, Expose XII Theorem 4.2]. Similarly,
${\mathrm {H}}^{*}(E, {\mathcal {O}})$
coincides when computed in the analytic or in the Zariski topology.
Let
$(V, x) \subseteq ({\mathbb {C}}^n, 0)$
be an affine neighborhood of x in X. The intersection of V with a ball of radius
$\epsilon $
centered at
$0$
, denoted
, is a Stein neighborhood of x in X. The preimage
$\pi ^{-1}(U)$
is an Euclidean neighborhood of E, and the inclusion
$j\colon E \to \pi ^{-1}(U)$
is a homotopy equivalence (see, e.g. [Reference DurfeeDur83, Proposition 1.6]). We consider the following diagram containing singular cohomology and analytic sheaf cohomology
Here, the horizontal maps are induced by sheaf inclusions
${\mathbb {C}} \subset {\mathcal {O}}$
and the vertical maps are restrictions. Since j is a homotopy equivalence, the left vertical map is an isomorphism. By the work of Deligne [Reference DeligneDel74], the cohomology groups of the simple normal crossing variety E carry a mixed Hodge structure, such that
$F^0 / F^1$
is canonically isomorphic to
${\mathrm {H}}^*(E, {\mathcal {O}})$
(see, e.g. [Reference SteenbrinkSte83, Section (1.5)]), hence, the bottom horizontal map is surjective. Thus, the right vertical map is surjective as well. Since
${\mathbf {R}}\pi _*({\mathcal {O}}_{\tilde {X}}) = {\mathcal {O}}_X$
and U is Stein, we have
${\mathrm {H}}^{>0}(\pi ^{-1}(U), {\mathcal {O}}) = 0$
, and this implies
${\mathrm {H}}^{>0}(E, {\mathcal {O}}) = 0$
.
We do not know if the conclusion of Lemma 2.5 holds for the scheme preimage itself, without taking reduced scheme structure. The assumption on the singularities of E can be weakened to the requirement that E has only Du Bois singularities, which grants the surjectivity of the morphism
${\mathrm {H}}^*(E, {\mathbb {C}}) \to {\mathrm {H}}^*(E, {\mathcal {O}})$
(see [Reference KovácsKov12, (1.4)] for details on Du Bois singularities). However, it is not clear whether the assumption on the singularities of E can be removed at all, at least when
$\pi $
is birational. This is true for resolution of rational singularities of dimension two or more, generally admitting a resolution with one-dimensional fibers by the following generalization of Artin’s rationality criterion (see [Reference ArtinArt66, Proposition 1]).
Example 2.6. Let
$\pi \colon {\tilde {X}} \to X$
be a proper morphism satisfying
${\mathbf {R}}\pi _*({\mathcal {O}}_{\tilde {X}}) = {\mathcal {O}}_X$
. Let
$x \in X$
be a schematic point and
$F \subset \pi ^{-1}(x)$
any closed subscheme; in particular, we can take
$F = \pi ^{-1}(x)$
or
$F = \pi ^{-1}(x)_{\mathrm {red}}$
. Suppose that
$d=\dim (\pi ^{-1}(x))>0$
. Then
${\mathrm {H}}^d(F, {\mathcal {O}})=0$
. Indeed, let
, where
$\mathfrak {m}_x$
is the maximal ideal of x. For
$k>0$
large enough, there exists an epimorphism
${\mathcal {O}}_{E_{k}} \to {\mathcal {O}}_{F}$
. For dimensional reasons, if
${\mathcal {K}}_k$
is the kernel of
${\mathcal {O}}_{E_{k}} \to {\mathcal {O}}_{F}$
, then
${\mathrm {H}}^{d+1}(E_{k},{\mathcal {K}}_k) = 0$
. Hence,
${\mathrm {H}}^d(F, {\mathcal {O}})=0$
as soon as
${\mathrm {H}}^d(E_{k}, {\mathcal {O}})=0$
. But the latter group vanishes by the formal functions theorem and
${\mathbf {R}}\pi _*({\mathcal {O}}_{\tilde {X}}) = {\mathcal {O}}_X$
:
$$\begin{align*}0=({\mathbf{R}}^{d}\pi_*({\mathcal{O}}_{\tilde{X}})_x)^{\wedge} = \lim_{\longleftarrow} {\mathrm{H}}^d(E_{k}, {\mathcal{O}}) \twoheadrightarrow {\mathrm{H}}^d(E_{k}, {\mathcal{O}}).\end{align*}$$
Surjectivity of the last map holds because all transition maps
${\mathrm {H}}^d(E_{k+1}, {\mathcal {O}}) \to {\mathrm {H}}^d(E_{k}, {\mathcal {O}})$
are surjective by the cohomology vanishing argument above.
The next result produces a desingularization of the fibers of a morphism. For completeness, we reproduce a proof due to Wlodarczyk.
Lemma 2.7 [Reference WlodarczykWlo16, Proposition 6.0.5]
Let
$\pi \colon {\tilde {X}} \to X$
be a proper morphism with
${\tilde {X}}$
smooth. Then there exists a morphism
$\sigma \colon {\tilde {X}}' \to {\tilde {X}}$
which is a composition of blow-ups along smooth centers, such that all fibers of
$\pi \sigma $
, with reduced scheme structure, are simple normal crossing varieties.
Proof. We will construct a sequence of (compositions of) smooth blow-ups
$$\begin{align*}{\tilde{X}}_n \overset{\sigma_n}\longrightarrow {\tilde{X}}_{n-1} \longrightarrow \dots \longrightarrow {\tilde{X}}_1 \overset{\sigma_1}\longrightarrow {\tilde{X}}_0 = {\tilde{X}} ,\end{align*}$$
such that for all
$k \le n$
, the morphism
$\pi \sigma _1 \cdots \sigma _k$
has simple normal crossing (snc) fibers over an open subset
$U_k \subset X$
with the complement
$X \setminus U_k$
of codimension at least
$k+1$
. Then we can take
${\tilde {X}}' = {\tilde {X}}_n$
and
$\sigma = \sigma _1 \cdots \sigma _n$
for
$n = \dim (X)$
. The variety
${\tilde {X}}_0 = {\tilde {X}}$
satisfies our assumptions because, by generic smoothness,
$\pi $
is smooth over a dense open subset of X. Assume that
${\tilde {X}}_{k-1}$
is constructed. Let
$Z = X \setminus U_{k-1}$
. By assumption, Z has codimension at least k. If the codimension of Z is strictly larger than k, we can set
${\tilde {X}}_k = {\tilde {X}}_{k-1}$
. Otherwise, let
$Z_1, \dots , Z_m$
be k-codimensional irreducible components of Z. Let
$\sigma _k\colon {\tilde {X}}_k \to {\tilde {X}}_{k-1}$
be a sequence of smooth blow-ups which provides a log-resolution of
$(\pi \sigma _1 \cdots \sigma _{k-1})^{-1}(Z_1 \cup \dots \cup Z_m)$
, that is, we require that
$\sigma _k$
is an isomorphism away from the preimages of
$Z_1, \dots , Z_m$
, and the preimage of every
$Z_i$
with respect to
$\pi \sigma _1 \cdots \sigma _k$
is an snc divisor. A simple argument using generic smoothness guarantees that there exists an open subset
$U_i \subseteq Z_i$
, such that for any
$x \in U_i$
, the fibers
$(\pi \sigma _1 \cdots \sigma _k)^{-1}(x)$
also have simple normal crossings (see, e.g. [Reference WlodarczykWlo16, Proposition 4.0.4]). Thus, the set of points
$x \in X$
, where
$(\pi \sigma _1 \cdots \sigma _k)^{-1}(x)$
is not an snc variety, is contained in a closed subset of codimension at least
$k+1$
.
Proof of Proposition 2.4
We take the modification
$\sigma $
from Lemma 2.7. Since
$\sigma $
is a birational modification of the smooth variety
${\tilde {X}}$
, we have
${\mathbf {R}} \sigma _*({\mathcal {O}}_{{\tilde {X}}'}) = {\mathcal {O}}_{{\tilde {X}}}$
, hence
${\mathbf {R}} (\pi \sigma )_*({\mathcal {O}}_{{\tilde {X}}'}) = {\mathcal {O}}_X$
. We need to check that
$\pi \sigma $
is
${\mathcal {O}}$
-acyclic. By Lemma 2.2, it suffices to prove the same for closed points
$x \in X$
. The result now follows from Lemma 2.5.
The following two lemmas are used in our inductive proof of Theorem 1.2.
Lemma 2.8. Let
$\pi \colon {\tilde {X}} \to X$
be
${\mathcal {O}}$
-acyclic at
$x \in X$
. Let
$Z \subset X$
be the closure of x and
$E \subset {\tilde {X}}$
be the reduced preimage of Z. Consider the complex
$$\begin{align*}{\mathcal{F}}_Z^\bullet := \operatorname{{\mathrm{Cone}}}({\mathcal{O}}_Z \to {\mathbf{R}}\pi_*({\mathcal{O}}_E)). \end{align*}$$
Then
${\mathcal {F}}_Z^\bullet $
is supported on a proper closed subset of Z.
Proof. Replacing
$\pi $
by the restricted morphism
$\pi _Z\colon E \to Z$
does not affect the definition of
${\mathcal {F}}_Z^\bullet $
. The fiber of
${\mathcal {F}}_Z^\bullet $
at the generic point
$x \in Z$
is isomorphic to
$$ \begin{align} \operatorname{{\mathrm{Cone}}}({\Bbbk}(x)[0] \to {\mathrm{H}}^*(E_x, {\mathcal{O}})), \end{align} $$
where
$E_x$
is the generic fiber of
$\pi _Z$
. By assumption,
$\pi _Z$
is
${\mathcal {O}}$
-acyclic at the generic point
$x \in Z$
, hence (1) implies that (2) vanishes. In particular,
${\mathcal {F}}_Z^\bullet $
vanishes at the generic point
$x \in Z$
. Therefore,
${\mathcal {F}}_Z^\bullet $
is supported on a proper closed subset of Z.
Lemma 2.9. Let
${\mathcal {D}}^m$
be the triangulated subcategory of
${\mathbf {D}}^{\mathrm {b}}(X)$
consisting of complexes acyclic away from a codimension m subset. Then
${\mathcal {D}}^m$
is generated by
${\mathcal {D}}^{m+1}$
and all
${\mathcal {O}}_Z$
for
$Z \subset X$
with Z integral,
$\operatorname {{\mathrm {codim}}}(Z) = m$
. In particular,
${\mathbf {D}}^{\mathrm {b}}(X)$
is generated by all structure sheaves
${\mathcal {O}}_Z$
.
Proof. This is the standard topological filtration argument in algebraic K-theory going back to Grothendieck (see, e.g. [Reference Calabrese and PirisiCP21, Lemma 1.7]). We recall the argument. Filtering complexes by their cohomology sheaves, it suffices to consider a coherent sheaf
${\mathcal {F}}$
set-theoretically supported on a reduced subscheme
$Z \subset X$
of codimension m. Each subquotient
${\mathcal {I}}_Z^n {\mathcal {F}} / {\mathcal {I}}_Z^{n+1} {\mathcal {F}}$
is a
${\mathcal {O}}_X / {\mathcal {I}}_Z$
–module, hence it is scheme-theoretically supported on Z so we can assume
${\mathcal {F}} = i_*({\mathcal {F}}_0)$
, where
$i\colon Z \to X$
is the inclusion, for a coherent sheaf
${\mathcal {F}}_0$
on Z. A simple argument using induction on the number of irreducible components of Z allows us to assume that Z is integral. In this case, since we assume X to be quasi-projective, there is a sufficiently ample line bundle
${\mathcal {O}}(H)$
and a morphism
$$\begin{align*}\phi\colon {\mathcal{O}}_Z^{\oplus n}(-H) \to {\mathcal{F}}_0 \end{align*}$$
which is an isomorphism over generic point of Z. In other words,
$\operatorname {{\mathrm {Cone}}}(\phi ) \in {\mathcal {D}}^{m+1}$
, and we can assume
${\mathcal {F}}_0$
is a line bundle
${\mathcal {O}}_Z(-H)$
on Z. The same argument using
$$\begin{align*}\operatorname{{\mathrm{Cone}}}({\mathcal{O}}_Z(-H) \to {\mathcal{O}}_Z) \simeq {\mathcal{O}}_{Z \cap H} \in {\mathcal{D}}^{m+1} \end{align*}$$
reduces the statement to the case
${\mathcal {F}}_0 = {\mathcal {O}}_Z$
, and we are done.
Proposition 2.10. If
$\pi $
is
${\mathcal {O}}$
-acyclic after a modification, then the image
${\mathbf {R}}\pi _*({\mathbf {D}}^{\mathrm {b}}({\tilde {X}}))$
generates
${\mathbf {D}}^{\mathrm {b}}(X)$
as a triangulated category.
Proof. By definition, there exists a birational morphism
$\sigma \colon {\tilde {X}}' \to {\tilde {X}}$
of smooth varieties, such that
$\pi \sigma $
is
${\mathcal {O}}$
-acyclic. Since
${\mathbf {R}}\pi _*({\mathbf {D}}^{\mathrm {b}}({\tilde {X}}))$
contains
${\mathbf {R}}(\pi \sigma )_*({\mathbf {D}}^{\mathrm {b}}({\tilde {X}}))$
, it suffices to show that
${\mathbf {R}}(\pi \sigma )_*({\mathbf {D}}^{\mathrm {b}}({\tilde {X}}))$
generates
${\mathbf {D}}^{\mathrm {b}}(X)$
as a triangulated category.
Let
${\mathcal {T}}$
be the triangulated subcategory of
${\mathbf {D}}^{\mathrm {b}}(X)$
generated by
${\mathbf {R}}(\pi \sigma )_*({\mathbf {D}}^{\mathrm {b}}({\tilde {X}}))$
. We need to show that
${\mathcal {T}} = {\mathbf {D}}^{\mathrm {b}}(X)$
. Let
${\mathcal {D}}^m$
be the subcategory of
${\mathbf {D}}^{\mathrm {b}}(X)$
consisting of complexes acyclic away from a codimension m subset. We check by the descending induction on m that
${\mathcal {D}}^m \subset {\mathcal {T}}$
for all
$0 \le m \le \dim (X) + 1$
; this proves the result because
${\mathcal {D}}^0 = {\mathbf {D}}^{\mathrm {b}}(X)$
. For the induction, base
${\mathcal {D}}^{\dim (X)+1}$
consists of the zero-complex, so the statement holds. Assume
${\mathcal {D}}^{m+1} \subset {\mathcal {T}}$
, for some
$m \ge 0$
. To show that
${\mathcal {D}}^{m} \subset {\mathcal {T}}$
, by Lemma 2.9, it suffices to check that for all integral subschemes
$Z \subset X$
of codimension m, we have
${\mathcal {O}}_Z \in {\mathcal {T}}$
. Let
$x \in Z$
be the generic point. By Lemma 2.8, applied to
$\pi \sigma $
,
${\mathcal {F}}_Z^\bullet $
is a complex supported on a proper closed subset of Z and the statement follows by the induction hypothesis.
Proof of Theorem 1.2
By Proposition 2.4,
$\pi $
is
${\mathcal {O}}$
-acyclic after a modification, hence, by Proposition 2.10, the image of
${\mathbf {R}}\pi _*$
generates
${\mathbf {D}}^{\mathrm {b}}(X)$
.
Proof of Corollary 1.3
Let
${\mathcal {T}} \subseteq {\mathbf {D}}^{\mathrm {b}}(X)$
be the image of
$\overline {{\mathbf {R}}\pi _*}$
. Then
${\mathcal {T}}$
is closed under shifts, and since
$\overline {{\mathbf {R}}\pi _*}$
is assumed to be full,
${\mathcal {T}}$
is also closed under taking cones of morphisms. Thus,
${\mathcal {T}}$
is a triangulated subcategory of
${\mathbf {D}}^{\mathrm {b}}(X)$
. On the other hand, by Theorem 1.2,
${\mathcal {T}}$
generates
${\mathbf {D}}^{\mathrm {b}}(X)$
as a triangulated category. Since
${\mathcal {T}}$
is already closed under taking shifts and cones, we obtain
${\mathcal {T}} = {\mathbf {D}}^{\mathrm {b}}(X)$
.
3 Examples and counterexamples
Both Bondal–Orlov Conjecture 1.1 and Theorem 1.2 fail when X does not have rational singularities.
Example 3.1. If
${\Bbbk }$
is a nonclosed field,
$C \subset {\mathbb {P}}^2$
is a smooth cubic curve without rational points,
$X \subset {\mathbf {A}}^3$
is a cone over C, and
${\tilde {X}}$
is the blow-up of the vertex of the cone X. The singularity is not rational, and
${\mathbf {R}}\pi _*\colon {\mathrm {G}}_0({\tilde {X}}) \to {\mathrm {G}}_0(X)$
is not surjective because the image does not contain
$[{\mathcal {O}}_P]$
, essentially because the Euler characteristic of every object
${\mathcal {E}} \in {\mathbf {D}}^{\mathrm {b}}(C)$
is divisible by
$3$
, hence never equals one.
In Theorem 1.2, we cannot replace the Grothendieck group
$G_0(X)$
with either integral Chow groups or Borel–Moore homology. We explain this in detail.
For Chow groups with rational coefficients, the induced map
$\pi _* \colon \operatorname {{\mathrm {CH}}}_*(\tilde {X}, {\mathbb {Q}}) \to \operatorname {{\mathrm {CH}}}_*(X, {\mathbb {Q}})$
is always surjective for a proper morphism
$\pi \colon {\tilde {X}} \to X$
, since any closed subset
$Z \subseteq X$
is dominated by a closed subset
$\tilde {Z} \subseteq \tilde {X}$
, such that the restriction
$\pi |_{\tilde {Z}} \colon \tilde {Z} \to Z$
is generically finite. However, integrally, this is not always the case.
Example 3.2. If
${\Bbbk }$
is a nonclosed field,
$X \subset {\mathbf {A}}^3$
is a cone over a conic C without rational points, and
${\tilde {X}}$
is the blow-up of the vertex of the cone X, then
$\pi _*\colon \operatorname {{\mathrm {CH}}}_0({\tilde {X}})=\operatorname {{\mathrm {CH}}}_0(C) \to \operatorname {{\mathrm {CH}}}_0(X)={\mathbb {Z}}$
is not surjective, since the pushforward of any 0-cycle in C has even degree.
Examples analogous to Examples 3.1 and 3.2 can be constructed over
${\Bbbk } = {\mathbb {C}}$
by spreading out. We now consider pushforwards for Borel–Moore homology for complex varieties, which for proper varieties coincides with the usual homology.
Example 3.3. Let X be a projective complex threefold with only isolated nodal (thus rational) singularities and
$\pi \colon \tilde {X} \to X$
be the blow-up of the nodes
$\Sigma $
of X with exceptional divisor
$E_p \simeq {\mathbf {P}}^1 \times {\mathbf {P}}^1$
for
$p \in \Sigma $
. The pushforward
${\mathrm {H}}_3({\tilde {X}}, {\mathbb {Q}}) \to {\mathrm {H}}_3(X, {\mathbb {Q}})$
may not be surjective.
To explain this, we need to introduce some notation. Let
$\delta (X) := \operatorname {{\mathrm {rk}}}(\operatorname {{\mathrm {Cl}}}(X)/\operatorname {{\mathrm {Pic}}}(X))$
be the defect of X. We have
$0 \le \delta (X) \le |\Sigma |$
(see, e.g. [Reference Kalck, Pavic and ShinderKPS21, Corollary 3.8]). Furthermore, if X is a nodal hypersurface in
${\mathbb {P}}^4$
of degree
$d \ge 3$
, or a nodal double cover of
${\mathbb {P}}^3$
branched in a surface of degree
$d \ge 4$
, then
$\delta (X) < |\Sigma |$
(see [Reference Kalck, Pavic and ShinderKPS21, Example 3.13]). The defect
$\delta (X)$
can be computed from the resolution
${\tilde {X}}$
via
$$\begin{align*}|\Sigma| - \delta(X) = \operatorname{{\mathrm{rk}}} \operatorname{{\mathrm{Coker}}}\left(\operatorname{{\mathrm{Pic}}}({\tilde{X}}) \to \bigoplus_{p \in \Sigma} \operatorname{{\mathrm{Pic}}}(E_p)\right) = \operatorname{{\mathrm{rk}}} \operatorname{{\mathrm{Coker}}}\left(H^2({\tilde{X}}) \to \bigoplus_{p \in \Sigma} {\mathrm{H}}^2(E_p)\right), \end{align*}$$
where cohomology are taken with integral or rational coefficients. Using duality, we can also write
$$\begin{align*}|\Sigma| - \delta(X) = \operatorname{{\mathrm{rk}}} \operatorname{{\mathrm{Ker}}}\left(\bigoplus_{p \in \Sigma} {\mathrm{H}}_2(E_p) \to {\mathrm{H}}_2({\tilde{X}})\right). \end{align*}$$
The Mayer–Vietoris exact sequence for the mapping cylinder of
$\pi $
reads
$$\begin{align*}{\mathrm{H}}_3(\tilde{X}) \xrightarrow{\pi_*} {\mathrm{H}}_3(X) \to \bigoplus_{p \in \Sigma} {\mathrm{H}}_2(E_p) \to {\mathrm{H}}_2(\tilde{X}), \end{align*}$$
thus,
$\pi _* \colon {\mathrm {H}}_3(\tilde {X}) \to {\mathrm {H}}_3(X)$
is not surjective provided
$\delta (X) < |\Sigma |$
.
We may restrict to the pure part of the homology
${\mathrm {H}}^{\mathrm {BM}}_{\mathrm {pure}, i}(X, {\mathbb {Q}})$
, that is, the lower piece of the weight filtration of Deligne’s mixed Hodge structure on
${\mathrm {H}}^{\mathrm {BM}}_{i}(X, {\mathbb {Q}})$
. If
$\pi \colon \tilde {X} \to X$
is a resolution of singularities of a proper normal complex variety X, then
$\pi _* \colon {\mathrm {H}}_{i}(\tilde {X}, {\mathbb {Q}}) \to {\mathrm {H}}_{\mathrm {pure}, i}(X, {\mathbb {Q}})$
is surjective, independently of the singularities of X (see [Reference Peters and SteenbrinkPS08, Theorem 5.41]).
Acknowledgements
We thank Agnieszka Bodzenta-Skibińska, Paolo Cascini, Wahei Hara, Sándor Kovács, Alexander Kuznetsov, Mircea Musta
ă, Nebojsa Pavic, Pavel Sechin, and Michael Wemyss for discussions and e-mail correspondence. We also thank the anonymous referee for the helpful comments. M.M. was supported by the Institute of Science and Technology Austria. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 101034413. E.S. was partially supported by the EPSRC grant EP/T019379/1 “Derived categories and algebraic K-theory of singularities”, and by the ERC Synergy grant “Modern Aspects of Geometry: Categories, Cycles and Cohomology of Hyperkähler Varieties.”
Competing interest
The authors have no competing interest to declare.
Open access
