Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-09T13:35:15.637Z Has data issue: false hasContentIssue false
  • English
  • Français

WHEN DOES THE BOMBIERI–VINOGRADOV THEOREM HOLD FOR A GIVEN MULTIPLICATIVE FUNCTION?

Part of: Multiplicative number theory

Published online by Cambridge University Press:  24 August 2018

ANDREW GRANVILLE  and
XUANCHENG SHAO
ANDREW GRANVILLE
Affiliation:
Département de mathématiques et de statistique, Université de Montréal, CP 6128 succ. Centre-Ville, Montréal, QC H3C 3J7, Canada Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK; andrew@dms.umontreal.ca
XUANCHENG SHAO
Affiliation:
Department of Mathematics, University of Kentucky, 715 Patterson Office Tower, Lexington, KY 40502, USA; Xuancheng.Shao@uky.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 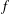$f$ and 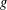$g$ be 1-bounded multiplicative functions for which 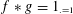$f\ast g=1_{.=1}$. The Bombieri–Vinogradov theorem holds for both 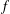$f$ and 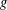$g$ if and only if the Siegel–Walfisz criterion holds for both 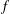$f$ and 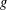$g$, and the Bombieri–Vinogradov theorem holds for 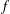$f$ restricted to the primes.

MSC classification

Primary: 11N56: Rate of growth of arithmetic functions
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e15
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2018

References

Bombieri, E., Friedlander, J. B. and Iwaniec, H., ‘Primes in arithmetic progressions to large moduli’, Acta Math. 156 (1986), 203–251.Google Scholar
Drappeau, S., Granville, A. and Shao, X., ‘Smooth-supported multiplicative functions in arithmetic progressions beyond the x 1/2 -barriers’, Mathematika 63(3) (2017), 895–918.Google Scholar
Friedlander, J. B. and Iwaniec, H., Opera de Cribro, AMS Colloquium Publications , vol. 57. (American Mathematical Society, Providence, RI, 2010).Google Scholar
Granville, A. and Shao, X., Bombieri–Vinogradov for multiplicative functions, and beyond the $x^{1/2}$ -barrier, Preprint.Google Scholar
Harper, A., Bombieri–Vinogradov and Barban–Davenport–Halberstam type theorems for smooth numbers, Preprint.Google Scholar
Koukoulopoulos, D., ‘On multiplicative functions which are small on average’, Geom. Funct. Anal. 23 (2013), 1569–1630.Google Scholar