Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-18T04:30:34.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Poisson superposition processes

Part of: Stochastic processes

Published online by Cambridge University Press:  30 March 2016

Harry Crane  and
Peter Mccullagh
Harry Crane*
Affiliation:
Rutgers University
Peter Mccullagh*
Affiliation:
University of Chicago
*
∗Postal address: Department of Statistics, Rutgers University, 110 Frelinghuysen Road, Piscataway, NJ 08854, USA. Email address: hcrane@stat.rutgers.edu
∗∗Postal address: Department of Statistics, University of Chicago, Eckhart Hall, 5734 S. University Avenue, Chicago, IL 60637, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Superposition is a mapping on point configurations that sends the n-tuple 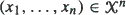into the n-point configuration , counted with multiplicity. It is an additive set operation such that the superposition of a k-point configuration in 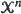is a kn-point configuration in 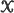. A Poisson superposition process is the superposition in 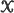of a Poisson process in the space of finite-length 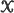-valued sequences. From properties of Poisson processes as well as some algebraic properties of formal power series, we obtain an explicit expression for the Janossy measure of Poisson superposition processes, and we study their law under domain restriction. Examples of well-known Poisson superposition processes include compound Poisson, negative binomial, and permanental (boson) processes.

Keywords

Poisson point processpermanental processcompound Poisson processnegative binomial distributionPoisson superposition

MSC classification

Primary: 60G55: Point processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 52 , Issue 4 , December 2015 , pp. 1013 - 1027
Copyright
Copyright © Applied Probability Trust 2015 

References

Arratia, R., Barbour, A. D. and Tavare, S. (1992). Poisson process approximations for the Ewens sampling formula. Ann. Appl. Prob. 2, 519–535.Google Scholar
Barndorff-Nielsen, O. and Yeo, G. F. (1969). Negative binomial processes. J. Appl. Prob. 6, 633–647.Google Scholar
Cox, D. R. and Isham, V. (1980). Point Processes. Chapman & Hall, London.Google Scholar
Crane, H. (2013a). Permanental partition models and Markovian Gibbs structures. J. Statist. Phys. 153, 698–726.Google Scholar
Crane, H. (2013b). Some algebraic identities for the a-permanent. Linear Algebra Appl. 439, 3445–3459.Google Scholar
Donnelly, P. and Grimmett, G. (1993). On the asymptotic distribution of large prime factors. J. London Math. Soc. (2) 47, 395–404.Google Scholar
Ewens, W. J. (1972). The sampling theory of selectively neutral alleles. Theoret. Pop. Biol. 3, 87–112, 240, 376.Google Scholar
Fisher, R. A., Corbet, A. S. and Williams, C. B. (1943). The relation between the number of species and the number of individuals in a random sample of an animal population. J. Animal Ecol. , 12, 42–58.Google Scholar
Hough, J. B., Krishnapur, M., Peres, Y. and ViráG, B. (2006). Determinantal processes and independence. Prob. Surveys 3, 206–229.CrossRefGoogle Scholar
Kingman, J. F. C. (1978). Random partitions in population genetics. Proc. R. Soc. London A 361, 1–20.Google Scholar
Kingman, J. F. C. (1978). The representation of partition structures. J. London Math. Soc. (2) 18, 374–380.Google Scholar
Kingman, J. F. C. (1993). Poisson Processes. Oxford University Press.Google Scholar
Macchi, O. (1975). The coincidence approach to stochastic point processes. Adv. Appl. Prob. 7, 83–122.Google Scholar
Mccullagh, P. (1987). Tensor Methods in Statistics. Chapman & Hall, London.Google Scholar
Mccullagh, P. and M⊘ller, J. (2006). The permanental process. Adv. Appl. Prob. 38, 873–888.Google Scholar
Pitman, J. (2006). Combinatorial Stochastic Processes (Lecture Notes Math. 1875). Springer, Berlin.Google Scholar
Rubak, E., M⊘ller, J. and Mccullagh, P. (2010). Statistical inference for a class of multivariate negative binomial distributions. Res. Rep. R-2010–10, Department of Mathematical Sciences, Aalborg University.Google Scholar
Streitberg, B. (1990). Lancaster interactions revisited. Ann. Statist. 18, 1878–1885.Google Scholar
Valiant, L. G. (1979). The complexity of computing the permanent. Theoret. Comput. Sci. 8, 189–201.Google Scholar
Vere-Jones, D. (1988). A generalization of permanents and determinants. Linear Algebra Appl. 111, 119–124.Google Scholar
Vere-Jones, D. (1997). Alpha-permanents and their applications to mulivariate gamma, negative binomial and ordinary binomial distributions. New Zealand J. Math. 26, 125–149.Google Scholar
Wilf, H. S. (2006). Generating functionology, 3rd edn. A K Peters, Wellesey, MA.Google Scholar