Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-05-12T06:48:02.445Z Has data issue: false hasContentIssue false
  • English
  • Français

Recurrence and transience of a Markov chain on 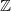$\mathbb Z$+ and evaluation of prior distributions for a Poisson mean

Part of: Decision theory Markov processes

Published online by Cambridge University Press:  25 April 2024

James P. Hobert  and
Kshitij Khare
James P. Hobert*
Affiliation:
University of Florida
Kshitij Khare*
Affiliation:
University of Florida
*
*Postal address: Department of Statistics, 103 Griffin Floyd Hall, University of Florida, Gainesville, FL 32611, USA.
*Postal address: Department of Statistics, 103 Griffin Floyd Hall, University of Florida, Gainesville, FL 32611, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Eaton (1992) considered a general parametric statistical model paired with an improper prior distribution for the parameter and proved that if a certain Markov chain, constructed using the model and the prior, is recurrent, then the improper prior is strongly admissible, which (roughly speaking) means that the generalized Bayes estimators derived from the corresponding posterior distribution are admissible. Hobert and Robert (1999) proved that Eaton’s Markov chain is recurrent if and only if its so-called conjugate Markov chain is recurrent. The focus of this paper is a family of Markov chains that contains all of the conjugate chains that arise in the context of a Poisson model paired with an arbitrary improper prior for the mean parameter. Sufficient conditions for recurrence and transience are developed and these are used to establish new results concerning the strong admissibility of non-conjugate improper priors for the Poisson mean.

Keywords

Admissibilityelectrical networknull recurrencePoisson distributionreversibilityweighted random walk

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 62C15: Admissibility
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Billingsley, P. (1995). Probability and Measure, 3rd edn. John Wiley, New York.Google Scholar
Brown, L. D. (1971). Admissible estimators, recurrent diffusions, and insoluble boundary value problems. Ann. Math. Statist. 42, 855–904.CrossRefGoogle Scholar
Doyle, P. J. and Snell, J. L. (1984). Random Walks and Electric Networks. Mathematical Association of America, Washington, DC.CrossRefGoogle Scholar
Eaton, M. L. (1992). A statistical diptych: Admissible inferences-recurrence of symmetric Markov chains. Ann. Statist. 20, 1147–1179.CrossRefGoogle Scholar
Eaton, M. L. (2004). Evaluating improper priors and the recurrence of symmetric Markov chains: An overview. In A Festschrift to Honor Herman Rubin, ed. A. Dasgupta (IMS Lect. Notes Ser. 45). Institute of Mathematical Statistics, Beachwood, OH.Google Scholar
Eaton, M. L., Hobert, J. P. and Jones, G. L. (2007). On perturbations of strongly admissible prior distributions. Ann. Inst. H. Poincaré Prob. Statist. 43, 633–653.CrossRefGoogle Scholar
Hobert, J. P. and Robert, C. P. (1999). Eaton’s Markov chain, its conjugate partner and $\mathcal{P}$ -admissibility. Ann. Statist. 27, 361–373.CrossRefGoogle Scholar
Hobert, J. P. and Schweinsberg, J. (2002). Conditions for recurrence and transience of a Markov chain on ${\mathbb Z}^+$ and estimation of a geometric success probability. Ann. Statist. 30, 1214–1223.CrossRefGoogle Scholar
Johnstone, I. (1984). Admissibility, difference equations, and recurrence in estimating a Poisson mean. Ann. Statist. 12, 1173–1198.CrossRefGoogle Scholar
Lai, W.-L. (1996). Admissibility and the recurrence of Markov chains with applications. Tech. Rep. No. 612, School of Statistics, University of Minnesota.Google Scholar
Lyons, T. (1983). A simple criterion for transience of a reversible Markov chain. Ann. Prob. 11, 393–402.CrossRefGoogle Scholar
McGuinness, S. (1991). Recurrent networks and a theorem of Nash–Williams. J. Theoret. Prob. 4, 87–100.CrossRefGoogle Scholar
Peres, Y. (1999). Probability on trees: An introductory climb. In Lectures on Probability Theory and Statistics, ed. Bernard, P. (Lect. Notes Math. 1717). Springer, New York, pp. 193-280.Google Scholar
Segura, J. (2023). Simple bounds with best possible accuracy for ratios of modified Bessel functions. J. Math. Anal. Appl. 526, 127211.CrossRefGoogle Scholar
Wendel, J. G. (1948). Note on the gamma function. Amer. Math. Monthly 55, 563–564.CrossRefGoogle Scholar