Article contents
A Stochastic Maximin Fixed-Point Equation Related to Game Tree Evaluation
Published online by Cambridge University Press: 14 July 2016
Abstract
After suitable normalization the asymptotic root value W of a minimax game tree of order b ≥ 2 with independent and identically distributed input values having a continuous, strictly increasing distribution function on a subinterval of R appears to be a particular solution of the stochastic maximin fixed-point equation W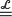 ξ max1≤i≤bmin1≤j≤bWi,j, where Wi,j are independent copies of W and
ξ max1≤i≤bmin1≤j≤bWi,j, where Wi,j are independent copies of W and 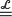 denotes equality in law. Moreover, ξ= g'(α) > 1, where g(x) := (1 − (1 − x)b)b and α denotes the unique fixed point of g in (0, 1). This equation, which takes the form F(t) = g(F(t/ξ)) in terms of the distribution function F of W, is studied in the present paper for a reasonably extended class of functions g so as to encompass more general stochastic maximin equations as well. A complete description of the set of solutions F is provided followed by a discussion of additional properties such as continuity, differentiability, or existence of moments. Based on these results, it is further shown that the particular solution mentioned above stands out among all other ones in that its distribution function is the restriction of an entire function to the real line. This extends recent work of Ali Khan, Devroye and Neininger (2005). A connection with another class of stochastic fixed-point equations for weighted minima and maxima is also discussed.
denotes equality in law. Moreover, ξ= g'(α) > 1, where g(x) := (1 − (1 − x)b)b and α denotes the unique fixed point of g in (0, 1). This equation, which takes the form F(t) = g(F(t/ξ)) in terms of the distribution function F of W, is studied in the present paper for a reasonably extended class of functions g so as to encompass more general stochastic maximin equations as well. A complete description of the set of solutions F is provided followed by a discussion of additional properties such as continuity, differentiability, or existence of moments. Based on these results, it is further shown that the particular solution mentioned above stands out among all other ones in that its distribution function is the restriction of an entire function to the real line. This extends recent work of Ali Khan, Devroye and Neininger (2005). A connection with another class of stochastic fixed-point equations for weighted minima and maxima is also discussed.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Applied Probability Trust 2007
References
- 1
- Cited by




