Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T09:37:36.579Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent dynamics of sinusoidal oscillatory flow over a wavy bottom

Published online by Cambridge University Press:  02 November 2018

Asim Önder Open the ORCID record for Asim Önder [Opens in a new window]  and
Jing Yuan
Asim Önder*
Affiliation:
Department of Civil and Environmental Engineering, National University of Singapore, Singapore 117576, Singapore
Jing Yuan
Affiliation:
Department of Civil and Environmental Engineering, National University of Singapore, Singapore 117576, Singapore
*
†Email address for correspondence: asim.onder@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A direct numerical simulation study is conducted to investigate sinusoidal oscillatory flow over a two-dimensional wavy wall. The height and wavelength of the bottom profile, and the period and amplitude of the free-stream oscillation, are selected to mimic a wave-driven boundary layer over vortex ripples on a sandy seabed. Two cases with different Reynolds numbers 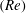$(Re)$ are considered, and the higher-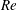$Re$ case achieves a fully developed turbulent state with a wide separation between the energy-containing and dissipative scales. The oscillatory flow is characterized by coherent columnar vortices, which are the main transport agents of turbulent kinetic energy and enstrophy. Two classes of coherent vortices are observed: (i) a primary vortex formed at the lee side of the ripple by flow separation at the crest; (ii) a secondary vortex formed beneath the primary vortex by vortex-induced separation. When the free-stream velocity weakens, these vortices form a counter-rotating vortex dipole and eject themselves over the crest with their mutual induction. Turbulence production peaks twice in a half-cycle; during the formation of the primary vortex and during the ejection of the vortex dipole. The intensity of the former peak remains low in the lower-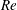$Re$ case, as the vortex dipole follows a higher altitude trajectory limiting its interactions with the bottom, and leaving minimal residual turbulence around the ripples for the subsequent half-cycle. Flow snapshots and spectral analysis reveal two dominant three-dimensional features: (i) an energetic vortex mode with a preferred spanwise wavelength close to the ripple wavelength; (ii) streamwise vortical structures in near-wall regions with a relatively shorter spanwise spacing influenced by viscous effects. The vortex mode becomes strong when the cores of the vortices are strained to an elliptical form while moving towards the crest. Following the detachment of the vortices from the ripple, the vortex mode in the higher-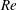$Re$ case breaks down the spanwise coherence of the columnar vortices and decomposes them into intermittent patches of turbulent vortex clusters. The distribution of wall shear stress over the ripple is also analysed in detail. The peak values are observed near the ripple crest around the ejection of the vortex dipole and the maximum free-stream velocity. In the former, both the vortex mode and streamwise vortices have strong footprints on the wall, yielding a bimodal wall-shear-stress spectrum with two distinctive peaks. In the second high-stress regime, decaying coherent vortices impose strong inhomogeneity on the wall shear stress as their wall-attached parts sweep the ripples. These spanwise variations in the wall shear provide insights into the instability of two-dimensional sand ripples.

JFM classification

Geophysical and Geological Flows: Coastal engineering Wakes/Jets: Separated flows Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 264 - 314
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bagnold, R. A. & Taylor, G. 1946 Motion of waves in shallow water. Interaction between waves and sand bottoms. Proc. R. Soc. Lond. A 187 (1008), 1–18.Google Scholar
Batchelor, G. K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1949 The nature of turbulent motion at large wave-numbers. Proc. R. Soc. Lond. A 199 (1057), 238–255.Google Scholar
Blondeaux, P., Scandura, P. & Vittori, G. 2004 Coherent structures in an oscillatory separated flow: numerical experiments. J. Fluid Mech. 518, 215–229.Google Scholar
Blondeaux, P. & Vittori, G. 1991 Vorticity dynamics in an oscillatory flow over a rippled bed. J. Fluid Mech. 226, 257–289.Google Scholar
Blondeaux, P. & Vittori, G. 1999 Boundary layer and sediment dynamics under sea waves. Adv. Coastal Ocean Engng 4, 133–190.Google Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods. Courier Corporation.Google Scholar
Buxton, O. R. H., Breda, M. & Chen, X. 2017 Invariants of the velocity-gradient tensor in a spatially developing inhomogeneous turbulent flow. J. Fluid Mech. 817, 1–20.Google Scholar
Canals, M. & Pawlak, G. 2011 Three-dimensional vortex dynamics in oscillatory flow separation. J. Fluid Mech. 674, 408–432.Google Scholar
Cantwell, C. D. et al. 2015 Nektar++: an open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219.Google Scholar
Corrsin, S.1958 Local isotropy in turbulent shear flow. Tech. Rep. NACA-RM-58B11. National Advisory Committee for Aeronautics.Google Scholar
Darwin, G. H. 1883 On the formation of ripple-mark in sand. Proc. R. Soc. Lond. A 36 (228–231), 18–43.Google Scholar
Del Álamo, J. C., Jimenez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409 (1), 69–98.Google Scholar
Doligalski, T. L., Smith, C. R. & Walker, J. D. A. 1994 Vortex interactions with walls. Annu. Rev. Fluid Mech. 26 (1), 573–616.Google Scholar
Earnshaw, H. C. & Greated, C. A. 1998 Dynamics of ripple bed vortices. Exp. Fluids 25 (3), 265–275.Google Scholar
Fredsøe, J., Andersen, K. H. & Sumer, B. M. 1999 Wave plus current over a ripple-covered bed. Coast. Engng 38 (4), 177–221.Google Scholar
Ghodke, C. D. & Apte, S. V. 2016 DNS study of particle-bed–turbulence interactions in an oscillatory wall-bounded flow. J. Fluid Mech. 792, 232–251.Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2014 Evolution of the velocity-gradient tensor in a spatially developing turbulent flow. J. Fluid Mech. 756, 252–292.Google Scholar
Grigoriadis, D. G. E., Dimas, A. A. & Balaras, E. 2012 Large-eddy simulation of wave turbulent boundary layer over rippled bed. Coast. Engng 60, 174–189.Google Scholar
Gschwind, P., Regele, A. & Kottke, V. 1995 Sinusoidal wavy channels with Taylor–Goertler vortices. Exp. Therm. Fluid Sci. 11 (3), 270–275.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Günther, A. & Von Rohr, P. R. 2003 Large-scale structures in a developed flow over a wavy wall. J. Fluid Mech. 478, 257–285.Google Scholar
Hara, T. & Mei, C. C. 1990 Centrifugal instability of an oscillatory flow over periodic ripples. J. Fluid Mech. 217, 1–32.Google Scholar
Hare, J., Hay, A. E., Zedel, L. & Cheel, R. 2014 Observations of the space-time structure of flow, turbulence, and stress over orbital-scale ripples. J. Geophys. Res. 119 (3), 1876–1898.Google Scholar
Honji, H., Kaneko, A. & Matsunaga, N. 1980 Flows above oscillatory ripples. Sedimentology 27 (2), 225–229.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.Google Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Jensen, B. L., Sumer, B. M. & Fredsoe, J. 1989 Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech. 206, 265–297.Google Scholar
Jespersen, T. S., Thomassen, J. Q., Andersen, A. & Bohr, T. 2004 Vortex dynamics around a solid ripple in an oscillatory flow. Eur. Phys. J. B 38 (1), 127–138.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25 (10), 101302.Google Scholar
Jordan, P. & Colonius, T. 2013 Wave packets and turbulent jet noise. Annu. Rev. Fluid Mech. 45, 173–195.Google Scholar
Karniadakis, G. E. 1990 Spectral element-Fourier methods for incompressible turbulent flows. Comput. Meth. Appl. Mech. Engng 80 (1), 367–380.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.Google Scholar
Karniadakis, G. E. & Sherwin, S. J. 2005 Spectral/hp Methods for Computational Fluid Dynamics. Oxford University Press.Google Scholar
Kolmogorov, A. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Lee, M. J., Kim, J. & Moin, P. 1990 Structure of turbulence at high shear rate. J. Fluid Mech. 216, 561–583.Google Scholar
Longuet-Higgins, M. S. 1981 Oscillating flow over steep sand ripples. J. Fluid Mech. 107, 1–35.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.Google Scholar
Lumley, J. L. 1979 Computational modeling of turbulent flows. Adv. Appl. Mech. 18, 123–176.Google Scholar
Mahesh, K. & Moin, P. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30 (1), 539–578.Google Scholar
Mazzuoli, M. & Vittori, G. 2016 Transition to turbulence in an oscillatory flow over a rough wall. J. Fluid Mech. 792, 67–97.Google Scholar
Mazzuoli, M., Vittori, G. & Blondeaux, P. 2011 Turbulent spots in oscillatory boundary layers. J. Fluid Mech. 685, 365–376.Google Scholar
Mei, C. C. & Liu, P. L. 1993 Surface waves and coastal dynamics. Annu. Rev. Fluid Mech. 25 (1), 215–240.Google Scholar
Nakato, T., Kennedy, J. F., Glover, J. R. & Locher, F. A. 1977 Wave entrainment of sediment from rippled beds. J. Waterways Port Coast. Ocean Div. ASCE 103 (1), 83–99.Google Scholar
Neu, J. C. 1984 The dynamics of stretched vortices. J. Fluid Mech. 143, 253–276.Google Scholar
Nichols, C. S. & Foster, D. L. 2007 Full-scale observations of wave-induced vortex generation over a rippled bed. J. Geophys. Res. 112, C10015.Google Scholar
Nielsen, P. 1992 Coastal Bottom Boundary Layers and Sediment Transport. World Scientific Publishing.Google Scholar
O’Donoghue, T., Doucette, J. S., van der Werf, J. J. & Ribberink, J. S. 2006 The dimensions of sand ripples in full-scale oscillatory flows. Coast. Engng 53 (12), 997–1012.Google Scholar
Okubo, A. 1970 Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences. Deep Sea Res. Ocean Abstracts 17 (3), 445–454.Google Scholar
Ourmieres, Y. & Chaplin, J. R. 2004 Visualizations of the disturbed-laminar wave-induced flow above a rippled bed. Exp. Fluids 36 (6), 908–918.Google Scholar
Ozdemir, C. E., Hsu, T.-J. & Balachandar, S. 2014 Direct numerical simulations of transition and turbulence in smooth-walled Stokes boundary layer. Phys. Fluids 26 (4), 045108.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Rouson, D. W. & Eaton, J. K. 2001 On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 428, 149–169.Google Scholar
Saffman, P. G. 1978 Problems and progress in the theory of turbulence. In Structure and Mechanisms of Turbulence II, pp. 273–306. Springer.Google Scholar
Salon, S., Armenio, V. & Crise, A. 2007 A numerical investigation of the Stokes boundary layer in the turbulent regime. J. Fluid Mech. 570, 253–296.Google Scholar
Saric, W. S. 1994 Görtler vortices. Annu. Rev. Fluid Mech. 26 (1), 379–409.Google Scholar
Sato, S., Mimura, N. & Watanabe, A. 1985 Oscillatory boundary layer flow over rippled beds. In Proceedings of the 19th International Conference on Coastal Engineering, pp. 2293–2309. American Society of Civil Engineers.Google Scholar
Savitzky, A. & Golay, M. J. E. 1964 Smoothing and differentiation of data by simplified least squares procedures. Analyt. Chem. 36 (8), 1627–1639.Google Scholar
Scandura, P., Faraci, C. & Foti, E. 2016 A numerical investigation of acceleration-skewed oscillatory flows. J. Fluid Mech. 808, 576–613.Google Scholar
Scandura, P., Vittori, G. & Blondeaux, P. 2000 Three-dimensional oscillatory flow over steep ripples. J. Fluid Mech. 412, 355–378.Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 567–590.Google Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7 (1), 2778–2784.Google Scholar
Swearingen, J. D. & Blackwelder, R. F. 1987 The growth and breakdown of streamwise vortices in the presence of a wall. J. Fluid Mech. 182, 255–290.Google Scholar
Szabó, B., Düster, A. & Rank, E. 2004 The p-Version of the Finite Element Method. Wiley.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
du Toit, C. G. & Sleath, J. F. A. 1981 Velocity measurements close to rippled beds in oscillatory flow. J. Fluid Mech. 112, 71–96.Google Scholar
Van Atta, C. W. & Antonia, R. A. 1980 Reynolds number dependence of skewness and flatness factors of turbulent velocity derivatives. Phys. Fluids 23 (2), 252–257.Google Scholar
Vittori, G. & Verzicco, R. 1998 Direct simulation of transition in an oscillatory boundary layer. J. Fluid Mech. 371, 207–232.Google Scholar
Vos, P. E. J., Eskilsson, C., Bolis, A., Chun, S., Kirby, R. M. & Sherwin, S. J. 2011 A generic framework for time-stepping partial differential equations (PDEs): general linear methods, object-oriented implementation and application to fluid problems. Intl J. Comput. Fluid Dyn. 25 (3), 107–125.Google Scholar
Weiss, J. 1991 The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D 48 (2–3), 273–294.Google Scholar
van der Werf, J. J., Doucette, J. S., O’Donoghue, T. & Ribberink, J. S. 2007 Detailed measurements of velocities and suspended sand concentrations over full-scale ripples in regular oscillatory flow. J. Geophys. Res. 112, F02012.Google Scholar
van der Werf, J. J., Ribberink, J. S., O’Donoghue, T. & Doucette, J. S. 2006 Modelling and measurement of sand transport processes over full-scale ripples in oscillatory flow. Coast. Engng 53 (8), 657–673.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.Google Scholar
Yuan, J., Dongxu, W. & Madsen, O. S. 2017 A laser-based bottom profiler system for measuring net sediment transport rate in an oscillatory water tunnel. In Proceedings of Coastal Dynamics 2017, pp. 1495–1505.Google Scholar
Zedler, E. A. & Street, R. L. 2006 Sediment transport over ripples in oscillatory flow. J. Hydraul. Engng 132 (2), 180–193.Google Scholar