Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-01T04:22:53.327Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of gravity settling on the onset of thermal convection in a nanofluid-saturated porous medium layer

Published online by Cambridge University Press:  26 March 2024

An-Cheng Ruo Open the ORCID record for An-Cheng Ruo [Opens in a new window]  and
Min-Hsing Chang Open the ORCID record for Min-Hsing Chang [Opens in a new window]
An-Cheng Ruo
Affiliation:
Department of Mechanical and Electro-Mechanical Engineering, National Ilan University, Yilan 260, Taiwan
Min-Hsing Chang*
Affiliation:
Department of Energy Engineering, National United University, Miaoli 360, Taiwan
*
†Email address for correspondence: mhchang@nuu.edu.tw
Get access Rights & Permissions [Opens in a new window]

Abstract

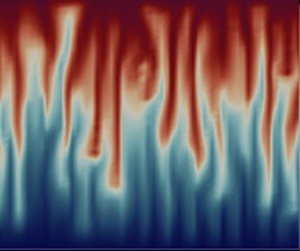
The onset of convection in a horizontal porous medium layer saturated with a nanofluid and heated from below is investigated via linear stability analysis and numerical simulation. The Darcy–Buongiorno model is used to describe the convective transport behaviour of the nanofluid and the settling effect of nanoparticles due to gravity is considered in addition to thermophoresis and Brownian diffusion. The linear stability analysis shows that the gravity settling is a substantial stabilizing mechanism restraining the destabilizing factors such as thermal buoyancy and thermophoresis. The stability threshold is determined by the relative strength of thermophoresis to gravity settling. It is found that the system is destabilized when the thermophoretic mobility prevails. As the nanoparticle size increases, the gravity settling effect is promoted and makes the system more stable. In particular, the onset of instability is dominated by the oscillatory mode once the nanoparticle concentration is in a stably stratified profile across the porous layer. When the Rayleigh–Darcy number $Ra_D$ exceeds the critical value, the spectrum of the growth rates of the unstable modes rises with increasing $Ra_D$ and $Rn$ (i.e. the concentration Rayleigh number), and eventually the unstable modes in the high-wavenumber region exhibit the same instability. The evolution of the convection is further examined by numerical simulation. The results verify the stability characteristics predicted by linear stability analysis. Moreover, the pattern of fingering convection of the nanofluid concentration is observed once the nanofluid concentration is unstably stratified and the density difference across the porous layer is large enough.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection in porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 984 , 10 April 2024 , A5
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aglawe, K.R., Yadav, R.K. & Thool, S.B. 2021 Preparation, applications and challenges of nanofluids in electronic cooling: a systematic review. Mater. Today-Proc. 43 (1), 366–372.CrossRefGoogle Scholar
Ambreen, T. & Kim, M.-H. 2020 Influence of particle size on the effective thermal conductivity of nanofluids: a critical review. Appl. Energy 264, 114684.Google Scholar
Boyd, J.P. 1989 Chebyshev and fourier spectral methods. In Lecture Notes in Engineering (ed. C.A. Brebbia & S.A. Orszag), vol. 49. Springer.CrossRefGoogle Scholar
Buongiorno, J. 2006 Convective transport in nanofluids. Trans. ASME J. Heat Transfer 128, 240–250.CrossRefGoogle Scholar
Canuto, C., Hussaini, M.Y., Quarteroni, A. & Zang, T.A. 2007 Spectral Methods-Evolution to Complex Geometries and Applications to Fluid Dynamics. Springer.CrossRefGoogle Scholar
Chang, M.-H. & Ruo, A.-C. 2022 Rayleigh–Bénard instability in nanofluids: effect of gravity settling. J. Fluid Mech. 950, A37.CrossRefGoogle Scholar
De Paoli, M. 2023 Convective mixing in porous media: a review of Darcy, pore-scale and Hele–Shaw studies. arXiv:2310.01999.Google Scholar
Dukhan, N. 2023 Forced convection of nanofluids in metal foam: an essential review. Intl J. Therm. Sci. 187, 108156.CrossRefGoogle Scholar
Elias, M.M., Miqdad, M., Mahbubul, I.M., Saidur, R., Kamalisarvestani, M., Sohel, M.R., Hepbasli, A., Rahim, N.A. & Amalina, M.A. 2013 Effect of nanoparticle shape on the heat transfer and thermodynamic performance of a shell and tube heat exchanger. Intl Commun. Heat Mass Transfer 44, 93–99.Google Scholar
Ghaziani, N.O. & Hassanipour, F. 2017 Convective heat transfer of $\mbox {Al}_2\mbox {O}_3$ nanofluids in porous media. Trans. ASME J. Heat Transfer 139, 032601.CrossRefGoogle Scholar
Hewitt, D.R. 2020 Vigorous convection in porous media. Proc. R. Soc. A 476, 20200111.CrossRefGoogle ScholarPubMed
Hewitt, D.R., Neufeld, J.A. & Lister, J.R. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.CrossRefGoogle Scholar
Hewitt, D.R., Neufeld, J.A. & Lister, J.R. 2014 High Rayleigh number convection in a three dimensional porous medium. J. Fluid Mech. 748, 879–895.CrossRefGoogle Scholar
Ho, C.-J., Liu, W.-K., Chang, Y.-S. & Lin, C.-C. 2010 Natural convection heat transfer of alumina-water nanofluid in vertical square enclosures: an experimental study. Intl J. Therm. Sci. 49, 1345–1353.CrossRefGoogle Scholar
Huppert, H.E. & Turner, J.S. 1981 Double-diffusive convection. J. Fluid Mech. 106, 299–329.CrossRefGoogle Scholar
Kasaeian, A., Daneshazarian, R., Mahian, O., Koisi, L., Chamkha, A.J., Wongwises, S. & Pop, I. 2017 Nanofluid flow and heat transfer in porous media: a review of the latest developments. Intl J. Heat Mass Transfer 107, 778–791.CrossRefGoogle Scholar
Keblinski, P., Phillpot, S.R., Choi, S.U. & Eastman, J.A. 2002 Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids). Intl J. Heat Mass Transfer 45, 855–863.CrossRefGoogle Scholar
Keblinski, P., Prasher, R. & Eapen, J. 2008 Thermal conductance of nanofluids: is the controversy over? J. Nanopart. Res. 10, 1089–1097.Google Scholar
Kumar, R., Sharma, J. & Sood, J. 2020 Rayleigh–Bénard cell formation of green synthesized nano-particles of silver and selenium. Mater. Today-Proc. 28, 1781–1787.CrossRefGoogle Scholar
Kuznetsov, A.V. & Nield, D.A. 2010 Thermal instability in a porous medium layer saturated by a nanofluid: Brinkman model. Transp. Porous Med. 81, 409–422.CrossRefGoogle Scholar
Liang, Y., Wen, B., Hesse, M.A. & Dicarlo, D. 2018 Effect of dispersion on solutal convection in porous media. Geophys. Res. Lett. 45, 9690–9698.Google Scholar
Mahdi, R.A., Mohammed, H.A., Munisamy, K.M. & Saeid, N.H. 2015 Review of convection heat transfer and fluid flow in porous media with nanofluid. Renew. Sustain. Energy Rev. 41, 715–734.Google Scholar
Michaelides, E.E. 2016 Wall effects on the Brownian movement, thermophoresis, and deposition of nanoparticles in liquids. J. Fluids Engng 135, 051303.Google Scholar
Michaelides, E.E. 2017 Nanoparticle diffusivity in narrow cylindrical pores. Intl J. Heat Mass Transfer 114, 607–612.CrossRefGoogle Scholar
Nield, D.A. & Bejan, A. 2017 Convection in Porous Media. Springer.Google Scholar
Nield, D.A. & Kuznetsov, A.V. 2009 Thermal instability in a porous medium layer saturated by a nanofluid. Intl J. Heat Mass Transfer 52, 5796–5801.CrossRefGoogle Scholar
Nield, D.A. & Kuznetsov, A.V. 2010 The onset of convection in a horizontal nanofluid layer of finite depth. Eur. J. Mech. B/Fluids 29, 217–233.CrossRefGoogle Scholar
Nield, D.A. & Kuznetsov, A.V. 2014 Thermal instability in a porous medium layer saturated by a nanofluid: a revised model. Intl J. Heat Mass Transfer 68, 211–214.CrossRefGoogle Scholar
Rashidi, S., Eskandarian, M., Mahian, O. & Poncet, S. 2019 Combination of nanofluid and inserts for heat transfer enhancement. Therm. Anal. Calorim. 135, 437–460.Google Scholar
Ruo, A.-C., Yan, W.-M. & Chang, M.-H. 2021 The onset of natural convection in a horizontal nanofluid layer heated from below. Heat Transfer 50 (8), 7764–7783.CrossRefGoogle Scholar
Ruo, A.-C., Yan, W.-M. & Chang, M.-H. 2023 A revised work on the Rayleigh–Bénard instability of nanofluid in a porous medium layer. J. Nanofluids 12, 1720–1728.CrossRefGoogle Scholar
Shah, T.R. & Muhammad, H.A. 2019 Applications of hybrid nanofluids in solar energy, practical limitations and challenges: a critical review. Solar Energy 183, 173–203.CrossRefGoogle Scholar
Tzou, D.-Y. 2008 a Instability of nanofluids in natural convection. Trans. ASME J. Heat Transfer 130, 072401.CrossRefGoogle Scholar
Tzou, D.-Y. 2008 b Thermal instability of nanofluids in natural convection. Intl J. Heat Mass Transfer 51, 2967–2979.CrossRefGoogle Scholar
Wen, B., Corson, L. & Chini, G. 2015 Structure and stability of steady porous medium convection at large Rayleigh number. J. Fluid Mech. 772, 197–224.Google Scholar
Yadav, D. 2020 Numerical solution of the onset of buoyancy-driven nanofluid convective motion in an anisotropic porous medium layer with variable gravity and internal heating. Heat Transfer 49 (3), 1170–1191.CrossRefGoogle Scholar
Yadav, D., Chu, Y.M. & Li, Z. 2023 Examination of the nanofluid convective instability of vertical constant throughflow in a porous medium layer with variable gravity. Appl. Nanosci. 13, 353–366.Google Scholar
Yazid, M.N.A.W.M., Sidik, N.A.C. & Yahya, W.J. 2017 Heat and mass transfer characteristics of carbon nanotube nanofluids: a review. Renew. Sustain. Energy Rev. 80, 914–941.CrossRefGoogle Scholar
Zhang, W., Li, W. & Nakayama, A. 2015 An analytical consideration of steady-state forced convection within a nanofluid-saturated metal foam. J. Fluid Mech. 769, 590–620.Google Scholar
Supplementary material: File

Ruo and Chang supplementary movie 1

(Fig 21) The evolution of oscillatory flow patterns at Rn = 25 and RaD = 62 for the case dp = 60 nm
Download Ruo and Chang supplementary movie 1(File)
File 2.7 MB
Supplementary material: File

Ruo and Chang supplementary movie 2

(Fig 22) Temporal evolution of nanofluid concentration for the case dp = 60 nm at Rn = 25 and RaD = 62.
Download Ruo and Chang supplementary movie 2(File)
File 2.7 MB