Hostname: page-component-848d4c4894-p2v8j Total loading time: 0.001 Render date: 2024-06-01T16:32:37.104Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of Stuart vortices in rotating stratified fluids

Published online by Cambridge University Press:  16 May 2024

Yuji Hattori Open the ORCID record for Yuji Hattori [Opens in a new window]  and
Makoto Hirota
Yuji Hattori*
Affiliation:
Institute of Fluid Science, Tohoku University, Sendai 980–8577, Japan
Makoto Hirota
Affiliation:
Institute of Fluid Science, Tohoku University, Sendai 980–8577, Japan
*
†Email address for correspondence: hattori@ifs.tohoku.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

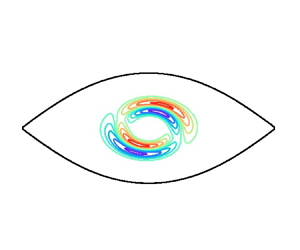
The linear stability of the Stuart vortices, which is a model of arrays of vortices often observed in the atmosphere and the oceans, in rotating stratified fluids is investigated by local and modal stability analysis. As in the case of the two-dimensional (2-D) Taylor–Green vortices, five types of instability appear in general: the pure-hyperbolic instability, the strato-hyperbolic instability, the rotational-hyperbolic instability, the centrifugal instability and the elliptic instability. The condition for each instability and the estimate of the growth rate derived by Hattori & Hirota (J. Fluid Mech., vol. 967, 2023, A32) are shown to also be useful for the Stuart vortices, which supports their applicability to general flows. The properties of each instability depend on stratification and rotation in a way similar to the case of the 2-D Taylor–Green vortices. For the Stuart vortices, however, the centrifugal instability and the elliptic instability become more dominant than the three hyperbolic instabilities in comparison to the 2-D Taylor–Green vortices; this is explained by the larger ratios of the maximum vorticity and the strain rate at the elliptic stagnation points to the strain rate at the hyperbolic stagnation points. Direct correspondence between the modal and local stability results is further established by comparing unstable modes to solutions to the local stability equations; this is useful for identifying the types of modes since the mechanism of instability is readily known in the local stability analysis. This helps us to discover the modes of the ring-type elliptic instability, which have been predicted only theoretically.

JFM classification

Vortex Flows: Vortex instability Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 987 , 25 May 2024 , A12
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aravind, H.M., Dubos, T. & Mathur, M. 2022 Local stability analysis of homogeneous and stratified Kelvin–Helmholtz vortices. J. Fluid Mech. 943, A18.CrossRefGoogle Scholar
Arratia, C., Caulfield, C.P. & Chomaz, J.-M. 2013 Transient perturbation growth in time-dependent mixing layers. J. Fluid Mech. 717, 90–133.CrossRefGoogle Scholar
Aspden, J.M. & Vanneste, J. 2009 Elliptical instability of a rapidly rotating, strongly stratified fluid. Phys. Fluids 21, 074104.CrossRefGoogle Scholar
Bayly, B.J., Holm, D.D. & Lifschitz, A. 1996 Three-dimensional stability of elliptical vortex columns in external strain flows. Phil. Trans. R. Soc. Lond. A 354, 895–926.Google Scholar
Billant, P. 2000 Zigzag instability of vortex pairs in stratified and rotating fluids. Part 1. General stability equations. J. Fluid Mech. 660, 354–395.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2000 a Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 418, 167–188.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2000 b Theoretical analysis of the zigzag instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 419, 29–63.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2000 c Three-dimensional stability of a vertical columnar vortex pair in a stratified fluid. J. Fluid Mech. 419, 65–91.CrossRefGoogle Scholar
Billant, P., Deloncle, A., Chomaz, J.-M. & Otheguy, P. 2010 Zigzag instability of vortex pairs in stratified and rotating fluids. Part 2. Analytical and numerical analyses. J. Fluid Mech. 660, 396–429.CrossRefGoogle Scholar
Deloncle, A., Billant, P. & Chomaz, J.-M. 2008 Nonlinear evolution of the zigzag instability in stratified fluids: a shortcut on the route to dissipation. J. Fluid Mech. 599, 229–239.CrossRefGoogle Scholar
Donnadieu, C., Ortiz, S., Chomaz, J.-M. & Billant, P. 2009 Three-dimensional instabilities and transient growth of a counter-rotating vortex pair. Phys. Fluids 21, 094102.CrossRefGoogle Scholar
Edwards, W.S., Tuckerman, L.S., Friesner, R.A. & Sorensen, D.C. 1994 Krylov methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 110, 82–102.CrossRefGoogle Scholar
Etling, D. 1989 On atmospheric vortex streets in the wake of large islands. Meteorol. Atmos. Phys. 41, 157–164.CrossRefGoogle Scholar
Friedlander, S. & Vishik, M.M. 1991 Instability criteria for the flow of an inviscid incompressible fluid. Phys. Rev. Lett. 66, 2204–2206.CrossRefGoogle ScholarPubMed
Gau, T. & Hattori, Y. 2014 Modal and non-modal stability of two-dimensional Taylor–Green vortices. Fluid Dyn. Res. 46, 031410.CrossRefGoogle Scholar
Godeferd, F.S., Cambon, C. & Leblanc, S. 2001 Zonal approach to centrifugal, elliptic and hyperbolic instabilities in Stuart vortices with external rotation. J. Fluid Mech. 449, 1–37.CrossRefGoogle Scholar
Guimbard, D., Le Dizès, S., Le Bars, M., Le Gal, P. & Leblanc, S. 2010 Elliptic instability of a stratified fluid in a rotating cylinder. J. Fluid Mech. 660, 240–257.CrossRefGoogle Scholar
Hattori, Y. 2016 Concentration of vorticity in a destabilized vortex due to selective decay. J. Fluid Mech. 797, 630–643.CrossRefGoogle Scholar
Hattori, Y. 2018 Concentration of vorticity due to selective decay in doubly periodic vortices and a vortex pair. Fluid Dyn. Res. 50, 011405.CrossRefGoogle Scholar
Hattori, Y. & Fukumoto, Y. 2003 Short-wavelength stability analysis of thin vortex rings. Phys. Fluids 15, 3151–3163.CrossRefGoogle Scholar
Hattori, Y. & Hijiya, K. 2010 Short-wavelength stability analysis of Hill's vortex with/without swirl. Phys. Fluids 20, 074104.CrossRefGoogle Scholar
Hattori, Y. & Hirota, M. 2023 Stability of two-dimensional Taylor–Green vortices in rotating stratified fluids. J. Fluid Mech. 967, A32.CrossRefGoogle Scholar
Hattori, Y., Suzuki, S., Hirota, M. & Khandelwal, M. 2021 Modal stability analysis of arrays of stably stratified vortices. J. Fluid Mech. 909, A4.CrossRefGoogle Scholar
Julien, S., Ortiz, S. & Chomaz, J.-M. 2004 Secondary instability mechanisms in the wake of a flat plate. Eur. J. Mech. (B/Fluids) 23, 157–165.CrossRefGoogle Scholar
Kloosterziel, R.C. & van Heijst, G.J.F. 1991 An experimental study of unstable barotropic vortices in a rotating fluid. J. Fluid Mech. 223, 1–24.CrossRefGoogle Scholar
Leblanc, S. 1997 Stability of stagnation points in rotating flows. Phys. Fluids 9, 3566–3569.CrossRefGoogle Scholar
Leblanc, S. 2000 Internal wave resonances in strain flows. J. Fluid Mech. 477, 259–283.Google Scholar
Leblanc, S. & Cambon, C. 1998 Effects of the Coriolis force on the stability of Stuart vortices. J. Fluid Mech. 356, 353–379.CrossRefGoogle Scholar
Leblanc, S. & Godeferd, F.S. 1999 An illustration of the link between ribs and hyperbolic instability. Phys. Fluids 11, 497–499.CrossRefGoogle Scholar
Le Dizès, S. 2008 Inviscid waves on a Lamb–Oseen vortex in a rotating stratified fluid: consequences for the elliptic instability. J. Fluid Mech. 597, 283–303.CrossRefGoogle Scholar
Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21, 096602.CrossRefGoogle Scholar
Leweke, T. & Williamson, C.H.K. 1998 Three-dimensional instabilities in wake transition. Eur. J. Mech. (B/Fluids) 17, 571–586.CrossRefGoogle Scholar
Lifschitz, A. & Hameiri, E. 1991 Local stability conditions in fluid dynamics. Phys. Fluids A 3, 2644–2651.CrossRefGoogle Scholar
Lifschitz, A. & Hameiri, E. 1993 Localized instabilities of vortex rings with swirl. Commun. Pure Appl. Maths 46, 1379–1408.CrossRefGoogle Scholar
Miyazaki, T. 1993 Elliptical instability in a stably stratified rotating fluid. Phys. Fluids A 5, 2702–2709.CrossRefGoogle Scholar
Miyazaki, T. & Adachi, K. 1998 Short-wavelength instabilities of waves in rotating stratified fluids. Phys. Fluids 10, 3168–3177.CrossRefGoogle Scholar
Miyazaki, T. & Fukumoto, Y. 1992 Three-dimensional instability of strained vortices in a stably stratified flow. Phys. Fluids A 4, 2515–2522.CrossRefGoogle Scholar
Otheguy, P., Billant, P. & Chomaz, J.-M. 2006 a Elliptic and zigzag instabilities on co-rotating vertical vortices in a stratified fluid. J. Fluid Mech. 553, 253–272.CrossRefGoogle Scholar
Otheguy, P., Billant, P. & Chomaz, J.-M. 2006 b The effect of planetary rotation on the zigzag instability of co-rotating vortices in a stratified fluid. J. Fluid Mech. 553, 273–281.CrossRefGoogle Scholar
Park, J. & Billant, P. 2013 Instabilities and waves on a columnar vortex in a strongly stratified and rotating fluid. Phys. Fluids 25, 086601.CrossRefGoogle Scholar
Peyret, R. 2010 Spectral Methods for Incompressible Viscous Flow. Springer.Google Scholar
Pierrehumbert, R.T. & Widnall, S.E. 1982 The two- and three-dimensional instabilities of a spatially periodic shear layer. J. Fluid Mech. 114, 59–82.CrossRefGoogle Scholar
Potylitsin, P.G. & Peltier, W.R. 1998 Stratification effects on the stability of columnar vortices on the $f$-plane. J. Fluid Mech. 355, 45–79.CrossRefGoogle Scholar
Potylitsin, P.G. & Peltier, W.R. 1999 Three-dimensional destabilization of Stuart vortices: the influence of rotation and ellipticity. J. Fluid Mech. 387, 205–226.CrossRefGoogle Scholar
Pralits, J.O., Giannetti, F. & Brandt, L. 2013 Three-dimensional instability of the flow around a rotating circular cylinder. J. Fluid Mech. 730, 5–18.CrossRefGoogle Scholar
Rayleigh, Lord 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Sipp, D. & Jacquin, L. 1998 Elliptic instability in two-dimensional flattened Taylor–Green vortices. Phys. Fluids 10, 839–849.CrossRefGoogle Scholar
Sipp, D., Lauga, E. & Jacquin, L. 1999 Vortices in rotating systems: centrifugal, elliptic and hyperbolic type instabilities. Phys. Fluids 11, 3716–3728.CrossRefGoogle Scholar
Stegner, A., Pichon, T. & Beunier, M. 2005 Elliptical-inertial instability of rotating Kármán vortex streets. Phys. Fluids 17, 066602.CrossRefGoogle Scholar
Suzuki, S., Hirota, M. & Hattori, Y. 2018 Strato-hyperbolic instability: a new mechanism of instability in stably stratified vortices. J. Fluid Mech. 854, 293–323.CrossRefGoogle Scholar
Thorpe, S.A. 2005 The Turbulent Ocean, chap. 13. Cambridge University Press.CrossRefGoogle Scholar
Waite, M.L. & Smolarkiewicz, P.K. 2008 Instability and breakdown of a vertical vortex pair in a strongly stratified fluid. J. Fluid Mech. 606, 239–273.CrossRefGoogle Scholar
Yim, E. & Billant, P. 2016 Analogies and differences between the stability of an isolated pancake vortex and a columnar vortex in stratified fluid. J. Fluid Mech. 796, 732–766.CrossRefGoogle Scholar
Youssef, A. & Marcus, P.S. 2003 The dynamics of Jovian white ovals from formation to merger. Icarus 162, 74–93.CrossRefGoogle Scholar