Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-06-09T02:35:44.521Z Has data issue: false hasContentIssue false
  • English
  • Français

COSUPPORT FOR COMPACTLY GENERATED TRIANGULATED CATEGORIES

Part of: Commutative algebra: Homological methods Abelian categories

Published online by Cambridge University Press:  13 December 2022

XIAOYAN YANG
XIAOYAN YANG*
Affiliation:
Department of Mathematics, Northwest Normal University, Lanzhou 730070, PR China
*
e-mail: yangxy@nwnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

The goal of the article is to better understand cosupport in triangulated categories since it is still quite mysterious. We study boundedness of local cohomology and local homology functors using Koszul objects, give some characterizations of cosupport, and get some results that, in special cases, recover and generalize the known results about the usual cosupport. Additionally, we include some computations of cosupport and provide a comparison of support and cosupport for cohomologically finite objects. Finally, we assign to any object of the category a subset of 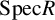$\mathrm {Spec}R$, called the big cosupport, and study some of its properties.

Keywords

cosupportsupportKoszul object

MSC classification

Primary: 13D45: Local cohomology 18E35: Localization of categories
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 116 , Issue 1 , February 2024 , pp. 128 - 144
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Oded Yacobi

This research was partially supported by National Natural Science Foundation of China (11901463).

References

Asadollahi, J., Salarian, S. and Sazeedeh, R., ‘On the local cohomology and support for triangulated categories’, Kyoto J. Math. 51 (2011), 811–829.CrossRefGoogle Scholar
Avramov, L. L., ‘Modules of finite virtual projective dimension’, Invent. Math. 96 (1989), 71–101.CrossRefGoogle Scholar
Avramov, L. L. and Buchweitz, R. O., ‘Support varieties and cohomology over complete intersections’, Invent. Math. 142 (2000), 285–318.CrossRefGoogle Scholar
Avramov, L. L. and Iyengar, S. B., ‘Constructing modules with prescribed cohomological support’, Illinois J. Math. 51 (2007), 1–20.CrossRefGoogle Scholar
Benson, D. J., Iyengar, S. B. and Krause, H., ‘Local cohomology and support for triangulated categories’, Ann. Sci. Éc. Norm. Supér. (4) 41 (2008), 573–619.Google Scholar
Benson, D. J., Iyengar, S. B. and Krause, H., ‘Stratifying triangulated categories’, J. Topol. 4 (2011), 641–666.CrossRefGoogle Scholar
Benson, D. J., Iyengar, S. B. and Krause, H., ‘Colocalising subcategories and cosupport’, J. reine angew. Math. 673 (2012), 161–207.Google Scholar
Benson, D. J., Iyengar, S. B. and Krause, H., ‘A local-global principle for small triangulated categories’, Math. Proc. Cambridge Philos. Soc. 158 (2015), 451–476.CrossRefGoogle Scholar
Bruns, W. and Herzog, J., Cohen–Macaulay Rings, Cambridge Studies in Advanced Mathematics, 39 (Cambridge University Press, UK, 1993).Google Scholar
Carlson, J. F., ‘The varieties and the cohomology ring of a module’, J. Algebra 85 (1983), 104–143.CrossRefGoogle Scholar
Enochs, E. E. and Jenda, O. M. G., Relative Homological Algebra (Walter de Gruyter, Berlin–New York, 2000).CrossRefGoogle Scholar
Erdmann, K., Holloway, M., Snashall, N., Solberg, O. and Taillefer, R., ‘Support varieties for selfinjective algebras’, K-Theory 33 (2004), 67–87.CrossRefGoogle Scholar
Foxby, H.-B. and Iyengar, S. B., ‘Depth and amplitude for unbounded complexes’, Contemp. Math. 331 (2003), 119–137.CrossRefGoogle Scholar
Friedlander, E. M. and Parshall, B. J., ‘Support varieties for restricted Lie algebras,’ Invent. Math. 86 (1986), 553–562.CrossRefGoogle Scholar
Friedlander, E. M. and Pevtsova, J., ‘Representation theoretic support spaces for finite group schemes’, Amer. J. Math. 127 (2005), 379–420.CrossRefGoogle Scholar
Friedlander, E.M. and Pevtsova, J., ‘ $\pi$ -supports for modules for finite group schemes’, Duke Math. J. 139 (2007), 317–368.CrossRefGoogle Scholar
Krause, H., ‘Thick subcategories of modules over commutative Noetherian rings’, Math. Ann. 340 (2008), 733–747.CrossRefGoogle Scholar
Neeman, A., Triangulated Categories, Annals of Mathematics Studies, 148 (Princeton University Press, Princeton, NJ, 2001).CrossRefGoogle Scholar
Quillen, D., ‘The spectrum of an equivariant cohomology ring. I, II’, Ann. of Math. (2) 94 (1971), 549–572; ibid. 94 (1971), 573–602.CrossRefGoogle Scholar
Sather-Wagstaff, S. and Wicklein, R., ‘Support and adic finiteness for complexes’, Comm. Algebra 45 (2017), 2569–2592.CrossRefGoogle Scholar
Shaul, L., ‘The Cohen–Macaulay property in derived commutative algebra’, Trans. Amer. Math. Soc. 373 (2020), 6095–6138.CrossRefGoogle Scholar