Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-08T01:22:42.822Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansion and dimension

Published online by Cambridge University Press:  09 April 2009

Vincent J. Mancuso
Vincent J. Mancuso
Affiliation:
Department of Mathematics, St. John's University, Jamaica,New York,11439, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If (X, τ) is a topological space, 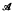is a family of subsets of X, then the expansion of τ by 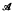is the topology τ(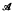) on X having τ ∪ 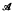as a subbase. If (X, τ) has property 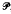, when does (X, τ(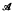)) have property 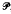? In this paper we answer this question for the property 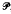of dimension. We apply our techniques to first countability and related properties.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 22 , Issue 3 , November 1976 , pp. 313 - 320
Copyright
Copyright © Australian Mathematical Society 1976

References

Anderson, D. R. (1965), ‘On connected irresolvable Hausdorff spaces’, Proc. Amer. Math. Soc. 16, 463–466.CrossRefGoogle Scholar
Borges, C. J. (1967), ‘On extensions of topologies’, Canad. J. Math. 19, 474–487.CrossRefGoogle Scholar
Dowker, C. H. (1952), ‘Inductive dimension of completely normal spaces’, Quart. J. Math. (2) 4, 267–281.CrossRefGoogle Scholar
Engelking, R. (1968), Outline of General Topology (Wiley, New York).Google Scholar
Franklin, S. P. (1965), ‘Spaces in which sequences suffice’, Fund. Math. 57, 107–116.CrossRefGoogle Scholar
Franklin, S. P. (1969), ‘On two questions of Moore and Mrowka’, Proc. Amer. Math. Soc. 21, 597–599.CrossRefGoogle Scholar
Guthrie, J. A. and Stone, H. E. (1972), ‘Expansions of mappings’, Second Pittsburgh International Conference, Lecture Notes in Mathematics, Springer-Verlag 378, 164–171.Google Scholar
Guthrie, J. A. and Stone, H. E. (1973), ‘Spaces whose connected expansions preserve connected subsets’, Fund. Math. 80, 91–100.CrossRefGoogle Scholar
Guthrie, J. A., Reynolds, D. F. and Stone, H. E. (1973), ‘Connected expansions of topologies’, Bull. Austral. Math. Soc. 9, 259–265.CrossRefGoogle Scholar
Levine, N. (1964), ‘Simple extensions of topologies’, Amer. Math Monthly 71, 22–25.CrossRefGoogle Scholar
Levine, N. (1966), ‘On families of topologies for a set’, Amer. Math, Monthly 73, 358–361.CrossRefGoogle Scholar
Michael, E. (1972), ‘A quintuple quotient quest’, Gen. Topology Appl. 2, 91–138.CrossRefGoogle Scholar
Nagami, K. (1970), Dimension Theory (Academic Press, New York).Google Scholar
Nagata, J. (1965), Modem Dimension Theory (Wiley, New York).Google Scholar
Ju., Orevkov (1962), ‘Totally bounded metric spaces’, Soviet Math. Dokl. 3, 386–387.Google Scholar
Reynolds, D. F. (preprint) ‘Preservation of connectedness under extensions of topologies’.Google Scholar
Siwiec, F. (1971), ‘Sequence covering and countably bi-quotient mappings’, Gen. Topology Appl. 1, 143–154.CrossRefGoogle Scholar
Steen, L. A. and Seebach, J. A. Jr, (1970), Counterexamples in Topology (Holt, Rhinehart and Winston, New York).Google Scholar