Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-06-10T00:43:40.339Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITE TWO-DISTANCE-TRANSITIVE DIHEDRANTS

Part of: Algebraic combinatorics Permutation groups

Published online by Cambridge University Press:  26 January 2022

WEI JIN  and
LI TAN
WEI JIN*
Affiliation:
School of Statistics, Jiangxi University of Finance and Economics, Nanchang, Jiangxi330013, P.R. China School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha, Hunan410075, P.R. China
LI TAN
Affiliation:
School of Statistics, Jiangxi University of Finance and Economics, Nanchang, Jiangxi330013, P.R. China e-mail: tltanli@126.com
*
e-mail: jinwei@jxufe.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

A noncomplete graph is 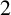$2$ -distance-transitive if, for 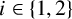$i \in \{1,2\}$ and for any two vertex pairs 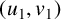$(u_1,v_1)$ and 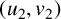$(u_2,v_2)$ with the same distance i in the graph, there exists an element of the graph automorphism group that maps 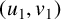$(u_1,v_1)$ to 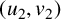$(u_2,v_2)$ . This paper determines the family of 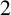$2$ -distance-transitive Cayley graphs over dihedral groups, and it is shown that if the girth of such a graph is not 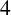$4$ , then either it is a known 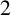$2$ -arc-transitive graph or it is isomorphic to one of the following two graphs: 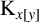$ {\mathrm {K}}_{x[y]}$ , where 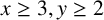$x\geq 3,y\geq 2$ , and 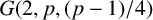$G(2,p,({p-1})/{4})$ , where p is a prime and 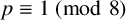$p \equiv 1 \ (\operatorname {mod}\, 8)$ . Then, as an application of the above result, a complete classification is achieved of the family of 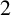$2$ -geodesic-transitive Cayley graphs for dihedral groups.

Keywords

Cayley graph2-distance-transitive graphdihedral group

MSC classification

Primary: 05E18: Group actions on combinatorial structures
Secondary: 20B25: Finite automorphism groups of algebraic, geometric, or combinatorial structures
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 113 , Issue 3 , December 2022 , pp. 386 - 401
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Brian Alspach

Supported by the NNSF of China (12061034,12071484) and NSF of Jiangxi (20212BAB201010,20192ACBL21007,GJJ190273)

References

Alspach, B., Conder, M., Marušič, D. and Xu, M. Y., ‘A classification of 2-arc-transitive circulants’, J. Algebraic Combin. 5 (1996), 83–86.CrossRefGoogle Scholar
Brouwer, A. E., Cohen, A. M. and Neumaier, A., Distance-Regular Graphs (Springer-Verlag, Berlin–Heidelberg–New York, 1989).CrossRefGoogle Scholar
Cameron, P. J., Permutation Groups, London Mathematical Society Student Texts, 45 (Cambridge University Press, Cambridge, 1999).CrossRefGoogle Scholar
Chen, J. Y., Jin, W. and Li, C. H., ‘On 2-distance-transitive circulants’, J. Algebraic Combin. 49 (2019), 179–191.CrossRefGoogle Scholar
Cheng, Y. and Oxley, J., ‘On weakly symmetric graphs of order twice a prime’, J. Combin. Theory Ser. B 42 (1987), 196–211.CrossRefGoogle Scholar
Corr, B., Jin, W. and Schneider, C., ‘Finite two-distance-transitive graphs’, J. Graph Theory 86 (2017), 78–91.CrossRefGoogle Scholar
Devillers, A., Giudici, M., Li, C. H. and Praeger, C. E., ‘Locally $s$ -distance transitive graphs’, J. Graph Theory 69(2) (2012), 176–197.CrossRefGoogle Scholar
Devillers, A., Jin, W., Li, C. H. and Praeger, C. E., ‘Local $2$ -geodesic transitivity and clique graphs’, J. Combin. Theory Ser. A 120 (2013), 500–508.CrossRefGoogle Scholar
Devillers, A., Jin, W., Li, C. H. and Praeger, C. E., ‘Line graphs and $2$ -geodesic transitivity’, Ars Math. Contemp. 6 (2013), 13–20.CrossRefGoogle Scholar
Devillers, A., Jin, W., Li, C. H. and Praeger, C. E., ‘On normal 2-geodesic transitive Cayley graphs’, J. Algebraic Combin. 39 (2014), 903–918.CrossRefGoogle Scholar
Devillers, A., Jin, W., Li, C. H. and Praeger, C. E., ‘Finite 2-geodesic transitive graphs of prime valency’, J. Graph Theory 80 (2015), 18–27.CrossRefGoogle Scholar
Dixon, J. D. and Mortimer, B., Permutation Groups (Springer, New York, 1996).CrossRefGoogle Scholar
Du, S. F., Malnič, A. and Marušič, D., ‘Classification of 2-arc-transitive dihedrants’, J. Combin. Theory Ser. B 98 (2008), 1349–1372.CrossRefGoogle Scholar
Du, S. F., Wang, R. J. and Xu, M. Y., ‘On the normality of Cayley digraphs of order twice a prime’, Australas. J. Combin. 18 (1998), 227–234.Google Scholar
Godsil, C. D., ‘On the full automorphism group of a graph’, Combinatorica 1 (1981), 243–256.CrossRefGoogle Scholar
Godsil, C. D., Liebler, R. A. and Praeger, C. E., ‘Antipodal distance transitive covers of complete graphs’, European J. Combin. 19 (1998), 455–478.CrossRefGoogle Scholar
Ivanov, A. A. and Praeger, C. E., ‘On finite affine 2-arc transitive graphs’, European J. Combin. 14 (1993), 421–444.Google Scholar
Jin, W., Devillers, A., Li, C. H. and Praeger, C. E., ‘On geodesic transitive graphs’, Discrete Math. 338 (2015), 168–173.CrossRefGoogle Scholar
Jin, W., Liu, W. J. and Wang, C. Q., ‘Finite 2-geodesic transitive abelian Cayley graphs’, Graphs Combin. 32 (2016), 713–720.CrossRefGoogle Scholar
Jin, W. and Ma, J. C., ‘Finite $2$ -geodesic-transitive Cayley graphs of dihedral groups’, Ars Combin. 137 (2018), 403–417.Google Scholar
Jin, W. and Tan, L., ‘Two distance transitive graphs of valency six’, Ars Math. Contemp. 11 (2016), 49–58.Google Scholar
Jones, G., ‘Cyclic regular subgroups of primitive permutation groups’, J. Group Theory 5 (2002), 403–407.CrossRefGoogle Scholar
Kwak, J. H. and Oh, J. M., ‘One-regular normal Cayley graphs on dihedral groups of valency 4 or 6 with cyclic vertex stabilizer’, Acta Math. Sin. (Engl. Ser.) 22 (2006), 1305–1320.CrossRefGoogle Scholar
Li, C. H., ‘The finite primitive permutation groups containing an abelian regular subgroup’, Proc. Lond. Math. Soc. (3) 87 (2003), 725–748.Google Scholar
Li, C. H., ‘Finite edge transitive Cayley graphs and rotary Cayley maps’, Trans. Amer. Math. Soc. 358 (2006), 4605–4635.CrossRefGoogle Scholar
Li, C. H. and Pan, J. M., ‘Finite 2-arc-transitive abelian Cayley graphs’, European J. Combin. 29 (2008), 148–158.CrossRefGoogle Scholar
Lu, Z. P. and Xu, M. Y., ‘On the normality of Cayley graphs of order pq ’, Australas. J. Combin. 27 (2003), 81–93.Google Scholar
Marušič, D., ‘On 2-arc-transitivity of Cayley graphs’, J. Combin. Theory Ser. B 87 (2003), 162–196.CrossRefGoogle Scholar
Paley, R. E. A. C., ‘On orthogonal matrices’, J. Math. Phys. 12 (1933), 311–320.CrossRefGoogle Scholar
Pan, J. M., ‘Locally primitive Cayley graphs of dihedral groups’, European J. Combin. 36 (2014), 39–52.CrossRefGoogle Scholar
Pan, J. M., Yu, X., Zhang, H. and Huang, Z. H., ‘Finite edge-transitive dihedrant graphs’, Discrete Math. 312 (2012), 1006–1012.CrossRefGoogle Scholar
Praeger, C. E., ‘An O’Nan–Scott theorem for finite quasiprimitive permutation groups and an application to 2-arc transitive graphs’, J. Lond. Math. Soc. (2) 47(2) (1993), 227–239.Google Scholar
Praeger, C. E., ‘On a reduction theorem for finite, bipartite, 2-arc transitive graphs’, Australas. J. Combin. 7 (1993), 21–36.Google Scholar
Praeger, C. E., ‘Finite normal edge-transitive Cayley graphs’, Bull. Aust. Math. Soc. 60 (1999), 207–220.CrossRefGoogle Scholar
Qiao, Z., Du, S. F. and Koolen, J., ‘2-walk-regular dihedrants from group divisible designs’, Electron. J. Combin. 23(2) (2016), P2.51.CrossRefGoogle Scholar
Song, S. J., Li, C. H. and Zhang, H., ‘Finite permutation groups with a regular dihedral subgroup, and edge-transitive dihedrants’, J. Algebra 399 (2014), 948–959.CrossRefGoogle Scholar
Tutte, W. T., ‘A family of cubical graphs’, Math. Proc. Cambridge Philos. Soc. 43 (1947), 459–474.CrossRefGoogle Scholar
Tutte, W. T., ‘On the symmetry of cubic graphs’, Canad. J. Math. 11 (1959), 621–624.CrossRefGoogle Scholar
Weiss, R., ‘The non-existence of 8-transitive graphs’, Combinatorica 1 (1981), 309–311.CrossRefGoogle Scholar
Wielandt, H., Finite Permutation Groups (Academic Press, New York, 1964).Google Scholar
Xu, M. Y., ‘Automorphism groups and isomorphisms of Cayley digraphs’, Discrete Math. 182 (1998), 309–319.Google Scholar