Hostname: page-component-7dd5485656-j7khd Total loading time: 0 Render date: 2025-10-30T13:59:33.245Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth properties and sequences of zeros of analytic functions in spaces of Dirichlet type

Part of: Linear function spaces and their duals Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  09 April 2009

Daniel Girela  and
José Ángel Peláez
Daniel Girela
Affiliation:
Depto. de Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, Campus de Teatinos, 29071 Málaga, Spain, e-mail: girela@uma.es, pelaez@anamat.cie.uma.es
José Ángel Peláez
Affiliation:
Depto. de Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, Campus de Teatinos, 29071 Málaga, Spain, e-mail: girela@uma.es, pelaez@anamat.cie.uma.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

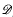For 0 < p < ∞, we let pp−1 denote the space of those functions f that are analytic in the unit disc Δ = {z ∈ C: |z| < 1} and satisfy ∫Δ(1 – |z|)p−1|f′(z)|pdx dy < ∞ The spaces 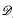pp−1 are closely related to Hardy spaces. We have, 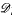p−1p ⊂ Hp, if 0 < p ≦ 2, and Hp ⊂ 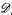pp−1, if 2 ≦ p < ∞. In this paper we obtain a number of results about the Taylor coefficients of pp-1 -functions and sharp estimates on the growth of the integral means and the radial growth of these functions as well as information on their zero sets.

2000 Mathematics subject classification: primary 30D35, 30D55, 46E15.

Keywords

Spaces of Dirichlet typeHardy spacesBergman spacesintegral meansradial growthsequences of zeros.

MSC classification

Secondary: 30D35: Distribution of values, Nevanlinna theory 46E15: Banach spaces of continuous, differentiable or analytic functions

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 80 , Issue 3 , June 2006 , pp. 397 - 418
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Ahlfors, L. V., Complex analysis, 2nd edition (Dover, McGraw-Hill, New York, 1966).Google Scholar
[2]Anderson, J. M., Clunie, J. and Pommerenke, Ch., ‘On Bloch functions and normal functions’, J. Reine Angew. Math. 270 (1974), 12–37.Google Scholar
[3]Arazy, J., Fisher, S. D. and Peetre, J., ‘Möbius invariant function spaces’, J. Reine Angew. Math. 363 (1985), 110–145.Google Scholar
[4]Arcozzi, N., Rochberg, R. and Sawyer, E., ‘Carleson measures for analytic Besov spaces’, Rev. Mat. Iberoamericana 18 (2002), 443–510.CrossRefGoogle Scholar
[5]Aulaskari, R., Xiao, J. and Zhao, R., ‘On subspaces and subsets of BMOA and UBC’, Analysis 15 (1995), 101–121.CrossRefGoogle Scholar
[6]Baernstein, A. II, Girela, D. and Peláez, J. A., ‘Univalent functions, hardy spaces and spaces of Dirichlet type’, Illinois J. Math. 48 (2004), 837–859.CrossRefGoogle Scholar
[7]Buckley, S. M., Koskela, P. and Vukotié, D., ‘Fractional integration, differentiation, and weighted Bergman spaces’. Math. Proc. Cambridge Philos. Soc. 126 (1999), 369–385.CrossRefGoogle Scholar
[8]Choe, B. R., Koo, H. and Smith, W., ‘Composition operators acting on holomorphic Sobolev spaces’, Trans. Amer. Math. Soc. 355 (2003), 2829–2855.CrossRefGoogle Scholar
[9]Doubtsov, E. S., ‘Corrected outer functions’, Proc. Amer Math. Soc. 126 (1998), 515–522.CrossRefGoogle Scholar
[10]Duren, P. L., Theory of Hp spaces, 2nd edition (Dover, Mineola, New York, 2000).Google Scholar
[11]Duren, P. L. and Schuster, A. P., Bergman spaces, Math. Surveys and Monographs 100 (American Mathematical Society, Providence, RI, 2004).CrossRefGoogle Scholar
[12]Flett, T. M., ‘The dual of an inequality of Hardy and Littlewood and some related inequalities’, J. Math. Anal. Appl. 38 (1972), 746–765.CrossRefGoogle Scholar
[13]Garnett, J. B., Bounded analytic functions (Academic Press, New York, 1981).Google Scholar
[14]Girela, D., ‘Growth of the derivative of bounded analytic functions’, Complex Var Theory Appl. 20 (1992), 221–227.Google Scholar
[15]Girela, D., Nowak, M. and Waniurski, P., ‘On the zeros of Bloch functions’, Math. Proc. Camb. Philos. Soc. 129 (2001), 117–128.CrossRefGoogle Scholar
[16]Hayman, W. K., Meromorphic functions, Oxford Mathematical Monographs (Clarendon Press, Oxford, 1964).Google Scholar
[17]Hedenmalm, H., Korenblum, B. and Zhu, K., Theory of Bergman Spaces, Graduate Texts in Mathematics 199 (Springer, New York, 2000).CrossRefGoogle Scholar
[18]Horowitz, C., ‘Zeros of functions in Bergman spaces’, Duke Math. J. 41 (1974), 693–710.CrossRefGoogle Scholar
[19]Littlewood, J. E. and Paley, R. E. A. C., ‘Theorems on Fourier series and power series. II’, Proc. London Math. Soc. 42 (1936), 52–89.Google Scholar
[20]Luecking, D. H., ‘A new proof of an inequality of Littlewood and Paley’, Proc. Amer Math. Soc. 103 (1988), 887–893.CrossRefGoogle Scholar
[21]Mateljevic, M. and Pavlovic, M., ‘Lp-behaviour of power series with positive coefficients and Hardy spaces’, Proc. Amer Math. Soc. 87 (1983), 309–316.Google Scholar
[22]Miao, J., ‘A property of analytic functions with Hadamard gaps’, Bull. Austral. Math. Soc. 45 (1992), 105–112.CrossRefGoogle Scholar
[23]Nevanlinna, R., Analytic functions (Springer, New York, 1970).CrossRefGoogle Scholar
[24]Piranian, G., ‘Bounded functions with large circular variation’, Proc. Amer Math. Soc. 19 (1968), 1255–1257.CrossRefGoogle Scholar
[25]Pommerenke, Ch., ‘Über die Mittelwerte und Koeffizienten multivalenter Funktionen’, Math. Ann. 145 (1962), 285–296.CrossRefGoogle Scholar
[26]Pommerenke, Ch., Univalent functions (Vandenhoeck und Ruprecht, Göttingen, 1975).Google Scholar
[27]Rochberg, R. and Wu, Z. J., ‘Toeplitz operators on Dirichlet spaces’, Integral Equations Operator Theory 15 (1992), 57–75.CrossRefGoogle Scholar
[28]Rochberg, R. and Wu, Z. J., ‘A new characterization of Dirichlet type spaces and applications’, Illinois J. Math. 37 (1993). 101–122.CrossRefGoogle Scholar
[29]Rudin, W., ‘The radial variation of analytic functions’, Duke Math. J. 22 (1955), 235–242.CrossRefGoogle Scholar
[30]Stegenga, D. A., ‘Multipliers of the Dirichlet spaces’, Illinois J. Math. 24 (1980), 113–139.CrossRefGoogle Scholar
[31]Tsuji, M., Potential theory in modern function theory (Chelsea Publ. Co., New York, 1975).Google Scholar
[32]Ullrich, D. C., ‘Khinchin's inequality and the zeroes of Bloch functions’, Duke Math. J. 57 (1988). 519–535.CrossRefGoogle Scholar
[33]Verbitskii, I. E., ‘Inner function as multipliers of the space α’, Funktsional. Anal. i Prilozhen. 16 (1982), 47–48 (in Russian).Google Scholar
[34]Vinogradov, S. A., ‘Multiplication and division in the space of analytic functions with areaintegrable derivative, and in some related spaces’, Zap. Nauchn. Sem. S. -Peterburg. Otdel. Mat. Inst. Steklov. (POMI) (Issled. po Linein. Oper. i Teor. Funktsii 23) 222 (1995), 45–77, 308 (in Russian); translation inGoogle Scholar
J. Math. Sci. (New York) 87 (1997), 3806–3827.CrossRefGoogle Scholar
[35]Weiss, M., ‘The law of the iterated logarithm for lacunary trigonometric series’, Trans. Amer Math. Soc. 91 (1959), 444–469.Google Scholar
[36]Wu, Z., ‘Carleson measures and multipliers for Dirichlet spaces’, J. Funct. Anal. 169 (1999), 148–163.CrossRefGoogle Scholar
[37]Zygmund, A., ‘On certain integrals’, Trans. Amer. Math. Soc. 55 (1944), 170–204.CrossRefGoogle Scholar
[38]Zygmund, A., Trigonometric series, Vol. I and Vol. II, 2nd edition (Cambridge Univ. Press, Cambridge. 1959).Google Scholar