Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-01T22:02:40.232Z Has data issue: false hasContentIssue false
  • English
  • Français

IRREDUCIBLE QUASIORDERS OF MONOUNARY ALGEBRAS

Part of: Graph theory Lattices Ordered structures

Published online by Cambridge University Press:  01 March 2013

DANICA JAKUBÍKOVÁ-STUDENOVSKÁ ,
REINHARD PÖSCHEL  and
SÁNDOR RADELECZKI
DANICA JAKUBÍKOVÁ-STUDENOVSKÁ
Affiliation:
Institute of Mathematics, P.J. Šafárik University, Košice, Slovakia (email: Danica.Studenovska@upjs.sk)
REINHARD PÖSCHEL*
Affiliation:
Institute of Algebra, TU Dresden, Germany (email: reinhard.poeschel@tu-dresden.de)
SÁNDOR RADELECZKI
Affiliation:
Institute of Mathematics, University of Miskolc, Hungary (email: matradi@uni-miskolc.hu)
*
✉For correspondence; e-mail: reinhard.poeschel@tu-dresden.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Rooted monounary algebras can be considered as an algebraic counterpart of directed rooted trees. We work towards a characterization of the lattice of compatible quasiorders by describing its join- and meet-irreducible elements. We introduce the limit 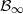$\cB _\infty $ of all 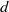$d$-dimensional Boolean cubes 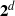$\Two ^d$ as a monounary algebra; then the natural order on 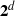$\Two ^d$ is meet-irreducible. Our main result is that any completely meet-irreducible quasiorder of a rooted algebra is a homomorphic preimage of the natural partial order (or its inverse) of a suitable subalgebra of 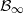$\cB _\infty $. For a partial order, it is known that complete meet-irreducibility means that the corresponding partially ordered structure is subdirectly irreducible. For a rooted monounary algebra it is shown that this property implies that the unary operation has finitely many nontrivial kernel classes and its graph is a binary tree.

Keywords

partial ordermonounary algebraquasiorder latticemeet-irreducible quasiordercritical pairrooted tree

MSC classification

Secondary: 06F99: None of the above, but in this section 06B99: None of the above, but in this section 05C05: Trees
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 93 , Issue 3 , December 2012 , pp. 259 - 276
Copyright
Copyright © 2013 Australian Mathematical Publishing Association Inc. 

References

[1]Czédli, G. and Lenkehegyi, A., ‘On classes of ordered algebras and quasiorder distributivity’, Acta Sci. Math. 46 (1983), 41–54.Google Scholar
[2]Erné, M. and Reinhold, J., ‘Intervals in lattices of quasiorders’, Order 12(4) (1995), 375–403.CrossRefGoogle Scholar
[3]Foldes, S. and Szigeti, J., ‘Maximal compatible extensions of partial orders’, J. Aust. Math. Soc. 81(2) (2006), 245–252.CrossRefGoogle Scholar
[4]Ganter, B. and Wille, R., Formal Concept Analysis – Mathematical Foundations (Springer, Berlin, 1999).CrossRefGoogle Scholar
[5]Jakubíková-Studenovská, D. and Pócs, J., Monounary Algebras (P. J. Šafárik University Košice, 2009).Google Scholar
[6]Jakubíková-Studenovská, D., Pöschel, R. and Radeleczki, S., ‘The lattice of compatible quasiorders of acyclic monounary algebras’, Order 28(3) (2011), 481–497.CrossRefGoogle Scholar
[7]Radeleczki, S. and Szigeti, J., ‘Linear orders on general algebras’, Order 22(4) (2005), 41–62.CrossRefGoogle Scholar
[8]Szigeti, J. and Nagy, B., ‘Linear extensions of partial orders preserving monotonicity’, Order 4(1) (1987), 31–35.CrossRefGoogle Scholar
[9]Trotter, W. T., Combinatorics and Partially Ordered Sets, Dimension Theory (John Hopkins University Press, Baltimore, MD, 1992).CrossRefGoogle Scholar