Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Burns, J. C.
1970.
The iterated equation of generalized axially symmetric potential theory. V. Generalized weinstein correspondence principle.
Journal of the Australian Mathematical Society,
Vol. 11,
Issue. 2,
p.
129.
Burns, J. C.
1974.
The iterated equation of generalized axially symmetric potential theory, VI General solutions.
Journal of the Australian Mathematical Society,
Vol. 18,
Issue. 3,
p.
318.
Rbragg, L.
1974.
Related non-homogeneous partial differential equations.
Applicable Analysis,
Vol. 4,
Issue. 2,
p.
161.
Bragg, L.R
1981.
Abstract Cauchy problems that involve a product of two Euler-Poisson-Darboux operators.
Journal of Differential Equations,
Vol. 41,
Issue. 3,
p.
426.
Bragg, L. R.
1981.
Vector Lifting and Factorable Differential Operators.
SIAM Journal on Mathematical Analysis,
Vol. 12,
Issue. 5,
p.
722.
Bragg, L. R.
1990.
The iterated abstract euler-poisson-darboux problem for negative values of the parameter.
Applicable Analysis,
Vol. 37,
Issue. 1-4,
p.
213.
Urinov, A. K.
and
Karimov, Sh. T.
2020.
On the Cauchy Problem for the Iterated Generalized Two-axially Symmetric Equation of Hyperbolic Type.
Lobachevskii Journal of Mathematics,
Vol. 41,
Issue. 1,
p.
102.
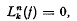 where the operator is defined by
where the operator is defined by