No CrossRef data available.
Article contents
The iterated equation of generalized axially symmetric potential theory, VI General solutions
Published online by Cambridge University Press: 09 April 2009
Extract
The iterated equation of generalized axially symmetric potential theory [1] is the equation 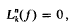 where, in its simplest form, the operator Lk is defined by
where, in its simplest form, the operator Lk is defined by 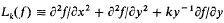 the function f
the function f  f(x, y) being assumed to belong to the class of C2n functions and the parameter l to take any real value. In appropriate circumstances, which will be indicated later, the operator can be generalized but as this can be done without altering the methods used, the operator will be taken in the form
f(x, y) being assumed to belong to the class of C2n functions and the parameter l to take any real value. In appropriate circumstances, which will be indicated later, the operator can be generalized but as this can be done without altering the methods used, the operator will be taken in the form 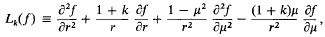 where r, θ are polar coordinates such that x = r cos θ, y = r sin μ = cosθ.
where r, θ are polar coordinates such that x = r cos θ, y = r sin μ = cosθ.
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 18 , Issue 3 , November 1974 , pp. 318 - 327
- Copyright
- Copyright © Australian Mathematical Society 1974




