Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-09T12:23:28.755Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower bound for the number of real roots of a random algebraic polynomial

Part of: Combinatorics

Published online by Cambridge University Press:  09 April 2009

M. N. Mishra ,
N. N. Nayak  and
S. Pattanayak
M. N. Mishra
Affiliation:
School of Mathematical SciencesSambalpur University, Jyoti Vihar, Burla, 768017 Orissa, India
N. N. Nayak
Affiliation:
College of Basic Science and Humanities, O.U.A.T. Bhubaneswar 751005 Puri, Orissa, India
S. Pattanayak
Affiliation:
College of Basic Science and Humanities, O.U.A.T. Bhubaneswar 751005 Puri, Orissa, India
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X1, X2, …, Xn be identically distributed independent random variables belonging to the domain of attraction of the normal law, have zero means and Pr{Xr ≠ 0} > 0. Suppose a0, a1, …, an are non-zero real numbers and max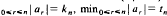 and εn is such that as n → ∞, εn. If Nn be the number of real roots of the equation 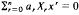then for n > n0, Nn > εn log n outside an exceptional set of measure at most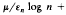 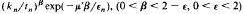provided limn→∞ (kn/tn) is finite.

MSC classification

Secondary: 05A17: Partitions of integers 05A19: Combinatorial identities, bijective combinatorics
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 35 , Issue 1 , August 1983 , pp. 18 - 27
Copyright
Copyright © Australian Mathematical Society 1983

References

Gnedenko, B. V. and Kolmogorov, A. N. (1968), Limit distribution of sums of independent random variables, (Addison Wesley, Inc).Google Scholar
Samal, G. (1962), ‘On the number of real roots of a random algebraic equation’, Proc. Cambridge Philos. Soc. 58, 433–442.CrossRefGoogle Scholar
Samal, G. and Mishra, M. N. (1972a), ‘On the lower bound of the number of real roots of a random algebraic equation with infinite variance’, Proc. Amer. Math. Soc. 33, 523–528.CrossRefGoogle Scholar
Samal, G. and Mishra, M. N. (1972b), ‘On the lower bound of the number of real roots of a random algebraic equation with infinite variance II, Proc. Amer. Math. Soc. 36, 557–563.CrossRefGoogle Scholar
Samal, G. and Mishra, M. N. (1973), ‘On the lower bound of the number of real roots of a random algebraic equation with infinite variance III, Proc. Amer. Math. Soc. 39, 184–189.CrossRefGoogle Scholar
Ibragimov, I. A. and Linnik, Yu. V. (1972), Independent and stationary sequences of random variables (Wolters-Noordhoff, Groningen).Google Scholar
Ibragimov, I. A. and Maslova, N. B. (1971), ‘On the expected number of real zeros of random algebraic polynomials I, Coefficient with zero means’ (translated by B. Seckler), Theory of Probability and its Applications, Vol. XVI, 2, 228–248.CrossRefGoogle Scholar
Littlewood, J. E. and Offord, A. C. (1939), ‘On the number of real roots of a random algebraic equation II’, Proc. Cambridge Philos. Soc. 35, 133–148.CrossRefGoogle Scholar
Dunnage, J. E. A. (1978), ‘The number of real roots of a class of random algebraic polynomial’, Proc. London Math. Soc. (3) 18, 439–460.Google Scholar
Dunnage, J. E. A. (1970), ‘The number of real zeros of a class of random algebraic polynomial II’, Quart. J. Math. Oxford Ser. (2) 21, 309–319.CrossRefGoogle Scholar
Dunnage, J. E. A. (1972), ‘The number of real zeros of a class of random algebraic polynomial III’, J. London Math. Soc. (2) 6, 143–152.CrossRefGoogle Scholar