Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-03T16:43:27.341Z Has data issue: false hasContentIssue false
  • English
  • Français

LYAPUNOV-TYPE INEQUALITY FOR EXTREMAL PUCCI’S EQUATIONS

Part of: Elliptic equations and systems Representations of solutions

Published online by Cambridge University Press:  29 January 2020

J. TYAGI Open the ORCID record for J. TYAGI [Opens in a new window]  and
R. B. VERMA
J. TYAGI*
Affiliation:
Discipline of Mathematics, IIT Gandhinagar, Palaj, Gandhinagar 382355, India e-mail: jtyagi@iitgn.ac.in
R. B. VERMA
Affiliation:
Discipline of Mathematics, IIT Gandhinagar, Palaj, Gandhinagar 382355, India e-mail: rambv88@gmail.com
*
e-mail: jtyagi1@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we establish a Lyapunov-type inequality for the following extremal Pucci’s equation: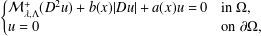

$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}{\mathcal{M}}_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D6EC}}^{+}(D^{2}u)+b(x)|Du|+a(x)u=0 & \text{in}~\unicode[STIX]{x1D6FA},\\ u=0 & \text{on}~\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA},\end{array}\right.\end{eqnarray}$$
where $\unicode[STIX]{x1D6FA}$ is a smooth bounded domain in 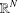$\mathbb{R}^{N}$, 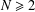$N\geq 2$. This work generalizes the well-known works on the Lyapunov inequality for extremal Pucci’s equations with gradient nonlinearity.

Keywords

35D40Pucci’s extremal operatornontrivial solutionsLyapunov inequalityviscosity solutions

MSC classification

Primary: 35J60: Nonlinear elliptic equations 35D40: Viscosity solutions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 109 , Issue 3 , December 2020 , pp. 416 - 430
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by J. McCoy

References

Athanassov, Z. S., ‘Total stability of sets for nonautonomous differential systems’, Trans. Amer. Math. Soc. 295(2) (1986), 649–663.Google Scholar
Borg, G., ‘On a Liapunoff criterion of stability’, Amer. J. Math. 71 (1949), 67–70.CrossRefGoogle Scholar
Brown, R. C. and Hilton, D. B., ‘Lyapunov inequalities and their applications’, in: Survey on Classical Inequalities, Mathematics and its Applications, 517 (Kluwer Academic, Dordrecht, 2010), 1–25.Google Scholar
Caffarelli, L. A., ‘Interior a priori estimates for solutions of fully non-linear equations’, Ann. Math. 130(1) (1989), 189–213.CrossRefGoogle Scholar
Cañada, A., Montero, J. A. and Villegas, S., ‘Lyapunov type inequalities and applications to PDE’, in: Elliptic and Parabolic Problems, Progress in Nonlinear Differential Equations and Their Applications, 63 (Birkhäuser, Basel, 2005), 103–110.Google Scholar
Cañada, A., Montero, J. A. and Villegas, S., ‘Liapunov type inequalities and Neumann boundary value problems at resonance’, Math. Inequal. Appl. 8(3) (2005), 459–475.Google Scholar
Cañada, A., Montero, J. A. and Villegas, S., ‘Lyapunov inequalities for partial differential equations’, J. Funct. Anal. 237 (2006), 176–193.CrossRefGoogle Scholar
Cañada, A. and Villegas, S., A Variational Approach to Lyapunov Type Inequalities from ODE to PDE, Springer Briefs in Mathematics (Springer, New York, 2015).CrossRefGoogle Scholar
Crandall, M. G., Caffarelli, L., Kocan, M. and Świech, A., ‘On viscosity solutions of fully nonlinear equations with measurable ingredients’, Comm. Pure Appl. Math. 49(4) (1996), 365–398.Google Scholar
Cutri, A. and Leoni, F., ‘On the Liouville property for fully nonlinear equations’, Ann. Inst. H. Poincaré Anal. Non Linéaire 17(2) (2000), 219–245.Google Scholar
De Nápoli, P. L. and Pinasco, J. P., ‘A Lyapunov inequality for monotone quasilinear operators’, Differential Integral Equations 18(10) (2005), 1193–1200.Google Scholar
De Nápoli, P. L. and Pinasco, J. P., ‘Lyapunov inequalities for partial differential equations’, J. Funct. Anal. 270(6) (2016), 1995–2018.Google Scholar
Elbert, A., ‘A half-linear second order differential equation’, Colloq. Math. Soc. Janos Bolyai 30 (1979), 158–180.Google Scholar
Ferreira, R. A. C., ‘A Lyapunov-type inequality for a fractional boundary value problem’, Fract. Calc. Appl. Anal. 16(4) (2013), 978–984.CrossRefGoogle Scholar
Ferreira, R. A. C., ‘On a Lyapunov-type inequality and the zeros of a certain Mittag–Leffler function’, J. Math. Anal. Appl. 412(2) (2014), 1058–1063.CrossRefGoogle Scholar
Fok, K., ‘A nonlinear Fabes–Stroock result’, Comm. Partial Differential Equations 23(5–6) (1998), 967–983.CrossRefGoogle Scholar
Hartman, P., Ordinary Differential Equations (Wiley, New York–London–Sydney, 1964).Google Scholar
Hashizume, M., ‘Minimization problem related to a Lyapunov inequality’, J. Math. Anal. Appl. 432(1) (2015), 517–530.CrossRefGoogle Scholar
Hashizume, M. and Takahashi, F., ‘Lyapunov inequality for an elliptic problem with the Robin boundary condition’, Nonlinear Anal. Theory Methods Appl. 129 (2015), 189–197.CrossRefGoogle Scholar
Jleli, M., Kirane, M. and Samet, B., ‘Lyapunov-type inequalities for fractional partial differential equations’, Appl. Math. Lett. 66(88) (2017), 30–39.CrossRefGoogle Scholar
Jleli, M. and Samet, B., ‘Lyapunov-type inequalities for a fractional differential equation with mixed boundary conditions’, Math. Inequal. Appl. 18(2) (2015), 443–451.Google Scholar
Jleli, M. and Samet, B., ‘Lyapunov-type inequalities for fractional boundary-value problems’, Electron. J. Differential Equations 88 (2015), 1–11.Google Scholar
Koike, S. and Świech, A., ‘Maximum principle for fully nonlinear equations via the iterated comparison function method’, Math. Ann. 339(2) (2007), 461–484.CrossRefGoogle Scholar
Lee, C.-F., Yeh, C.-C., Hong, C.-H. and Agarwal, R. P., ‘Lyapunov and Wirtinger inequalities’, Appl. Math. Lett. 17(7) (2004), 847–853.CrossRefGoogle Scholar
Liapunov, A. M., ‘Problème général de la stabilité du mouvement’, Ann. of Math. Stud. 17 (1947), 203–474.Google Scholar
Pinasco, J. P., ‘Lower bounds for eigenvalues of the one-dimensional p-Laplacian’, Abstr. Appl. Anal. 2 (2004), 147–153.CrossRefGoogle Scholar
Pinasco, J. P., Lyapunov-type Inequalities with Applications to Eigenvalue Problems, Springer Briefs in Mathematics (Springer, New York, 2013).CrossRefGoogle Scholar
Rong, J. and Bai, C., ‘Lyapunov-type inequality for a fractional differential equation with fractional boundary conditions’, Adv. Difference Equ. 82 (2015), 1–10.Google Scholar
Sànchez, J. and Vergara, V., ‘A Lyapunov-type inequality for a 𝛹-Laplacian operator’, Nonlinear Anal. Theory Methods Appl. 74 (2011), 7071–7077.CrossRefGoogle Scholar
Sirakov, B., ‘Solvability of uniformly elliptic fully nonlinear PDE’, Arch. Ration. Mech. Anal. 195(2) (2010), 579–607.CrossRefGoogle Scholar
Timoshin, S. A., ‘Lyapunov inequality for elliptic equations involving limiting nonlinearities’, Proc. Japan Acad. Ser. A Math. Sci. 86(8) (2010), 139–142.CrossRefGoogle Scholar
Tyagi, J. and Verma, R. B., ‘A survey on the existence, uniqueness and regularity questions to fully nonlinear elliptic partial differential equations’, Differ. Equ. Appl. 8(2) (2016), 135–205.Google Scholar
Tyagi, J. and Verma, R. B., ‘Positive solution of extremal Puccis equations with singular and sublinear nonlinearity’, Mediterr. J. Math. 14(4) Art. 148 (2017), 17 pp.Google Scholar
Tyagi, J. and Verma, R. B., ‘Positive solution to Pucci’s extremal equations with singular and gradient nonlinearity’, Discrete Contin. Dyn. Syst. A 39(5) (2019), 2637–2659.CrossRefGoogle Scholar
Wintner, A., ‘On the non-existence of conjugate points’, Amer. J. Math. 73 (1951), 368–380.CrossRefGoogle Scholar