Let M be an n-dimensional (n = 2m + 1, m ≦ 1) real differentiable manifold. if on M there exist a tensor field 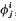, a contravariant vector field ξi and a convariant vector field ηi such that 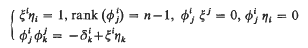then M is said to have an almost contact structure with the structure tensors (φ,ξ, η) [1], [2]. Further, if a positive definite Riemannian metric g satisfies the conditions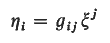 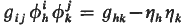then g is called an associated Riemannian metric to the almost contact structure and M is then said to have an almost contact metric structure. On the other hand, M is said to have a contact structure [2], [4] if there exists a 1-form η over M such that η ∧ (dη)m ≠ 0 everywhere over M where dη means the exterior derivation of η and the symbol ∧ means the exterior multiplication. In this case M is said to be a contact manifold with contact form η. It is known [2, Th. 3,1] that if η = ηidxi is a 1-form defining a contact structure, then there exists a positive definite Riemannian metric in gij such that 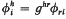and 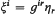define an almost contact metric structure with and ηi where 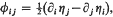the symbol ∂i standing for ∂/∂xi.