Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zeleznekow, John
1981.
Regular semirings.
Semigroup Forum,
Vol. 23,
Issue. 1,
p.
119.
Zeleznikow, John
1981.
Algebra Carbondale 1980.
Vol. 848,
Issue. ,
p.
255.
Batbedat, Andre
1984.
Algebras, prerings, semirings and rectangular bands.
Semigroup Forum,
Vol. 30,
Issue. 1,
p.
231.
McAlister, D.B
1984.
Rees matrix covers for regular semigroups.
Journal of Algebra,
Vol. 89,
Issue. 2,
p.
264.
Ponizovskiî, J. S.
1987.
Semigroup rings.
Semigroup Forum,
Vol. 36,
Issue. 1,
p.
1.
Ahsan, J.
Latif, R.
and
Shabir, M.
1993.
Representations of weakly regular semirings by sections in a presheaf.
Communications in Algebra,
Vol. 21,
Issue. 8,
p.
2819.
Hebisch, Udo
and
Weinert, Hanns Joachim
1996.
Vol. 1,
Issue. ,
p.
425.
Loyola, Jean Oesmer
1997.
E-free objects inE-varieties of inverse rings.
Semigroup Forum,
Vol. 54,
Issue. 1,
p.
375.
Ahsan, Javed
Shabir, M.
and
Weinert, H.J.
1998.
Characterizations of semirings byp-injective and projective semimodules.
Communications in Algebra,
Vol. 26,
Issue. 7,
p.
2199.
Yu, Jianping
Sun, Yongli
Li, Shizheng
and
Zhang, Yufen
2010.
Structure of Completely π-Inverse Semirings.
Algebra Colloquium,
Vol. 17,
Issue. 01,
p.
101.
SHAO, YONG
CRVENKOVIĆ, SINIŠA
and
MITROVIĆ, MELANIJA
2013.
THE ZELEZNIKOW PROBLEM ON A CLASS OF ADDITIVELY IDEMPOTENT SEMIRINGS.
Journal of the Australian Mathematical Society,
Vol. 95,
Issue. 3,
p.
404.
Abawajy, J.
Kelarev, A. V.
and
Zeleznikow, J.
2013.
Centroid sets with largest weight in Munn semirings for data mining applications.
Semigroup Forum,
Vol. 87,
Issue. 3,
p.
617.
Huang, Kaiqing
Chen, Yizhi
and
Gan, Aiping
2022.
Structure of split additively orthodox semirings.
AIMS Mathematics,
Vol. 7,
Issue. 6,
p.
11345.




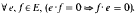 (ii) (
(ii) (