Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-01T02:06:44.940Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME GLOBAL EXISTENCE RESULTS ON LOCALLY FINITE GRAPHS

Part of: Miscellaneous topics - Partial differential equations Partial differential equations

Published online by Cambridge University Press:  06 November 2023

SHOUDONG MAN Open the ORCID record for SHOUDONG MAN [Opens in a new window]  and
GUOQING ZHANG Open the ORCID record for GUOQING ZHANG [Opens in a new window]
SHOUDONG MAN*
Affiliation:
College of Science and Technology, Tianjin University of Finance and Economics, Zhujiang Road, Tianjin 300222, PR China
GUOQING ZHANG
Affiliation:
College of Science, University of Shanghai for Science and Technology, Jungong Road, Shanghai 200093, PR China e-mail: shzhangguoqing@126.com
*
e-mail: shoudongmantj@tjufe.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 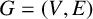$G=(V, E)$ be a locally finite graph with the vertex set V and the edge set E, where both V and E are infinite sets. By dividing the graph G into a sequence of finite subgraphs, the existence of a sequence of local solutions to several equations involving the p-Laplacian and the poly-Laplacian systems is confirmed on each subgraph, and the global existence for each equation on graph G is derived by the convergence of these local solutions. Such results extend the recent work of Grigor’yan, Lin and Yang [J. Differential Equations, 261 (2016), 4924–4943; Rev. Mat. Complut., 35 (2022), 791–813]. The method in this paper also provides an idea for investigating similar problems on infinite graphs.

Keywords

analysis on graphSobolev embedding theoremdivision of a graphexistence of global solution

MSC classification

Primary: 35R02: Partial differential equations on graphs and networks (ramified or polygonal spaces)
Secondary: 35A01: Existence problems
Type
Research Article
Information
Journal of the Australian Mathematical Society , First View , pp. 1 - 17
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Florica C. Cîrstea

The first author was supported by the National Natural Science Foundation of China (Grant No. 11601368). The second author was supported by Shanghai Natural Science Foundation (Grant No. 21ZR1445600)

References

Che, G., Chen, C. and Shi, H., ‘Ground state of semilinear elliptic systems with sum of periodic and Hardy potentials’, Complex Var. Elliptic Equ. 65(2020), 381–408.10.1080/17476933.2019.1584194CrossRefGoogle Scholar
Corra Corrêa, F. J. S. A., dos Santos, G. C. G., Tavares, L. S. and Muhassua, S. S., ‘Existence of solution for a singular elliptic system with convection terms’, Nonlinear Anal. Real World Appl. 66 (2022), 103549.CrossRefGoogle Scholar
Ge, H., ‘A $p$ -th Yamabe equation on graph’, Proc. Amer. Math. Soc. 146 (2018), 2219–2224.10.1090/proc/13929CrossRefGoogle Scholar
Grigor’yan, A., Lin, Y. and Yang, Y., ‘Yamabe type equations on graphs’, J. Differential Equations 261 (2016), 4924–4943.CrossRefGoogle Scholar
Grigor’yan, A., Lin, Y. and Yang, Y., ‘Kazdan–Warner equation on graph’, Calc. Var. Partial Differential Equations 55 (2016), 92–113.10.1007/s00526-016-1042-3CrossRefGoogle Scholar
Grigor’yan, A., Lin, Y. and Yang, Y., ‘Existence of positive solutions to some nonlinear equations on locally finite graphs’, Sci. China Math. 60 (2017), 1311–1324.CrossRefGoogle Scholar
Hua, B. and Keller, M., ‘Harmonic functions of general graph Laplacians’, Calc. Var. Partial Differential Equations 51 (2014), 343–362.10.1007/s00526-013-0677-6CrossRefGoogle Scholar
Kang, J. H. and Robertson, T., ‘An elliptic nonlinear system of multiple functions with application’, Dyn. Partial Differ. Equ. 19 (2022), 141–162.10.4310/DPDE.2022.v19.n2.a3CrossRefGoogle Scholar
Lin, Y., Ngai, S.-M. and Yau, S.-T., ‘Heat kernels on forms defined on a subgraph of a complete graph’, Math. Ann. 380 (2021), 1891–1931.CrossRefGoogle Scholar
Lin, Y. and Wu, Y., ‘The existence and nonexistence of global solutions for a semilinear heat equation on graphs’, Calc. Var. Partial Differential Equations 56 (2017), 102.CrossRefGoogle Scholar
Lin, Y. and Yang, Y., ‘Calculus of variations on locally finite graphs’, Rev. Mat. Complut. 35 (2022), 791–813.10.1007/s13163-021-00405-yCrossRefGoogle Scholar
Yang, Y., ‘Existence of positive solutions to quasi-linear elliptic equations with exponential growth in the whole Euclidean space’, J. Funct. Anal. 262 (2012), 1679–1704.CrossRefGoogle Scholar