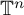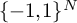1 Introduction
Let
![]() $\mathbb { T}$
be the torus in the complex plane, that is, the compact abelian group of all
$\mathbb { T}$
be the torus in the complex plane, that is, the compact abelian group of all
![]() $z \in \mathbb {C}$
with
$z \in \mathbb {C}$
with
![]() $|z|=1$
, which carries the normalised Lebesgue measure
$|z|=1$
, which carries the normalised Lebesgue measure
![]() $\nu $
on
$\nu $
on
![]() $\mathbb { T}$
as its Haar measure. By
$\mathbb { T}$
as its Haar measure. By
![]() $\mathbb { T}^\infty $
, we denote the countable product of
$\mathbb { T}^\infty $
, we denote the countable product of
![]() $\mathbb { T}$
, which, again, forms a compact abelian group (the Haar measure is the countable product of
$\mathbb { T}$
, which, again, forms a compact abelian group (the Haar measure is the countable product of
![]() $\nu $
), and identify its dual group with
$\nu $
), and identify its dual group with
![]() $\mathbb {Z}^{(\mathbb {N})}$
, all finite multi indices
$\mathbb {Z}^{(\mathbb {N})}$
, all finite multi indices
![]() $\alpha \in \mathbb {Z}^n,\,n \in \mathbb {N}$
. We write
$\alpha \in \mathbb {Z}^n,\,n \in \mathbb {N}$
. We write
![]() $\mathbb {N}_0^{(\mathbb {N})}$
for all
$\mathbb {N}_0^{(\mathbb {N})}$
for all
![]() $\alpha \in \mathbb {Z}^{(\mathbb {N})}$
with entries in
$\alpha \in \mathbb {Z}^{(\mathbb {N})}$
with entries in
![]() $\mathbb { N}_0:=\mathbb {N} \cup \{ 0\}$
.
$\mathbb { N}_0:=\mathbb {N} \cup \{ 0\}$
.
As usual,
![]() $H_\infty (\mathbb { T}^\infty )$
stands for the Banach space of all functions
$H_\infty (\mathbb { T}^\infty )$
stands for the Banach space of all functions
![]() $f \in L_\infty (\mathbb { T}^\infty )$
, such that
$f \in L_\infty (\mathbb { T}^\infty )$
, such that
![]() $\widehat {f}(\alpha )= 0$
for all
$\widehat {f}(\alpha )= 0$
for all
![]() $\alpha =(\alpha _i) \in \mathbb {Z}^{(\mathbb {N})}$
with
$\alpha =(\alpha _i) \in \mathbb {Z}^{(\mathbb {N})}$
with
![]() $\alpha _j<0$
for some j. We call
$\alpha _j<0$
for some j. We call
![]() $H_\infty (\mathbb { T}^\infty )$
Hardy space on the infinite dimensional torus and denote its closed subspace of all continuous functions by
$H_\infty (\mathbb { T}^\infty )$
Hardy space on the infinite dimensional torus and denote its closed subspace of all continuous functions by
![]() $C^A(\mathbb { T}^\infty )$
.
$C^A(\mathbb { T}^\infty )$
.
A sequence
![]() $\xi = (\xi _\alpha )_{\alpha \in \mathbb {N}_0^{(\mathbb {N})}} $
of scalars is a bounded
$\xi = (\xi _\alpha )_{\alpha \in \mathbb {N}_0^{(\mathbb {N})}} $
of scalars is a bounded
![]() $\ell _1(\mathbb {N}_0^{(\mathbb {N})})$
-multiplier of
$\ell _1(\mathbb {N}_0^{(\mathbb {N})})$
-multiplier of
![]() $C^A(\mathbb {T}^\infty )$
, whenever the mapping
$C^A(\mathbb {T}^\infty )$
, whenever the mapping
![]() $ M_\xi \colon C^{A}(\mathbb {T}^\infty ) \to \ell _1(\mathbb {N}_0^{(\mathbb {N})})$
given by:
$ M_\xi \colon C^{A}(\mathbb {T}^\infty ) \to \ell _1(\mathbb {N}_0^{(\mathbb {N})})$
given by:
is bounded. The following necessary condition for such multipliers is due to Kislyakov [Reference Kislyakov15, Theorem 6], and it, in fact, is the main motivation of this paper.
Theorem 1.1. Let
![]() $\xi = (\xi _\alpha )_{\alpha \in \mathbb {N}_0^{(\mathbb {N})}} $
be a bounded
$\xi = (\xi _\alpha )_{\alpha \in \mathbb {N}_0^{(\mathbb {N})}} $
be a bounded
![]() $\ell _1(\mathbb {N}_0^{(\mathbb {N})})$
-multiplier of
$\ell _1(\mathbb {N}_0^{(\mathbb {N})})$
-multiplier of
![]() $C^A(\mathbb {T}^\infty )$
. Then:
$C^A(\mathbb {T}^\infty )$
. Then:
 $$ \begin{align} \sup_{n,d \in \mathbb{ N}}\,\,\,\frac{1}{\sqrt{n \log( 1+dn)}} \Big(\sum_{\alpha \in \mathbb{N}_0^n \colon \max\{\alpha_1,\ldots,\alpha_n\}\leq d} & |\xi_{\alpha}|^2\Big)^{1/2} \,\,\,< \infty. \end{align} $$
$$ \begin{align} \sup_{n,d \in \mathbb{ N}}\,\,\,\frac{1}{\sqrt{n \log( 1+dn)}} \Big(\sum_{\alpha \in \mathbb{N}_0^n \colon \max\{\alpha_1,\ldots,\alpha_n\}\leq d} & |\xi_{\alpha}|^2\Big)^{1/2} \,\,\,< \infty. \end{align} $$
Inspired by this result, in particular, the techniques from local Banach space theory which Kislyakov uses to prove it, we study the following more general (but also more vague) question:
Let G be a compact abelian group with Haar measure
![]() $\nu $
and
$\nu $
and
![]() $\Gamma $
a subset of characters in the dual group
$\Gamma $
a subset of characters in the dual group
![]() $\widehat {G}$
. Moreover, let
$\widehat {G}$
. Moreover, let
![]() $X(\Gamma )$
be a Banach sequence space over the set
$X(\Gamma )$
be a Banach sequence space over the set
![]() $\Gamma $
. A (real or complex) sequence
$\Gamma $
. A (real or complex) sequence
![]() $\xi = (\xi _\gamma )_{\gamma \in \Gamma }$
is an
$\xi = (\xi _\gamma )_{\gamma \in \Gamma }$
is an
![]() $X(\Gamma )$
-multiplier of a closed subspace
$X(\Gamma )$
-multiplier of a closed subspace
![]() $V \subset L_p(G)$
whenever:
$V \subset L_p(G)$
whenever:
The problem then is to find necessary and sufficient conditions for such
![]() $X(\Gamma )$
-multipliers of V. Our applications mainly focus on multiplier theorems for the n-dimensional torus
$X(\Gamma )$
-multipliers of V. Our applications mainly focus on multiplier theorems for the n-dimensional torus
![]() $\mathbb {T}^n$
, its Boolean counterpart, the n-dimensional Boolean cube
$\mathbb {T}^n$
, its Boolean counterpart, the n-dimensional Boolean cube
![]() $\{-1,1\}^n$
, as well as their countable counterparts
$\{-1,1\}^n$
, as well as their countable counterparts
![]() $\mathbb {T}^\infty := \mathbb {T}^{\mathbb {N}}$
and
$\mathbb {T}^\infty := \mathbb {T}^{\mathbb {N}}$
and
![]() $\{-1,1\}^\infty := \{-1, 1\}^{\mathbb {N}}$
.
$\{-1,1\}^\infty := \{-1, 1\}^{\mathbb {N}}$
.
Observe that by a simple closed graph argument, the study of
![]() $X(\Gamma )$
-multipliers for
$X(\Gamma )$
-multipliers for
![]() $V \subset L_\infty (G)$
means to study concrete inequalities:
$V \subset L_\infty (G)$
means to study concrete inequalities:
![]() $\xi $
is an
$\xi $
is an
![]() $X(\Gamma )$
-multiplier for
$X(\Gamma )$
-multiplier for
![]() $V \subset L_\infty (G)$
if and only if there is a constant
$V \subset L_\infty (G)$
if and only if there is a constant
![]() $C=C(\xi )~>~0$
, such that:
$C=C(\xi )~>~0$
, such that:
 $$\begin{align*}\sum_{\gamma \in \Gamma} |\widehat{f}(\gamma) \xi_\gamma|\leq C \|f\|_\infty, \quad\, f\in V. \end{align*}$$
$$\begin{align*}\sum_{\gamma \in \Gamma} |\widehat{f}(\gamma) \xi_\gamma|\leq C \|f\|_\infty, \quad\, f\in V. \end{align*}$$
We note that, only in very few cases, a full description of the set of all X-multipliers
![]() $\xi $
of
$\xi $
of
![]() $V \subset L_\infty (G)$
is possible. In most of our applications, we are able to give necessary and/or sufficient conditions in terms of the asymptotic decay of
$V \subset L_\infty (G)$
is possible. In most of our applications, we are able to give necessary and/or sufficient conditions in terms of the asymptotic decay of
![]() $\xi $
.
$\xi $
.
In the first section, we show that Theorem 1.1 is in fact a consequence of the Kahane–Salem–Zygmund inequality, and in Theorem 3.2 and Corollary 3.3, we extend Kislyakov’s multiplier theorem to certain analytic subspaces of
![]() $L_\infty (\mathbb {T}^\infty )$
instead of
$L_\infty (\mathbb {T}^\infty )$
instead of
![]() $C^A(\mathbb { T}^\infty )$
. It should be mentioned here that Kislyakov’s approach to Theorem 1.1 is different, and in the second and third sections, we analyse his cycle of ideas from local Banach space theory — the main advantage is that they apply to more general compact abelian groups than only multidimensional tori.
$C^A(\mathbb { T}^\infty )$
. It should be mentioned here that Kislyakov’s approach to Theorem 1.1 is different, and in the second and third sections, we analyse his cycle of ideas from local Banach space theory — the main advantage is that they apply to more general compact abelian groups than only multidimensional tori.
The crucial link, which makes this possible, comes from Lemma 4.1 showing that, given a compact abelian group G, a finite subset
![]() $\Gamma $
in
$\Gamma $
in
![]() $\widehat {G}$
and a Banach space
$\widehat {G}$
and a Banach space
![]() $F:=(\mathbb {C}^{\Gamma }, \|\cdot \|)$
, for every finite sequence
$F:=(\mathbb {C}^{\Gamma }, \|\cdot \|)$
, for every finite sequence
![]() $\xi = (\xi _\gamma )_{\gamma \in \Gamma }$
, one has:
$\xi = (\xi _\gamma )_{\gamma \in \Gamma }$
, one has:
where
![]() $\mathcal P_\Gamma $
stands for the Banach space of all finite polynomials
$\mathcal P_\Gamma $
stands for the Banach space of all finite polynomials
![]() $\sum _{\gamma \in \Gamma }\xi _\gamma \gamma $
endowed with the sup norm,
$\sum _{\gamma \in \Gamma }\xi _\gamma \gamma $
endowed with the sup norm,
![]() $M_\xi $
for the multiplier, which assigns to every finite polynomial
$M_\xi $
for the multiplier, which assigns to every finite polynomial
![]() $\sum _{\gamma \in \Gamma }\mu _\gamma \gamma $
, the finite sequence
$\sum _{\gamma \in \Gamma }\mu _\gamma \gamma $
, the finite sequence
![]() $(\mu _{\gamma } \xi _\gamma )_{\gamma \in \Gamma } \in F$
and
$(\mu _{\gamma } \xi _\gamma )_{\gamma \in \Gamma } \in F$
and
![]() $\pi _2(M_\xi )$
for the
$\pi _2(M_\xi )$
for the
![]() $2$
-summing norm of this operator.
$2$
-summing norm of this operator.
In the Theorems 4.4, 5.2 and 5.5, fundamental knowledge on
![]() $2$
-summing operators leads to improvements of Theorem 1.1.
$2$
-summing operators leads to improvements of Theorem 1.1.
In the last section, we apply our results to study multiplier theorems for spaces of functions on multidimensional tori and Boolean cubes. We focus on topics like Sidon constants, Bohr radii, monomial convergence, as well as Dirichlet series.
Using Kislyakov’s ideas, we prove new results, but we also reprove recent known results, which were originally proved through the use of the Kahane–Salem–Zygmund inequality.
At first glance, this might look surprising, but on the other hand, we already remarked that our starting point, Theorem 1.1, is a consequence of the Kahane–Salem–Zygmund inequality, and, conversely, we show in the recent paper [Reference Defant and Mastyło10] that Kislyakov’s ideas are of great relevance within a further study of the Kahane–Salem–Zygmund inequality.
2 Preliminaries
Banach spaces. Let X, Y be Banach spaces. We denote by
![]() $B_X$
the closed unit ball of X and by
$B_X$
the closed unit ball of X and by
![]() $X^{*}$
its dual Banach space. If we write
$X^{*}$
its dual Banach space. If we write
![]() $X\hookrightarrow Y$
, then we assume that
$X\hookrightarrow Y$
, then we assume that
![]() $X\subset Y$
and the inclusion map
$X\subset Y$
and the inclusion map
![]() $\mathrm {{id}}\colon X \to Y$
is bounded. If
$\mathrm {{id}}\colon X \to Y$
is bounded. If
![]() $X=Y$
with equality of norms, then we write
$X=Y$
with equality of norms, then we write
![]() $X\cong Y$
. As usual,
$X\cong Y$
. As usual,
![]() $C(K)$
denotes the Banach space of all continuous functions on a compact Hausdorff space K, with the sup norm
$C(K)$
denotes the Banach space of all continuous functions on a compact Hausdorff space K, with the sup norm
![]() $\|\cdot \|_\infty $
.
$\|\cdot \|_\infty $
.
We denote by
![]() $L(X, Y)$
the space of all bounded linear operators
$L(X, Y)$
the space of all bounded linear operators
![]() $T \colon X\to Y$
with the usual operator norm. An operator
$T \colon X\to Y$
with the usual operator norm. An operator
![]() $T \in L(X, Y)$
is said to be an isomorphic embedding of X into Y whenever there exists
$T \in L(X, Y)$
is said to be an isomorphic embedding of X into Y whenever there exists
![]() $C>0$
, such that
$C>0$
, such that
![]() $\|Tx\|_Y \geq C \|x\|_X$
for every
$\|Tx\|_Y \geq C \|x\|_X$
for every
![]() $x\in X$
. Thus,
$x\in X$
. Thus,
![]() $T^{-1}$
is an isomorphism from
$T^{-1}$
is an isomorphism from
![]() $(TX, \|\cdot \|_Y)$
onto X. Given a real number
$(TX, \|\cdot \|_Y)$
onto X. Given a real number
![]() $1\leq \lambda <\infty $
, we say that
$1\leq \lambda <\infty $
, we say that
![]() $X \lambda $
-embeds into Y whenever there exists an isomorphic embedding T of X into Y, such that
$X \lambda $
-embeds into Y whenever there exists an isomorphic embedding T of X into Y, such that
![]() $\|T\|\,\|T^{-1}\| \leq \lambda $
. In this case, we call T a
$\|T\|\,\|T^{-1}\| \leq \lambda $
. In this case, we call T a
![]() $\lambda $
-embedding of X into Y.
$\lambda $
-embedding of X into Y.
Let
![]() $\Gamma $
be a nonempty set. We denote by
$\Gamma $
be a nonempty set. We denote by
![]() $\ell _\infty (\Gamma )$
the space of all bounded functions on
$\ell _\infty (\Gamma )$
the space of all bounded functions on
![]() $\Gamma $
, endowed with the sup norm. For any
$\Gamma $
, endowed with the sup norm. For any
![]() $\xi , \eta \in \ell _{\infty }(\Gamma )$
, we denote by
$\xi , \eta \in \ell _{\infty }(\Gamma )$
, we denote by
![]() $\xi \cdot \eta $
their pointwise product. Let E and F be linear subspaces of
$\xi \cdot \eta $
their pointwise product. Let E and F be linear subspaces of
![]() $\mathbb {K}^{\Gamma }$
, where
$\mathbb {K}^{\Gamma }$
, where
![]() $\mathbb {K} = \mathbb {R}$
or
$\mathbb {K} = \mathbb {R}$
or
![]() $\mathbb {K} = \mathbb {C}$
. Any
$\mathbb {K} = \mathbb {C}$
. Any
![]() $\xi \in \mathbb {K}^\Gamma $
, such that
$\xi \in \mathbb {K}^\Gamma $
, such that
![]() $\xi \eta :=\xi \cdot \eta \in F$
for all
$\xi \eta :=\xi \cdot \eta \in F$
for all
![]() $\eta \in E$
, defines a diagonal operator
$\eta \in E$
, defines a diagonal operator
![]() $D_\xi \colon E \to F$
given by
$D_\xi \colon E \to F$
given by
![]() $D_\xi (\eta ):= \xi \eta $
for all
$D_\xi (\eta ):= \xi \eta $
for all
![]() $\eta \in E$
. We write
$\eta \in E$
. We write
![]() $\mathcal {D}(E,F)$
for the vector space of all such maps. If E and F are Banach spaces, such that the inclusion maps from E and F into
$\mathcal {D}(E,F)$
for the vector space of all such maps. If E and F are Banach spaces, such that the inclusion maps from E and F into
![]() $\mathbb {K}^{\Gamma }$
are continuous, then
$\mathbb {K}^{\Gamma }$
are continuous, then
![]() $\mathcal {D}(E, F)$
equipped with the norm:
$\mathcal {D}(E, F)$
equipped with the norm:
is a Banach space.
We apply standard methods from local Banach space theory. Recall that a Banach space X has cotype
![]() $2$
whenever there is a constant C, such that for each choice of finitely many
$2$
whenever there is a constant C, such that for each choice of finitely many
![]() $x_1, \ldots ,x_n \in X$
:
$x_1, \ldots ,x_n \in X$
:
 $$\begin{align*}\Big(\sum_{k=1}^n \|x_k\|^2 \Big)^{\frac{1}{2}} \leq C \Big(\int_0^1\Big\|\sum_{k=1}^n r_k(t) x_k \Big\|^2 dt\Big)^{\frac{1}{2}}, \end{align*}$$
$$\begin{align*}\Big(\sum_{k=1}^n \|x_k\|^2 \Big)^{\frac{1}{2}} \leq C \Big(\int_0^1\Big\|\sum_{k=1}^n r_k(t) x_k \Big\|^2 dt\Big)^{\frac{1}{2}}, \end{align*}$$
where
![]() $r_k$
denotes the kth Rademacher function. The least possible value of this constant is denoted
$r_k$
denotes the kth Rademacher function. The least possible value of this constant is denoted
![]() $C_2(X)$
.
$C_2(X)$
.
An operator
![]() $T\colon X\to Y$
between Banach spaces is said to be absolutely p-summing (p-summing for short) with
$T\colon X\to Y$
between Banach spaces is said to be absolutely p-summing (p-summing for short) with
![]() $1\leq p<\infty $
if there is a constant
$1\leq p<\infty $
if there is a constant
![]() $C>0$
, such that, for each
$C>0$
, such that, for each
![]() $n\in \mathbb {N}$
and for all sequences
$n\in \mathbb {N}$
and for all sequences
![]() $(x_k)_{k=1}^n$
in X, we have:
$(x_k)_{k=1}^n$
in X, we have:
 $$\begin{align*}\Big(\sum_{k=1}^n \|Tx_k\|_{Y}^p\Big)^{1/p} \leq C \sup_{x^{*}\in B_{X^{*}}} \Big(\sum_{k=1}^n |x^{*}(x_k)|^p\Big)^{\frac{1}{p}}. \end{align*}$$
$$\begin{align*}\Big(\sum_{k=1}^n \|Tx_k\|_{Y}^p\Big)^{1/p} \leq C \sup_{x^{*}\in B_{X^{*}}} \Big(\sum_{k=1}^n |x^{*}(x_k)|^p\Big)^{\frac{1}{p}}. \end{align*}$$
The least such constant C is denoted by
![]() $\pi _p(T\colon X \to Y)$
(
$\pi _p(T\colon X \to Y)$
(
![]() $\pi _p(T)$
for short) and is called the absolutely p-summing norm of T. We refer to the theory of p-summing operators to [Reference Diestel, Jarchow and Tonge13] and [Reference Pisier19].
$\pi _p(T)$
for short) and is called the absolutely p-summing norm of T. We refer to the theory of p-summing operators to [Reference Diestel, Jarchow and Tonge13] and [Reference Pisier19].
We recall that if K is a compact Hausdorff space, X a closed subspace of
![]() $C(K)$
and Y a Banach space, then the so-called Pietsch domination theorem states that
$C(K)$
and Y a Banach space, then the so-called Pietsch domination theorem states that
![]() $T\colon X\to Y$
is p-summing if and only if there is a constant C and a probability Borel measure
$T\colon X\to Y$
is p-summing if and only if there is a constant C and a probability Borel measure
![]() $\mu $
on K, such that:
$\mu $
on K, such that:
 $$\begin{align*}\|Tf\|_Y \leq C \Big(\int_K |f|^p\,d\mu \Big)^{\frac{1}{p}}, \quad\, f\in X. \end{align*}$$
$$\begin{align*}\|Tf\|_Y \leq C \Big(\int_K |f|^p\,d\mu \Big)^{\frac{1}{p}}, \quad\, f\in X. \end{align*}$$
In that case,
![]() $\pi _{p}(T)$
coincides with the smallest constant C satisfying the previous inequality.
$\pi _{p}(T)$
coincides with the smallest constant C satisfying the previous inequality.
Compact abelian groups. In the following, we fix some compact abelian group
![]() $G := (G, \cdot )$
. A linear subspace X of
$G := (G, \cdot )$
. A linear subspace X of
![]() $\mathbb {K}^{G}$
is said to be translation invariant whenever for every
$\mathbb {K}^{G}$
is said to be translation invariant whenever for every
![]() $f\in X$
and every
$f\in X$
and every
![]() $h\in G$
, the translation
$h\in G$
, the translation
![]() $f_h \in X$
, where
$f_h \in X$
, where
![]() $f_h(g):= f(g\cdot h)$
for every
$f_h(g):= f(g\cdot h)$
for every
![]() $g\in G$
.
$g\in G$
.
As usual, we write
![]() $\widehat {G}$
for the dual group of G (i.e. the set of all continuous characters on G), and we denote by
$\widehat {G}$
for the dual group of G (i.e. the set of all continuous characters on G), and we denote by
![]() $\nu $
the (normalised) Haar measure on G, a unique translation invariant regular Borel probability measure. Recall that the translation invariance of
$\nu $
the (normalised) Haar measure on G, a unique translation invariant regular Borel probability measure. Recall that the translation invariance of
![]() $\nu $
is equivalent to the formula:
$\nu $
is equivalent to the formula:
The following well-known result from [Reference Pełczyński18] is central for our purposes; for the sake of completeness, we include a simple proof.
Lemma 2.1. Let G be a compact abelian group with normalised Haar measure
![]() $\nu $
, let X be a closed translation invariant subspace of
$\nu $
, let X be a closed translation invariant subspace of
![]() $C(G)$
and let Y be an arbitrary Banach space. Suppose that
$C(G)$
and let Y be an arbitrary Banach space. Suppose that
![]() $T\colon X \to Y$
is a p-summing operator which satisfies that
$T\colon X \to Y$
is a p-summing operator which satisfies that
![]() $\|Tf_h\|_Y = \|Tf\|_Y$
for all
$\|Tf_h\|_Y = \|Tf\|_Y$
for all
![]() $f\in X$
,
$f\in X$
,
![]() $h\in G$
. Then:
$h\in G$
. Then:
 $$\begin{align*}\|Tf\|_Y \leq \pi_p(T)\Big(\int_G |f(g)|^p\,d\nu(g) \Big)^{1/p}, \quad\, f\in X. \end{align*}$$
$$\begin{align*}\|Tf\|_Y \leq \pi_p(T)\Big(\int_G |f(g)|^p\,d\nu(g) \Big)^{1/p}, \quad\, f\in X. \end{align*}$$
Proof. Pietsch’s domination theorem combined with Fubini’s theorem show that there is a probability Borel measure
![]() $\mu $
on G, such that for all
$\mu $
on G, such that for all
![]() $f\in X$
:
$f\in X$
:
 $$ \begin{align*} \|Tf\|_{Y}^{p} & = \int_G \|Tf_h\|_{Y}^p \,d\nu(h) \leq \pi_p(T)^p \int_G\Big(\int_G |f_h(g)|^p\,d\mu(g)\Big)\,d\nu(h) \\ & = \pi_p(T)^p \int_G\Big(\int_G |f_h(g)|^p\,d\nu(h) \Big)\,d\mu(g). \end{align*} $$
$$ \begin{align*} \|Tf\|_{Y}^{p} & = \int_G \|Tf_h\|_{Y}^p \,d\nu(h) \leq \pi_p(T)^p \int_G\Big(\int_G |f_h(g)|^p\,d\mu(g)\Big)\,d\nu(h) \\ & = \pi_p(T)^p \int_G\Big(\int_G |f_h(g)|^p\,d\nu(h) \Big)\,d\mu(g). \end{align*} $$
Since the Haar measure
![]() $\nu $
is translation invariant, it follows that:
$\nu $
is translation invariant, it follows that:
 $$ \begin{align*} \|Tf\|_{Y}^{p} & = \pi_p(T)^p \int_G\Big(\int_G |f_g(h)|^p\,d\nu(h) \Big)\,d\mu(g) \\ & = \pi_p(T)^p \int_G\Big(\int_G |f(h)|^p\,d\nu(h) \Big)\,d\mu(g) = \pi_p(T)^p \int_G |f(h)|^p\,d\nu(h). \\[-42pt] \end{align*} $$
$$ \begin{align*} \|Tf\|_{Y}^{p} & = \pi_p(T)^p \int_G\Big(\int_G |f_g(h)|^p\,d\nu(h) \Big)\,d\mu(g) \\ & = \pi_p(T)^p \int_G\Big(\int_G |f(h)|^p\,d\nu(h) \Big)\,d\mu(g) = \pi_p(T)^p \int_G |f(h)|^p\,d\nu(h). \\[-42pt] \end{align*} $$
As usual, the Fourier transform of
![]() $f\in L_1(G, \nu )$
is defined by:
$f\in L_1(G, \nu )$
is defined by:
Let X be any subspace of
![]() $L_1(G, \nu )$
and
$L_1(G, \nu )$
and
![]() $\Gamma \subset \widehat {G}$
a nonempty subset. Then:
$\Gamma \subset \widehat {G}$
a nonempty subset. Then:
Clearly,
![]() $X_\Gamma $
is a translation invariant subspace of X. Note that for
$X_\Gamma $
is a translation invariant subspace of X. Note that for
![]() $X=C(G)$
or
$X=C(G)$
or
![]() $X=L_p(G, \nu )$
with
$X=L_p(G, \nu )$
with
![]() $1\leq p<\infty $
, every translation invariant subspace of X has the form
$1\leq p<\infty $
, every translation invariant subspace of X has the form
![]() $X_\Gamma $
for some
$X_\Gamma $
for some
![]() $\Gamma \subset \widehat {G}$
.
$\Gamma \subset \widehat {G}$
.
In what follows, for simplicity of notation, we write
![]() $C_\Gamma $
instead of
$C_\Gamma $
instead of
![]() $C(G)_\Gamma $
. By
$C(G)_\Gamma $
. By
![]() $\widehat {C_\Gamma } \subset \mathbb {K}^\Gamma $
, we denote the linear space of all
$\widehat {C_\Gamma } \subset \mathbb {K}^\Gamma $
, we denote the linear space of all
![]() $(\widehat {f}(\gamma ))_{\gamma \in \Gamma }, \, f \in C_\Gamma $
, which equipped with the norm:
$(\widehat {f}(\gamma ))_{\gamma \in \Gamma }, \, f \in C_\Gamma $
, which equipped with the norm:
forms a Banach space. Throughout the paper, if
![]() $\xi \in \mathbb {K}^\Gamma $
and
$\xi \in \mathbb {K}^\Gamma $
and
![]() $F=(\mathbb {K}^\Gamma ,\|\cdot \|)$
are Banach spaces, then the mapping
$F=(\mathbb {K}^\Gamma ,\|\cdot \|)$
are Banach spaces, then the mapping
![]() $M_\xi \colon C_\Gamma \to F$
(which we call multiplier) is given by:
$M_\xi \colon C_\Gamma \to F$
(which we call multiplier) is given by:
The space of all such multipliers is denoted by
![]() $\mathcal {M}(C_\Gamma , F)$
, and it obviously identifies with the space
$\mathcal {M}(C_\Gamma , F)$
, and it obviously identifies with the space
![]() $\mathcal {D}(\widehat {C_\Gamma }, F)$
of all diagonal operators from
$\mathcal {D}(\widehat {C_\Gamma }, F)$
of all diagonal operators from
![]() $\widehat {C_\Gamma }$
into F.
$\widehat {C_\Gamma }$
into F.
A subset
![]() $\Gamma $
of
$\Gamma $
of
![]() $\widehat {G}$
is called a p-Sidon set (
$\widehat {G}$
is called a p-Sidon set (
![]() $1\leq p<\infty $
) if there is a constant C, such that:
$1\leq p<\infty $
) if there is a constant C, such that:
 $$\begin{align*}\Big(\sum_{\gamma \in \Gamma} |\widehat{f}(\gamma)|^p\Big)^{\frac{1}{p}} \leq C \|f\|_{\infty}, \quad\, f\in C_\Gamma. \end{align*}$$
$$\begin{align*}\Big(\sum_{\gamma \in \Gamma} |\widehat{f}(\gamma)|^p\Big)^{\frac{1}{p}} \leq C \|f\|_{\infty}, \quad\, f\in C_\Gamma. \end{align*}$$
The least possible value of this constant is denoted
![]() $S_p(\Gamma )$
and called the p-Sidon constant of G.
$S_p(\Gamma )$
and called the p-Sidon constant of G.
Let
![]() $\{-1,1\}$
be the compact discrete group with the Haar measure
$\{-1,1\}$
be the compact discrete group with the Haar measure
![]() $\sigma _{1}(\{-1\}) = \sigma _{1}(\{1\}) = 1/2$
, and let
$\sigma _{1}(\{-1\}) = \sigma _{1}(\{1\}) = 1/2$
, and let
![]() $\mathbb {T}$
be a unit circle equipped with normalised Lebesgue measure. We will primarily be interested in the case when
$\mathbb {T}$
be a unit circle equipped with normalised Lebesgue measure. We will primarily be interested in the case when
![]() $G=\mathbb {T}^n$
,
$G=\mathbb {T}^n$
,
![]() $G= \{-1, 1\}^{N}$
,
$G= \{-1, 1\}^{N}$
,
![]() $G=\{-1,1\}^{\infty }$
or
$G=\{-1,1\}^{\infty }$
or
![]() $G = \mathbb {T}^{\infty }$
.
$G = \mathbb {T}^{\infty }$
.
The countable product
![]() $\{-1,1\}^{\infty }$
is a compact abelian group with the pointwise product and the product topology. The Haar measure on
$\{-1,1\}^{\infty }$
is a compact abelian group with the pointwise product and the product topology. The Haar measure on
![]() $\{ -1,1\}^{\infty }$
is then just the countable product of the measure
$\{ -1,1\}^{\infty }$
is then just the countable product of the measure
![]() $\sigma _{1}$
. Clearly, the dual group of
$\sigma _{1}$
. Clearly, the dual group of
![]() $\{-1,1\}^{\mathbb {N}}$
is the set
$\{-1,1\}^{\mathbb {N}}$
is the set
![]() $\{\chi _{S}\colon S \in \mathcal {P}_{fin}(\mathbb {N})\}$
, where
$\{\chi _{S}\colon S \in \mathcal {P}_{fin}(\mathbb {N})\}$
, where
![]() $S\in \mathcal {P}_{fin}(\mathbb {N})$
means that
$S\in \mathcal {P}_{fin}(\mathbb {N})$
means that
![]() $|S|:=\mathrm {{card}}(S)<\infty $
and
$|S|:=\mathrm {{card}}(S)<\infty $
and
![]() $\chi _{S}\colon \{ -1,1\}^{\infty } \rightarrow \{-1,1\}$
is defined by
$\chi _{S}\colon \{ -1,1\}^{\infty } \rightarrow \{-1,1\}$
is defined by
![]() $\chi _{S}(x) = \prod _{n \in S}{x_{n}}$
for all
$\chi _{S}(x) = \prod _{n \in S}{x_{n}}$
for all
![]() $x = (x_{n})_{n \in \mathbb {N}}$
in
$x = (x_{n})_{n \in \mathbb {N}}$
in
![]() $\{ -1,1\}^{\infty }$
.
$\{ -1,1\}^{\infty }$
.
The compact abelian group
![]() $\mathbb {T}^{\infty }$
carries the pointwise product, the product topology and the product of the normalised Lebesgue measure on
$\mathbb {T}^{\infty }$
carries the pointwise product, the product topology and the product of the normalised Lebesgue measure on
![]() $\mathbb {T}^{\infty }$
as its Haar measure. Denote by
$\mathbb {T}^{\infty }$
as its Haar measure. Denote by
![]() $\mathbb {Z}^{(\mathbb {N})}$
the set of all sequences
$\mathbb {Z}^{(\mathbb {N})}$
the set of all sequences
![]() $\alpha =(\alpha _1, \ldots , \alpha _n, \ldots )$
of integers which vanish for n large enough. Then we have
$\alpha =(\alpha _1, \ldots , \alpha _n, \ldots )$
of integers which vanish for n large enough. Then we have
![]() $\widehat {\mathbb {T}^\infty }=\mathbb {Z}^{(\mathbb {N})}$
, where each
$\widehat {\mathbb {T}^\infty }=\mathbb {Z}^{(\mathbb {N})}$
, where each
![]() $\alpha \in \mathbb {Z}^{(\mathbb {N})}$
is identified with the character
$\alpha \in \mathbb {Z}^{(\mathbb {N})}$
is identified with the character
![]() $\gamma (z) = z^{\alpha }:=\prod _{j=1}^{\infty } z^{\alpha _j}$
,
$\gamma (z) = z^{\alpha }:=\prod _{j=1}^{\infty } z^{\alpha _j}$
,
![]() $z \in \mathbb {T}^\infty $
.
$z \in \mathbb {T}^\infty $
.
The subset of all sequences
![]() $\alpha \in \mathbb {Z}^{(\mathbb {N})}$
, for which all entries are either 0 or natural, is denoted by
$\alpha \in \mathbb {Z}^{(\mathbb {N})}$
, for which all entries are either 0 or natural, is denoted by
![]() $\mathbb {N}_0^{(\mathbb {N})}$
. We write
$\mathbb {N}_0^{(\mathbb {N})}$
. We write
![]() $\Lambda ^\leq (m,n) \subset \mathbb {N}_0^{(\mathbb {N})}$
for the subset of all
$\Lambda ^\leq (m,n) \subset \mathbb {N}_0^{(\mathbb {N})}$
for the subset of all
![]() $\alpha $
’s of length n and with order
$\alpha $
’s of length n and with order
![]() $|\alpha | = \sum _{j=1}^{n}\alpha _j \leq m$
, whereas
$|\alpha | = \sum _{j=1}^{n}\alpha _j \leq m$
, whereas
![]() $\Lambda ^=(m,n)$
consists of all
$\Lambda ^=(m,n)$
consists of all
![]() $\alpha $
’s of length n but with order
$\alpha $
’s of length n but with order
![]() $|\alpha | = m$
.
$|\alpha | = m$
.
Trigonometric polynomials. Given
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $m \in \mathbb {N}_0$
, we denote
$m \in \mathbb {N}_0$
, we denote
![]() $T(m,n)$
the set of all multi indices
$T(m,n)$
the set of all multi indices
![]() $\{\alpha \in \mathbb {Z}^n\colon |\alpha | \leq m\}$
and
$\{\alpha \in \mathbb {Z}^n\colon |\alpha | \leq m\}$
and
![]() $\mathcal {T}_{\leq m}(\mathbb {T}^n)$
the space of all trigonometric polynomials:
$\mathcal {T}_{\leq m}(\mathbb {T}^n)$
the space of all trigonometric polynomials:
 $$\begin{align*}P(z) = \sum_{\alpha \in T(m,n)} c_\alpha z^{\alpha}, \quad\, z\in \mathbb{T}^n \end{align*}$$
$$\begin{align*}P(z) = \sum_{\alpha \in T(m,n)} c_\alpha z^{\alpha}, \quad\, z\in \mathbb{T}^n \end{align*}$$
on the n-dimensional torus
![]() $\mathbb {T}^n$
which have degree
$\mathbb {T}^n$
which have degree
![]() $\text {deg}(P) = \max \{|\alpha |; \, c_\alpha \neq 0\} \leq m$
. Clearly,
$\text {deg}(P) = \max \{|\alpha |; \, c_\alpha \neq 0\} \leq m$
. Clearly,
![]() $\mathcal {T}_{\leq m}(\mathbb {T}^n)$
together with the sup norm
$\mathcal {T}_{\leq m}(\mathbb {T}^n)$
together with the sup norm
![]() $\|\cdot \|_{\mathbb {T}^n}$
(also denoted by
$\|\cdot \|_{\mathbb {T}^n}$
(also denoted by
![]() $\|\cdot \|_{\infty }$
) form a Banach space.
$\|\cdot \|_{\infty }$
) form a Banach space.
By
![]() $\mathcal {P}_{\leq m}(\mathbb {T}^n)$
, we denote the closed subspace of
$\mathcal {P}_{\leq m}(\mathbb {T}^n)$
, we denote the closed subspace of
![]() $\mathcal {T}_{\leq m}(\mathbb {T}^n)$
of all trigonometric analytic polynomials
$\mathcal {T}_{\leq m}(\mathbb {T}^n)$
of all trigonometric analytic polynomials
![]() $P(z)= \sum _{\alpha \in \Lambda ^{\leq }(m,n)} c_\alpha z^\alpha $
for all
$P(z)= \sum _{\alpha \in \Lambda ^{\leq }(m,n)} c_\alpha z^\alpha $
for all
![]() $z\in \mathbb {T}^n$
. The space
$z\in \mathbb {T}^n$
. The space
![]() $\mathcal {P}_{= m}(\mathbb {T}^n)$
is defined to be the closed subspace of all m-homogeneous polynomials P given by
$\mathcal {P}_{= m}(\mathbb {T}^n)$
is defined to be the closed subspace of all m-homogeneous polynomials P given by
![]() $P(z)= \sum _{\alpha \in \Lambda ^{=}(m,n)} c_\alpha z^\alpha $
.
$P(z)= \sum _{\alpha \in \Lambda ^{=}(m,n)} c_\alpha z^\alpha $
.
Moreover, we are going to make use of the so-called ‘hypercontractive’ Bohnenblust–Hille inequality: There is some universal constant
![]() $C>0$
, such that, for each
$C>0$
, such that, for each
![]() $m,n$
and
$m,n$
and
![]() $P \in \mathcal {P}_{\leq m}(\mathbb {T}^n)$
:
$P \in \mathcal {P}_{\leq m}(\mathbb {T}^n)$
:
 $$ \begin{align} \Big(\sum_{\alpha \in \Lambda^{\leq}(m,n)} |\widehat{P}(\alpha)|^{\frac{2m}{m+1}}\Big)^{\frac{m+1}{2m}} \leq C^{\sqrt{m \log m}} \|P\|_\infty\,; \end{align} $$
$$ \begin{align} \Big(\sum_{\alpha \in \Lambda^{\leq}(m,n)} |\widehat{P}(\alpha)|^{\frac{2m}{m+1}}\Big)^{\frac{m+1}{2m}} \leq C^{\sqrt{m \log m}} \|P\|_\infty\,; \end{align} $$
we refer to [Reference Bohnenblust and Hille5] (original form), [Reference Defant, Frerick, Ortega-Cerdá, Ounäıes and Seip8] (hypercontractive form), [Reference Bayart, Pellegrino and Seoane-Sepulveda2] (subexponential form) and within the context of Dirichlet series and holomorphic functions in infinitely many variables to the monograph [Reference Defant, García, Maestre and Sevilla Peris9].
A well-known consequence of Bernstein’s inequality (see, e.g. [Reference Queffélec and Queffélec20, Corollary 5.2.3]) is that, for all positive integers
![]() $n, m$
, there is a subset
$n, m$
, there is a subset
![]() $F \subset \mathbb {T}^n$
of cardinality card
$F \subset \mathbb {T}^n$
of cardinality card
![]() $F \leq (1+ 20 m)^n$
, such that, for every
$F \leq (1+ 20 m)^n$
, such that, for every
![]() $P \in \mathcal {T}_{\leq m}(\mathbb {T}^n)$
, we have:
$P \in \mathcal {T}_{\leq m}(\mathbb {T}^n)$
, we have:
In other terms, for
![]() $N = (1 + 20 m)^n$
, the linear mapping:
$N = (1 + 20 m)^n$
, the linear mapping:
is a
![]() $2$
-embedding of
$2$
-embedding of
![]() $\mathcal {T}_{\leq m}(\mathbb {T}^n)$
into
$\mathcal {T}_{\leq m}(\mathbb {T}^n)$
into
![]() $\ell ^N_\infty $
.
$\ell ^N_\infty $
.
3 A probabilistic proof
We use the famous Kahane–Salem–Zygmund inequality (the KSZ-inequality, see, e.g. [Reference Defant, García, Maestre and Sevilla Peris9, Reference Defant and Mastyło10], [Reference Kahane14] or [Reference Queffélec and Queffélec20]) to improve Theorem 1.1. Our argument is different from the original proof of Theorem 1.1, which we are going to analyse in the next section.
Theorem 3.1. Let
![]() $(\Omega , \mathcal {A}, \mathbb {P})$
be a probability measure space. Then there is a positive constant C, such that, for each
$(\Omega , \mathcal {A}, \mathbb {P})$
be a probability measure space. Then there is a positive constant C, such that, for each
![]() $m,n \in \mathbb {N}$
and for every trigonometric random polynomial
$m,n \in \mathbb {N}$
and for every trigonometric random polynomial
![]() $P(\omega , z)= \sum _{\alpha \in T(m,n)} \varepsilon _\alpha (\omega ) c_\alpha z^\alpha $
,
$P(\omega , z)= \sum _{\alpha \in T(m,n)} \varepsilon _\alpha (\omega ) c_\alpha z^\alpha $
,
![]() $(\omega , z) \in \Omega \times \mathbb {T}^n$
, one has:
$(\omega , z) \in \Omega \times \mathbb {T}^n$
, one has:
where
![]() $(\varepsilon _\alpha )_{\alpha \in T(m,n)}$
is a sequence of Bernoulli variables on
$(\varepsilon _\alpha )_{\alpha \in T(m,n)}$
is a sequence of Bernoulli variables on
![]() $(\Omega , \mathcal {A}, \mathbb {P})$
.
$(\Omega , \mathcal {A}, \mathbb {P})$
.
As we will see in Theorem 3.3, the following consequence of the KSZ-inequality gives Kislyakov’s multiplier Theorem 1.1 as a particular case.
Theorem 3.2. There is a positive constant C, such that for all
![]() $n,m \in \mathbb {N}$
, all Banach spaces
$n,m \in \mathbb {N}$
, all Banach spaces
![]() $F=(\mathbb {C}^{T(m,n)},\|\cdot \|)$
and for all sequences
$F=(\mathbb {C}^{T(m,n)},\|\cdot \|)$
and for all sequences
![]() $\xi =(\xi _\alpha )_{\alpha \in T(m,n)}$
:
$\xi =(\xi _\alpha )_{\alpha \in T(m,n)}$
:
Proof. Let
![]() $(\varepsilon _\alpha )_{\alpha \in T(m,n)}$
be a sequence of Bernoulli variables on some probability space
$(\varepsilon _\alpha )_{\alpha \in T(m,n)}$
be a sequence of Bernoulli variables on some probability space
![]() $(\Omega , \mathcal {A}, \mathbb {P})$
, and consider the following three operators:
$(\Omega , \mathcal {A}, \mathbb {P})$
, and consider the following three operators:
 $$ \begin{align*} & R_\xi\colon \ell_2(T(m,n)) \to F,\,\, (c_\alpha) \mapsto (c_\alpha \xi_\alpha), \\[2ex]& \phi_{K\!SZ}\colon \ell_2(T(m,n)) \to L_1(\mathbb{P}, \mathcal{T}_{\leq m}(\mathbb{T}^n)) ,\,\, (c_\alpha) \mapsto \sum_{\alpha \in T(m,n) } \varepsilon_\alpha(\cdot) c_\alpha z^\alpha, \\& L_\xi\colon L_1(\mathbb{P}, \mathcal{T}_{\leq m}(\mathbb{T}^n)) \to F,\,\,\, \sum_{\alpha \in T(m,n)} \varepsilon_\alpha(\cdot) c_\alpha z^\alpha \mapsto (c_\alpha \xi_\alpha). \end{align*} $$
$$ \begin{align*} & R_\xi\colon \ell_2(T(m,n)) \to F,\,\, (c_\alpha) \mapsto (c_\alpha \xi_\alpha), \\[2ex]& \phi_{K\!SZ}\colon \ell_2(T(m,n)) \to L_1(\mathbb{P}, \mathcal{T}_{\leq m}(\mathbb{T}^n)) ,\,\, (c_\alpha) \mapsto \sum_{\alpha \in T(m,n) } \varepsilon_\alpha(\cdot) c_\alpha z^\alpha, \\& L_\xi\colon L_1(\mathbb{P}, \mathcal{T}_{\leq m}(\mathbb{T}^n)) \to F,\,\,\, \sum_{\alpha \in T(m,n)} \varepsilon_\alpha(\cdot) c_\alpha z^\alpha \mapsto (c_\alpha \xi_\alpha). \end{align*} $$
Clearly,
![]() $R_\xi = L_\xi \circ \phi _{K\!SZ}$
and:
$R_\xi = L_\xi \circ \phi _{K\!SZ}$
and:
Moreover, by the KSZ-inequality from Theorem 3.1, we get:
We claim that:
Indeed, given a random polynomial
![]() $P\in L_1(\mathbb {P}, \mathcal {T}_{\leq m}(\mathbb {T}^n))$
given by:
$P\in L_1(\mathbb {P}, \mathcal {T}_{\leq m}(\mathbb {T}^n))$
given by:
 $$\begin{align*}P(\omega,z)=\sum_{\alpha \in T(m,n)} \varepsilon_\alpha(\omega) c_\alpha z^{\alpha}, \quad\, (\omega, z) \in \Omega \times \mathbb{T}^n. \end{align*}$$
$$\begin{align*}P(\omega,z)=\sum_{\alpha \in T(m,n)} \varepsilon_\alpha(\omega) c_\alpha z^{\alpha}, \quad\, (\omega, z) \in \Omega \times \mathbb{T}^n. \end{align*}$$
Then, for every
![]() $\omega \in \Omega $
, we have:
$\omega \in \Omega $
, we have:
Now integrating proves the claim. All together yields:
 $$ \begin{align*} \sup_{\|\mu\|_{\ell_2(T(m,n))}\leq 1} & \|(\mu_{\alpha} \xi_\alpha)_{\alpha \in T(m,n)}\|_F \\ & \leq \|L_\xi\|\, \|\phi_{KSZ}\| \leq C \sqrt{n \log (1+m)}\,\big\|M_\xi\colon \mathcal{T}_{\leq m}(\mathbb{T}^n)\to F\big\|, \end{align*} $$
$$ \begin{align*} \sup_{\|\mu\|_{\ell_2(T(m,n))}\leq 1} & \|(\mu_{\alpha} \xi_\alpha)_{\alpha \in T(m,n)}\|_F \\ & \leq \|L_\xi\|\, \|\phi_{KSZ}\| \leq C \sqrt{n \log (1+m)}\,\big\|M_\xi\colon \mathcal{T}_{\leq m}(\mathbb{T}^n)\to F\big\|, \end{align*} $$
and so this completes the proof.
Now by Theorem 3.2, we deduce that Kislyakov’s original Theorem 1.1 is a special case of the following more general result.
Corollary 3.3. Let V be a closed subspace of
![]() $L_\infty (\mathbb {T}^\infty )$
. Then for every
$L_\infty (\mathbb {T}^\infty )$
. Then for every
![]() $\ell _1(\mathbb {Z}^{(\mathbb {N})})$
-multiplier
$\ell _1(\mathbb {Z}^{(\mathbb {N})})$
-multiplier
![]() $\xi = (\xi _\alpha )_{\alpha \in \mathbb {Z}^{(\mathbb {N})}}$
of V, one has:
$\xi = (\xi _\alpha )_{\alpha \in \mathbb {Z}^{(\mathbb {N})}}$
of V, one has:
 $$ \begin{align*} \sup_{n,m \in \mathbb{ N}}\,\,\,\,\frac{1}{\sqrt{n \log (1+m)}} \bigg(\sum_{\alpha \in \Gamma \cap T(m,n)} & |\xi_{\alpha}|^2\bigg)^{1/2} \,\,\,< \infty, \end{align*} $$
$$ \begin{align*} \sup_{n,m \in \mathbb{ N}}\,\,\,\,\frac{1}{\sqrt{n \log (1+m)}} \bigg(\sum_{\alpha \in \Gamma \cap T(m,n)} & |\xi_{\alpha}|^2\bigg)^{1/2} \,\,\,< \infty, \end{align*} $$
where:
 $$\begin{align*}\Gamma = \bigcup_{f \in V} \operatorname{\mathrm{supp}} \widehat{f}\subset \mathbb{Z}^{(\mathbb{N})} . \end{align*}$$
$$\begin{align*}\Gamma = \bigcup_{f \in V} \operatorname{\mathrm{supp}} \widehat{f}\subset \mathbb{Z}^{(\mathbb{N})} . \end{align*}$$
In particular, every
![]() $\ell _1(\mathbb {N}_0^{(\mathbb {N})})$
-multiplier of
$\ell _1(\mathbb {N}_0^{(\mathbb {N})})$
-multiplier of
![]() $H^\infty (\mathbb {T}^\infty )$
satisfies the preceding estimate whenever we replace
$H^\infty (\mathbb {T}^\infty )$
satisfies the preceding estimate whenever we replace
![]() $\Gamma \cap T(m,n)$
by
$\Gamma \cap T(m,n)$
by
![]() $\Lambda ^{\leq }(m,n)$
and every
$\Lambda ^{\leq }(m,n)$
and every
![]() $\ell _1(\mathbb {N}_0^{(\mathbb {N})})$
-multiplier of
$\ell _1(\mathbb {N}_0^{(\mathbb {N})})$
-multiplier of
![]() $C^A(\mathbb {T}^\infty )$
satisfies the estimate from (1.1).
$C^A(\mathbb {T}^\infty )$
satisfies the estimate from (1.1).
Proof. Let us prove the first statement. For a fixed
![]() $\xi = (\xi _{\alpha })_{\alpha \in \mathbb {Z}^{(\mathbb {N})}}$
, we can define a new sequence
$\xi = (\xi _{\alpha })_{\alpha \in \mathbb {Z}^{(\mathbb {N})}}$
, we can define a new sequence
![]() $\xi ' = (\xi _{\alpha }')_{\alpha \in \mathbb {Z}^{(\mathbb {N})}}$
with
$\xi ' = (\xi _{\alpha }')_{\alpha \in \mathbb {Z}^{(\mathbb {N})}}$
with
![]() $\xi ^{\prime }_{\alpha } = \xi _{\alpha }$
if
$\xi ^{\prime }_{\alpha } = \xi _{\alpha }$
if
![]() $\alpha \in \Gamma $
and
$\alpha \in \Gamma $
and
![]() $\xi ^{\prime }_{\alpha } = 0$
otherwise. It is clear that
$\xi ^{\prime }_{\alpha } = 0$
otherwise. It is clear that
![]() $\xi $
is a
$\xi $
is a
![]() $\ell _{1}(\mathbb {Z}^{(\mathbb {N})})$
-multiplier if and only if so does
$\ell _{1}(\mathbb {Z}^{(\mathbb {N})})$
-multiplier if and only if so does
![]() $\xi '$
. Thus, applying Theorem 3.2 to
$\xi '$
. Thus, applying Theorem 3.2 to
![]() $\xi '$
, we immediately conclude the result. For the second statement, note that:
$\xi '$
, we immediately conclude the result. For the second statement, note that:
 $$ \begin{align*} \Big(\sum_{\alpha \in \mathbb{N}_0^n \colon \max\{\alpha_1,\ldots,\alpha_n\}\leq m}& |\xi_{\alpha}|^2\Big)^{\frac{1}{2}} \leq \Big(\sum_{|\alpha| \leq mn} |\xi_{\alpha}|^2\Big)^{\frac{1}{2}} \\ & \leq C \,\sqrt{n \log (1+mn)}\,\,\big\|M_\xi\colon \mathcal{P}_{\leq mn}(\mathbb{T}^n) \to \ell_1(\Lambda^{\leq }(mn,n))\big\| \\ & \leq C \,\sqrt{n \log (1+mn)}\,\,\big\|M_\xi \colon C^A(\mathbb{T}^n) \to \ell_1(\mathbb{N}_0^n)\big\|, \end{align*} $$
$$ \begin{align*} \Big(\sum_{\alpha \in \mathbb{N}_0^n \colon \max\{\alpha_1,\ldots,\alpha_n\}\leq m}& |\xi_{\alpha}|^2\Big)^{\frac{1}{2}} \leq \Big(\sum_{|\alpha| \leq mn} |\xi_{\alpha}|^2\Big)^{\frac{1}{2}} \\ & \leq C \,\sqrt{n \log (1+mn)}\,\,\big\|M_\xi\colon \mathcal{P}_{\leq mn}(\mathbb{T}^n) \to \ell_1(\Lambda^{\leq }(mn,n))\big\| \\ & \leq C \,\sqrt{n \log (1+mn)}\,\,\big\|M_\xi \colon C^A(\mathbb{T}^n) \to \ell_1(\mathbb{N}_0^n)\big\|, \end{align*} $$
which completes the argument.
Note that Corollary 4.5 below recovers the preceding result — using a different technique of proof with the advantage of slightly more explicit constants.
4 Variants for compact abelian groups
Based on local Banach space theory and inspired by ideas from [Reference Kislyakov15], we improve Theorem 3.2 and its Corollary 3.3. Our more abstract approach has the advantage that it allows to consider more general compact abelian groups instead of only the multidimensional torus. The main result here is Theorem 4.4 below.
We start with the following basic lemma which is a simple consequence of Lemma 2.1 and crucial for our purpose.
Lemma 4.1. Let G be a compact abelian group,
![]() $\Gamma $
a finite subset in
$\Gamma $
a finite subset in
![]() $\widehat {G}$
and
$\widehat {G}$
and
![]() $F:=(\mathbb {C}^{\Gamma }, \|\cdot \|)$
a Banach space. Then for every
$F:=(\mathbb {C}^{\Gamma }, \|\cdot \|)$
a Banach space. Then for every
![]() $\xi = (\xi _\gamma )_{\gamma \in \Gamma }$
:
$\xi = (\xi _\gamma )_{\gamma \in \Gamma }$
:
Proof. The second equality is obvious, and from Lemma 2.1 and the orthogonality of the characters in
![]() $L_2(\nu )$
(where
$L_2(\nu )$
(where
![]() $\nu $
denotes the normalised Haar measure on G), we easily deduce that:
$\nu $
denotes the normalised Haar measure on G), we easily deduce that:
To see the reverse estimate, note that for every
![]() $f \in C_\Gamma $
, one has:
$f \in C_\Gamma $
, one has:
 $$ \begin{align*} \|M_\xi f\|_F = \|(\xi_\gamma \widehat{f}(\gamma))\|_F & \leq \|D_\xi\colon \ell_2(\Gamma) \to F\|\,\|(\widehat{f}(\gamma))\|_{\ell_2(\Gamma)} \\ & = \|D_\xi\colon \ell_2(\Gamma) \to F\|\, \Big(\int_{G} |f(x)|^2d\nu(x)\Big)^{\frac{1}{2}}, \end{align*} $$
$$ \begin{align*} \|M_\xi f\|_F = \|(\xi_\gamma \widehat{f}(\gamma))\|_F & \leq \|D_\xi\colon \ell_2(\Gamma) \to F\|\,\|(\widehat{f}(\gamma))\|_{\ell_2(\Gamma)} \\ & = \|D_\xi\colon \ell_2(\Gamma) \to F\|\, \Big(\int_{G} |f(x)|^2d\nu(x)\Big)^{\frac{1}{2}}, \end{align*} $$
where we have used the Plancherel theorem for groups. Then, Pietsch domination theorem yields that:
As a very first application of the preceding lemma, we obtain an interesting reformulation of Theorem 3.2.
Corollary 4.2. There is
![]() $C>0$
, such that for all
$C>0$
, such that for all
![]() $n,m \in \mathbb {N}$
, all Banach spaces
$n,m \in \mathbb {N}$
, all Banach spaces
![]() $F=(\mathbb {C}^{T(m,n)},\|\cdot \|)$
and all
$F=(\mathbb {C}^{T(m,n)},\|\cdot \|)$
and all
![]() $\xi =(\xi _\alpha )_{\alpha \in T(m,n)}$
:
$\xi =(\xi _\alpha )_{\alpha \in T(m,n)}$
:
In view of Bernstein’s theorem from (2.2), the next result is a strong extension despite the cotype assumption. It will allow us to get the Kislyakov type multiplier theorems (in particular, Theorem 4.4) for compact abelian groups different from the multidimensional torus.
Proposition 4.3. Let
![]() $I\colon X \hookrightarrow \ell _\infty ^N$
be a
$I\colon X \hookrightarrow \ell _\infty ^N$
be a
![]() $\lambda $
-embedding and F a Banach space. Then for every operator
$\lambda $
-embedding and F a Banach space. Then for every operator
![]() $T\colon X \to F$
:
$T\colon X \to F$
:
Proof. Define for each
![]() $N \in \mathbb {N}$
the N-th harmonic number
$N \in \mathbb {N}$
the N-th harmonic number
![]() $ h_N := \sum _{j=1}^N \frac {1}{j}\, $
and the discrete measure
$ h_N := \sum _{j=1}^N \frac {1}{j}\, $
and the discrete measure
![]() $\mu _N$
on the power set of
$\mu _N$
on the power set of
![]() $\{1, \ldots , N\}$
given by
$\{1, \ldots , N\}$
given by
![]() $\mu _N(\{j\}) := \frac {1}{j}$
. for each
$\mu _N(\{j\}) := \frac {1}{j}$
. for each
![]() $j\in \{1,\ldots , N\}$
. In what follows, we need the elementary observations that
$j\in \{1,\ldots , N\}$
. In what follows, we need the elementary observations that
![]() $ \log N < h_N \leq 1+\log N $
and for every
$ \log N < h_N \leq 1+\log N $
and for every
![]() $\xi = (\xi _i)_{i=1}^{N}\in \mathbb {C}^N$
:
$\xi = (\xi _i)_{i=1}^{N}\in \mathbb {C}^N$
:
Indeed, if
![]() $\| \xi \|_{\ell _{\infty }^{N}} = |\xi _{k}|$
for some
$\| \xi \|_{\ell _{\infty }^{N}} = |\xi _{k}|$
for some
![]() $k\in \{1, \ldots , N\}$
, then:
$k\in \{1, \ldots , N\}$
, then:
 $$\begin{align*}\Big(\sum_{j=1}^{N} \frac{1}{j}|\xi_{j}|^{h_{N}} \Big)^{\frac{1}{h_{N}}} \, \geq \, \frac{1}{k^{1/h_{N}}}\,|\xi_{k}| = e^{-\frac{\log{k}}{h_{N}}} \, |\xi_{k}| \geq e^{-\frac{\log{k}}{\log{N}}} \, |\xi_{k}| \geq e^{-1} \, |\xi_{k}|. \end{align*}$$
$$\begin{align*}\Big(\sum_{j=1}^{N} \frac{1}{j}|\xi_{j}|^{h_{N}} \Big)^{\frac{1}{h_{N}}} \, \geq \, \frac{1}{k^{1/h_{N}}}\,|\xi_{k}| = e^{-\frac{\log{k}}{h_{N}}} \, |\xi_{k}| \geq e^{-\frac{\log{k}}{\log{N}}} \, |\xi_{k}| \geq e^{-1} \, |\xi_{k}|. \end{align*}$$
It is well known that, for every operator
![]() $S\colon E\to F$
between Banach spaces and
$S\colon E\to F$
between Banach spaces and
![]() $2 \leq p < \infty $
, one has:
$2 \leq p < \infty $
, one has:
where
![]() $K_p \leq \sqrt {p}$
is the best constant from the right-hand side of Khinchine’s inequality for Rademacher p-averages (see [Reference Pisier19, Theorem 5.15]).
$K_p \leq \sqrt {p}$
is the best constant from the right-hand side of Khinchine’s inequality for Rademacher p-averages (see [Reference Pisier19, Theorem 5.15]).
Consider the following obvious factorisation of an operator
![]() $T \colon X \to F$
:
$T \colon X \to F$
:
Thus, the above facts combined with the ideal properties of p-summing operators yield:
 $$ \begin{align*} \pi_2(T) & \leq \|I\|\,\pi_2(T \circ I^{-1}) \leq \|I\|\,\sqrt{h_N} \,C_2(F)\,\pi_{h_N} (T \circ I^{-1})\\ & \leq \|I\|\,\|I^{-1}\|\,\|T\|\,\sqrt{h_N}\,C_2(F)\,\pi_{h_N} (\text{id}_{I(X)})\\ & \leq \|T\|\, C_2(F)\,\sqrt{h_N} \,\lambda \,\pi_{h_N} (\text{id}_{\ell_\infty^N}). \end{align*} $$
$$ \begin{align*} \pi_2(T) & \leq \|I\|\,\pi_2(T \circ I^{-1}) \leq \|I\|\,\sqrt{h_N} \,C_2(F)\,\pi_{h_N} (T \circ I^{-1})\\ & \leq \|I\|\,\|I^{-1}\|\,\|T\|\,\sqrt{h_N}\,C_2(F)\,\pi_{h_N} (\text{id}_{I(X)})\\ & \leq \|T\|\, C_2(F)\,\sqrt{h_N} \,\lambda \,\pi_{h_N} (\text{id}_{\ell_\infty^N}). \end{align*} $$
Since
![]() $\|\text {id}\colon L_{h_N}(\mu _N) \to \ell _\infty ^N \| \leq e$
, it follows that:
$\|\text {id}\colon L_{h_N}(\mu _N) \to \ell _\infty ^N \| \leq e$
, it follows that:
The following theorem is the main result of this section, and we want to mention once again that its proof is very much inspired by [Reference Kislyakov15, Theorem 6].
Theorem 4.4. Let G be a compact abelian group and
![]() $\Gamma $
a finite subset in
$\Gamma $
a finite subset in
![]() $\widehat {G}$
. Assume that
$\widehat {G}$
. Assume that
![]() $I\colon C_{\Gamma } \to \ell _\infty ^N$
is a
$I\colon C_{\Gamma } \to \ell _\infty ^N$
is a
![]() $\lambda $
-embedding and
$\lambda $
-embedding and
![]() $F:=(\mathbb {C}^{\Gamma }, \|\cdot \|)$
a Banach space. Then, for every
$F:=(\mathbb {C}^{\Gamma }, \|\cdot \|)$
a Banach space. Then, for every
![]() $\xi =(\xi _\gamma )_{\gamma \in \Gamma } \in \mathbb {C}^\Gamma $
, one has:
$\xi =(\xi _\gamma )_{\gamma \in \Gamma } \in \mathbb {C}^\Gamma $
, one has:
Comparing with Theorem 3.2, we see that the price we pay for the fact that the theorem applies to more general groups than the multidimensional tori is that the estimate involves the cotype constant of F.
Proof. By Lemma 4.3 and Bernstein’s embedding from (2.2), we get:
Thus, it follows from Lemma 2.1 that for all
![]() $f \in C_\Gamma $
:
$f \in C_\Gamma $
:
 $$ \begin{align*} \|(\widehat{f}(\gamma)\xi_{\gamma})\|_F & \leq e^2\, \lambda \, C_{2}(F) \, \sqrt{1+\log N} \, \|M_\xi \colon C_\Gamma \to F\| \Big(\int_G |f(g)|^2\,d\nu \Big)^{\frac{1}{2}} \\ & = e^2\, \lambda \, C_{2}(F) \, \sqrt{1+\log N} \,\|M_\xi \colon C_\Gamma \to F\| \Big(\sum_{\gamma \in \Gamma} |\widehat{f}(\gamma)|^2\Big)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} \|(\widehat{f}(\gamma)\xi_{\gamma})\|_F & \leq e^2\, \lambda \, C_{2}(F) \, \sqrt{1+\log N} \, \|M_\xi \colon C_\Gamma \to F\| \Big(\int_G |f(g)|^2\,d\nu \Big)^{\frac{1}{2}} \\ & = e^2\, \lambda \, C_{2}(F) \, \sqrt{1+\log N} \,\|M_\xi \colon C_\Gamma \to F\| \Big(\sum_{\gamma \in \Gamma} |\widehat{f}(\gamma)|^2\Big)^{\frac{1}{2}}. \end{align*} $$
Then the conclusion follows by duality.
We finish with the following improvement of Corollary 3.3; its proof is an immediate consequence of Theorem 4.4, Bernstein’s embedding from (2.2), the fact that
![]() $C_2(\ell _p(\mathbb {Z}^{n})) \leq \sqrt {2}$
for
$C_2(\ell _p(\mathbb {Z}^{n})) \leq \sqrt {2}$
for
![]() $1 \leq p \leq 2$
and, that by Hölder’s inequality, we have:
$1 \leq p \leq 2$
and, that by Hölder’s inequality, we have:
 $$\begin{align*}\Big(\sum_{\gamma \in \Gamma} |\xi_{\gamma}|^r\Big)^{1/r} = \sup_{\|\mu \|_{\ell_2(\Gamma)}\leq 1} \|(\mu_\gamma \xi_\gamma )\|_{\ell_p(\Gamma)}, \quad\, (\xi_\gamma) \in \ell_r(\Gamma) \end{align*}$$
$$\begin{align*}\Big(\sum_{\gamma \in \Gamma} |\xi_{\gamma}|^r\Big)^{1/r} = \sup_{\|\mu \|_{\ell_2(\Gamma)}\leq 1} \|(\mu_\gamma \xi_\gamma )\|_{\ell_p(\Gamma)}, \quad\, (\xi_\gamma) \in \ell_r(\Gamma) \end{align*}$$
for all
![]() $1 \leq p \leq 2$
with
$1 \leq p \leq 2$
with
![]() $\frac {1}{r} = \frac {1}{p}-\frac {1}{2}$
.
$\frac {1}{r} = \frac {1}{p}-\frac {1}{2}$
.
Corollary 4.5. Let
![]() $1 \leq p \leq 2$
and
$1 \leq p \leq 2$
and
![]() $\frac {1}{r} = \frac {1}{p}-\frac {1}{2}$
. Then, for each
$\frac {1}{r} = \frac {1}{p}-\frac {1}{2}$
. Then, for each
![]() $n,m \in \mathbb {N}$
, and for every
$n,m \in \mathbb {N}$
, and for every
![]() $\xi =(\xi _\alpha )_{\alpha \in \mathbb {Z}^n, |\alpha | \leq m}$
, the following estimate holds:
$\xi =(\xi _\alpha )_{\alpha \in \mathbb {Z}^n, |\alpha | \leq m}$
, the following estimate holds:
 $$ \begin{align*} \Big(\sum_{\alpha \in \mathbb{Z}^n, |\alpha| \leq m} & |\xi_{\alpha}|^r\Big)^{1/r} \\& \leq 2\sqrt{2}e^2 \,\sqrt{n \log (1+20m)}\,\,\big\|M_\xi\colon \mathcal{T}_{\leq m}(\mathbb{T}^n)\to \ell_p\big(\{\alpha \in \mathbb{Z}^n\colon |\alpha| \leq m\}\big)\big\|. \end{align*} $$
$$ \begin{align*} \Big(\sum_{\alpha \in \mathbb{Z}^n, |\alpha| \leq m} & |\xi_{\alpha}|^r\Big)^{1/r} \\& \leq 2\sqrt{2}e^2 \,\sqrt{n \log (1+20m)}\,\,\big\|M_\xi\colon \mathcal{T}_{\leq m}(\mathbb{T}^n)\to \ell_p\big(\{\alpha \in \mathbb{Z}^n\colon |\alpha| \leq m\}\big)\big\|. \end{align*} $$
The following remarks suggest that this corollary leaves some space for improvements. Given
![]() $1 \leq p < \infty $
, consider again the multiplication operator:
$1 \leq p < \infty $
, consider again the multiplication operator:
If
![]() $2 \leq p < \infty $
, then:
$2 \leq p < \infty $
, then:
whereas for
![]() $\frac {2m}{m+1} \leq p \leq 2$
by the hypercontractive BH-inequality (2.1):
$\frac {2m}{m+1} \leq p \leq 2$
by the hypercontractive BH-inequality (2.1):
Hence, in view of Corollary 4.5, the complex interpolation between the extreme cases
![]() $\ell _1(\Gamma )$
and
$\ell _1(\Gamma )$
and
![]() $\ell _{\frac {2m}{m+1}}(\Gamma )$
suggests the following conjecture.
$\ell _{\frac {2m}{m+1}}(\Gamma )$
suggests the following conjecture.
Conjecture 4.6. Let
![]() $1 \leq p \leq \frac {2m}{m+1}$
and
$1 \leq p \leq \frac {2m}{m+1}$
and
![]() $\frac {1}{s} = \frac {m}{m-1}\big (\frac {1}{p}-\frac {m+1}{2m}\big )$
. Then, there exists a universal constant
$\frac {1}{s} = \frac {m}{m-1}\big (\frac {1}{p}-\frac {m+1}{2m}\big )$
. Then, there exists a universal constant
![]() $C>0$
, such that for each
$C>0$
, such that for each
![]() $n,m \in \mathbb {N}$
, and for every
$n,m \in \mathbb {N}$
, and for every
![]() $\xi =(\xi _\alpha )_{\alpha \in \Lambda ^{\leq }(m,n)}$
,
$\xi =(\xi _\alpha )_{\alpha \in \Lambda ^{\leq }(m,n)}$
,
 $$\begin{align*}\Big(\sum_{\alpha \in \Lambda^{\leq}(m,n)} |\xi_{\alpha}|^s\Big)^{1/s} \leq C^{\frac{m}{s}} \,(n \log (1+20m))^{\frac{1}{s}}\,\, \|M_\xi:\mathcal{P}_{\leq m}(\mathbb{T}^n) \to \ell_p(\Lambda^{\leq}(m,n))\|. \end{align*}$$
$$\begin{align*}\Big(\sum_{\alpha \in \Lambda^{\leq}(m,n)} |\xi_{\alpha}|^s\Big)^{1/s} \leq C^{\frac{m}{s}} \,(n \log (1+20m))^{\frac{1}{s}}\,\, \|M_\xi:\mathcal{P}_{\leq m}(\mathbb{T}^n) \to \ell_p(\Lambda^{\leq}(m,n))\|. \end{align*}$$
5 Variants by interpolation
The purpose of this section is to prove two variants of Kislyakov’s Theorem 3.3, both based on Theorem 4.4 and interpolation methods. We at first recall some notation from interpolation theory (see, e.g. [Reference Bergh and Löfström3]). The pair
![]() $\vec {X}=(X_0,X_1)$
of Banach spaces is called a Banach couple if there exists a Hausdorff topological vector space
$\vec {X}=(X_0,X_1)$
of Banach spaces is called a Banach couple if there exists a Hausdorff topological vector space
![]() $\mathcal {X}$
, such that
$\mathcal {X}$
, such that
![]() $X_j\hookrightarrow \mathcal {X}$
,
$X_j\hookrightarrow \mathcal {X}$
,
![]() $j=0, 1$
. A mapping
$j=0, 1$
. A mapping
![]() $\mathcal {F}$
, acting on the class of all Banach couples, is called an interpolation functor if for every couple
$\mathcal {F}$
, acting on the class of all Banach couples, is called an interpolation functor if for every couple
![]() $\vec {X} = (X_0, X_1)$
,
$\vec {X} = (X_0, X_1)$
,
![]() $\mathcal {F}(\vec {X})$
is a Banach space which is intermediate with respect to
$\mathcal {F}(\vec {X})$
is a Banach space which is intermediate with respect to
![]() $\vec {X}$
(i.e.
$\vec {X}$
(i.e.
![]() $X_0\cap X_1 \subset \mathcal {F}(\vec {X}) \subset X_0 + X_1$
) and
$X_0\cap X_1 \subset \mathcal {F}(\vec {X}) \subset X_0 + X_1$
) and
![]() $T\colon \mathcal {F}(\vec {X}) \to \mathcal {F}(\vec {Y})$
is bounded for every operator
$T\colon \mathcal {F}(\vec {X}) \to \mathcal {F}(\vec {Y})$
is bounded for every operator
![]() $T\colon \vec {X} \to \vec {Y}$
(meaning
$T\colon \vec {X} \to \vec {Y}$
(meaning
![]() $T\colon X_0 + X_1 \to Y_0 + Y_1$
is linear and its restrictions
$T\colon X_0 + X_1 \to Y_0 + Y_1$
is linear and its restrictions
![]() $T\colon X_j \to Y_j$
,
$T\colon X_j \to Y_j$
,
![]() $j=0,1$
are defined and bounded). If, additionally, there is a constant
$j=0,1$
are defined and bounded). If, additionally, there is a constant
![]() $C>0$
, such that for each
$C>0$
, such that for each
![]() $T\colon \vec {X} \to \vec {Y}$
:
$T\colon \vec {X} \to \vec {Y}$
:
where
![]() $\|T\colon \vec {X} \to \vec {Y}\|:= \max \{\|T\colon X_0 \to Y_0\|, \, \|T\colon X_1 \to Y_1\|\}$
, then
$\|T\colon \vec {X} \to \vec {Y}\|:= \max \{\|T\colon X_0 \to Y_0\|, \, \|T\colon X_1 \to Y_1\|\}$
, then
![]() $\mathcal {F}$
is called bounded. Clearly,
$\mathcal {F}$
is called bounded. Clearly,
![]() $C\geq 1$
, and if
$C\geq 1$
, and if
![]() $C=1$
, then
$C=1$
, then
![]() $\mathcal {F}$
is called exact.
$\mathcal {F}$
is called exact.
For an exact interpolation functor
![]() $\mathcal {F}$
, we define the fundamental function
$\mathcal {F}$
, we define the fundamental function
![]() $\psi _{\mathcal {F}}$
of
$\psi _{\mathcal {F}}$
of
![]() $\mathcal {F}$
by:
$\mathcal {F}$
by:
where the supremum is taken over all Banach couples
![]() $\vec {X}$
,
$\vec {X}$
,
![]() $\vec {Y}$
and all operators
$\vec {Y}$
and all operators
![]() $T\colon \vec {X} \to \vec {Y}$
, such that
$T\colon \vec {X} \to \vec {Y}$
, such that
![]() $\|T\colon X_0 \to Y_0\|\leq s$
and
$\|T\colon X_0 \to Y_0\|\leq s$
and
![]() $\|T\colon X_1 \to Y_1\| \leq t$
.
$\|T\colon X_1 \to Y_1\| \leq t$
.
Theorem 5.1. Let G be a compact abelian group and
![]() $\Gamma $
a finite subset in
$\Gamma $
a finite subset in
![]() $\widehat {G}$
. Suppose that
$\widehat {G}$
. Suppose that
![]() $\mathcal {F}$
is an exact interpolation functor with the fundamental function
$\mathcal {F}$
is an exact interpolation functor with the fundamental function
![]() $\psi _{\mathcal {F}}$
. Given two norms
$\psi _{\mathcal {F}}$
. Given two norms
![]() $\|\cdot \|_1$
and
$\|\cdot \|_1$
and
![]() $\|\cdot \|_2$
on
$\|\cdot \|_2$
on
![]() $\mathbb {C}^{\Gamma }$
define:
$\mathbb {C}^{\Gamma }$
define:
Then, for every
![]() $(\xi _\gamma )_{\gamma \in \Gamma } \in \mathbb {C}^{\Gamma }$
, one has:
$(\xi _\gamma )_{\gamma \in \Gamma } \in \mathbb {C}^{\Gamma }$
, one has:
 $$ \begin{align*} \sup_{\|\mu\|_{\ell_2(\Gamma)}\leq 1} &\|(\mu_{\gamma} \xi_\gamma)_{\gamma \in \Gamma}\|_F \\ & \leq \psi_{\mathcal{F}}(1, 1)\,\psi_{\mathcal{F}} \big(\pi_2(M_\xi \colon C_\Gamma \to (\mathbb{C}^{\Gamma},\|\cdot\|_1)),\, \pi_2(M_\xi \colon C_\Gamma \to (\mathbb{C}^{\Gamma},\|\cdot\|_2))\big). \end{align*} $$
$$ \begin{align*} \sup_{\|\mu\|_{\ell_2(\Gamma)}\leq 1} &\|(\mu_{\gamma} \xi_\gamma)_{\gamma \in \Gamma}\|_F \\ & \leq \psi_{\mathcal{F}}(1, 1)\,\psi_{\mathcal{F}} \big(\pi_2(M_\xi \colon C_\Gamma \to (\mathbb{C}^{\Gamma},\|\cdot\|_1)),\, \pi_2(M_\xi \colon C_\Gamma \to (\mathbb{C}^{\Gamma},\|\cdot\|_2))\big). \end{align*} $$
Note that Lemma 4.1 shows:
Hence, the proof of Theorem 5.1 is straightforward: It follows from the definition of the function
![]() $\psi _{\mathcal {F}}$
that, for any operator
$\psi _{\mathcal {F}}$
that, for any operator
![]() $T\colon \vec {X} \to \vec {Y}$
between the Banach couples
$T\colon \vec {X} \to \vec {Y}$
between the Banach couples
![]() $\vec {X} = (X_0, X_1)$
and
$\vec {X} = (X_0, X_1)$
and
![]() $\vec {Y}=(Y_0, Y_1)$
, we have:
$\vec {Y}=(Y_0, Y_1)$
, we have:
In particular, this implies that, for any Banach space Y,
5.1 Variant I
Theorem 5.2. Let G be a compact abelian group,
![]() $\Gamma $
a finite subset in
$\Gamma $
a finite subset in
![]() $\widehat {G}$
and
$\widehat {G}$
and
![]() $I\colon C_\Gamma \to \ell _\infty ^N$
a
$I\colon C_\Gamma \to \ell _\infty ^N$
a
![]() $\lambda $
-embedding. Suppose that
$\lambda $
-embedding. Suppose that
![]() $\mathcal {F}$
is an exact interpolation functor with the fundamental function
$\mathcal {F}$
is an exact interpolation functor with the fundamental function
![]() $\psi _{\mathcal {F}}$
, and let:
$\psi _{\mathcal {F}}$
, and let:
Then, for every
![]() $\xi = (\xi _\gamma )_{\gamma \in \Gamma }$
, one has:
$\xi = (\xi _\gamma )_{\gamma \in \Gamma }$
, one has:
where
![]() $K = e^2 \lambda \sqrt {2} \,\,\psi _{\mathcal {F}}(1, 1)$
.
$K = e^2 \lambda \sqrt {2} \,\,\psi _{\mathcal {F}}(1, 1)$
.
Proof. Fix
![]() $\xi =(\xi _\gamma ) \in \mathbb {C}^{\Gamma }$
. Since
$\xi =(\xi _\gamma ) \in \mathbb {C}^{\Gamma }$
. Since
![]() $\ell _1(\Gamma )$
has cotype
$\ell _1(\Gamma )$
has cotype
![]() $2$
with
$2$
with
![]() $C_2(\ell _1(\Gamma )\leq \sqrt {2}$
, it follows from Proposition 4.3 that:
$C_2(\ell _1(\Gamma )\leq \sqrt {2}$
, it follows from Proposition 4.3 that:
Now observe that for any finite sequence
![]() $(f_i)_{i=1}^N$
in
$(f_i)_{i=1}^N$
in
![]() $C_\Gamma $
, we have (where for a given
$C_\Gamma $
, we have (where for a given
![]() $g\in G$
, the Dirac functional
$g\in G$
, the Dirac functional
![]() $\delta _g\in B_{C(G)^{*}}$
is given by
$\delta _g\in B_{C(G)^{*}}$
is given by
![]() $\delta _g(f) :=f(g)$
for all
$\delta _g(f) :=f(g)$
for all
![]() $f\in C(G)$
):
$f\in C(G)$
):
 $$ \begin{align*} \sum_{i=1}^N \|M_{\xi}f_i\|_{\ell_2(\Gamma)}^2 & \leq \|\xi\|_\infty \int_{G} \sum_{i=1}^N |f_i(g)|^2\,d\nu \\ & \leq \|\xi\|_{\infty}\,\sup_{g \in G} \sum_{i=1}^N |\delta_g(f_i)|^2 \leq \|\xi\|_\infty\, \sup_{\|x^{*}\|_{C(G)^{*}} \leq 1} \sum_{i=1}^N |x^{*}(f_i)|^2. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^N \|M_{\xi}f_i\|_{\ell_2(\Gamma)}^2 & \leq \|\xi\|_\infty \int_{G} \sum_{i=1}^N |f_i(g)|^2\,d\nu \\ & \leq \|\xi\|_{\infty}\,\sup_{g \in G} \sum_{i=1}^N |\delta_g(f_i)|^2 \leq \|\xi\|_\infty\, \sup_{\|x^{*}\|_{C(G)^{*}} \leq 1} \sum_{i=1}^N |x^{*}(f_i)|^2. \end{align*} $$
This shows that
![]() $\pi _2(M_\xi \colon C_\Gamma \to \ell _2(\Gamma )) \leq \|\xi \|_\infty $
. Since
$\pi _2(M_\xi \colon C_\Gamma \to \ell _2(\Gamma )) \leq \|\xi \|_\infty $
. Since
![]() $\|\xi \|_\infty = \|M_\xi \colon C_\Gamma \to \ell _2(\Gamma )\| \leq \pi _2(M_\xi \colon C_\Gamma \to \ell _2(\Gamma ))$
, we get:
$\|\xi \|_\infty = \|M_\xi \colon C_\Gamma \to \ell _2(\Gamma )\| \leq \pi _2(M_\xi \colon C_\Gamma \to \ell _2(\Gamma ))$
, we get:
Applying Proposition 5.1, we conclude (by submultiplicativity of
![]() $\psi _{\mathcal {F}}$
) that:
$\psi _{\mathcal {F}}$
) that:
 $$ \begin{align*} \pi_2(M_\xi \colon C_\Gamma \to X) & \leq \psi_{\mathcal{F}}(1, 1) \,\, \psi_{\mathcal{F}}\big(\pi_2(M_\xi\colon C_\Gamma \to \ell_1(\Gamma)), \pi_2(M_\xi\colon C_\Gamma \to \ell_2(\Gamma)\big) \\ & \leq K\, \psi_{\mathcal{F}}\big(\sqrt{1 + \log N}, 1\big) \,\, \psi_{\mathcal{F}}\big(\|M_\xi\colon C_\Gamma \to \ell_1(\Gamma)\|, \|\xi\|_\infty\big). \end{align*} $$
$$ \begin{align*} \pi_2(M_\xi \colon C_\Gamma \to X) & \leq \psi_{\mathcal{F}}(1, 1) \,\, \psi_{\mathcal{F}}\big(\pi_2(M_\xi\colon C_\Gamma \to \ell_1(\Gamma)), \pi_2(M_\xi\colon C_\Gamma \to \ell_2(\Gamma)\big) \\ & \leq K\, \psi_{\mathcal{F}}\big(\sqrt{1 + \log N}, 1\big) \,\, \psi_{\mathcal{F}}\big(\|M_\xi\colon C_\Gamma \to \ell_1(\Gamma)\|, \|\xi\|_\infty\big). \end{align*} $$
This estimate combined with Lemma 2.1 yield the required statement.
In order to see a first consequence, we apply the preceding theorem to
![]() $G=\mathbb {T}^n$
and
$G=\mathbb {T}^n$
and
![]() $C_\Gamma = \mathcal {P}_{\leq m}(\mathbb {T}^n)$
with
$C_\Gamma = \mathcal {P}_{\leq m}(\mathbb {T}^n)$
with
![]() $\Gamma := \Lambda ^{\leq }(m,n)$
. For simplicity of notation, we for
$\Gamma := \Lambda ^{\leq }(m,n)$
. For simplicity of notation, we for
![]() $1\leq p \leq \infty $
write below
$1\leq p \leq \infty $
write below
![]() $\ell _p$
instead of
$\ell _p$
instead of
![]() $\ell _p(\Lambda ^{\leq }(m,n))$
.
$\ell _p(\Lambda ^{\leq }(m,n))$
.
Corollary 5.3. Let
![]() $\frac {1}{p_{\theta }} = (1-\theta ) + \frac {\theta }{2}$
for
$\frac {1}{p_{\theta }} = (1-\theta ) + \frac {\theta }{2}$
for
![]() $\theta \in (0, 1)$
. Then for every
$\theta \in (0, 1)$
. Then for every
![]() $\xi = (\xi _\gamma ) \in \mathbb {C}^{\Lambda ^{\leq }(m,n)}$
, one has:
$\xi = (\xi _\gamma ) \in \mathbb {C}^{\Lambda ^{\leq }(m,n)}$
, one has:
In particular, one has:
 $$ \begin{align*} \sup_{\|(\mu_\gamma)\|_{\ell_2} \leq 1}& \big\|(\mu_\gamma \xi_\gamma)\big\|_{\ell_{\frac{2m}{m+1}}} \\ & \leq 2 e^{2} \sqrt{2}\, \big(\sqrt{n(\log(1 + 20m)}\, \|M_\xi\colon \mathcal{P}_{\leq m}(\mathbb{T}^n) \to \ell_1\|\big)^{\frac{1}{m}} (\|\xi\|_{\infty})^{1- \frac{1}{m}}. \end{align*} $$
$$ \begin{align*} \sup_{\|(\mu_\gamma)\|_{\ell_2} \leq 1}& \big\|(\mu_\gamma \xi_\gamma)\big\|_{\ell_{\frac{2m}{m+1}}} \\ & \leq 2 e^{2} \sqrt{2}\, \big(\sqrt{n(\log(1 + 20m)}\, \|M_\xi\colon \mathcal{P}_{\leq m}(\mathbb{T}^n) \to \ell_1\|\big)^{\frac{1}{m}} (\|\xi\|_{\infty})^{1- \frac{1}{m}}. \end{align*} $$
Proof. It is well known that the complex method
![]() $\mathcal {F_\theta } := [\,\cdot \,]_{\theta }$
of interpolation has the fundamental function
$\mathcal {F_\theta } := [\,\cdot \,]_{\theta }$
of interpolation has the fundamental function
![]() $\psi _{F}(s, t) = s^{1-\theta }t^{\theta }$
for all
$\psi _{F}(s, t) = s^{1-\theta }t^{\theta }$
for all
![]() $s, t>0$
. Applying the well-known interpolation formula for couples of
$s, t>0$
. Applying the well-known interpolation formula for couples of
![]() $\ell _p$
-spaces, we get:
$\ell _p$
-spaces, we get:
Since by Bernstein’s result from (2.2) there exists a
![]() $2$
-embedding of
$2$
-embedding of
![]() $\mathcal {P}_{\leq m}(\mathbb { T}^n)$
into
$\mathcal {P}_{\leq m}(\mathbb { T}^n)$
into
![]() $\ell _{\infty }^N$
with
$\ell _{\infty }^N$
with
![]() $N = (1 + 20m)^n$
, Theorem 5.2 gives the first conclusion. To get the second assertion, we take
$N = (1 + 20m)^n$
, Theorem 5.2 gives the first conclusion. To get the second assertion, we take
![]() $\theta = 1- \frac {1}{m}$
.
$\theta = 1- \frac {1}{m}$
.
For another seemingly interesting consequence, we recall the definition of the abstract Lorentz space
![]() $\Lambda _{\varphi }(\vec {X})$
.
$\Lambda _{\varphi }(\vec {X})$
.
For a given function
![]() $\varphi \in \mathcal {Q}$
and Banach couple
$\varphi \in \mathcal {Q}$
and Banach couple
![]() $\vec {X}=(X_0, X_1)$
, the abstract Lorentz space
$\vec {X}=(X_0, X_1)$
, the abstract Lorentz space
![]() $\Lambda _{\varphi }(\vec {X})$
is defined to be the space of all
$\Lambda _{\varphi }(\vec {X})$
is defined to be the space of all
![]() $x\in X_0 + X_1$
, such that:
$x\in X_0 + X_1$
, such that:
where
![]() $x_{n}\in X_0\cap X_1$
and
$x_{n}\in X_0\cap X_1$
and
![]() $\sum _{n\in {\mathbb Z}}\, \varphi (\|x_{n}\|_{X_0}, \|x_{n}\|_{X_1}) <\infty $
. The norm on
$\sum _{n\in {\mathbb Z}}\, \varphi (\|x_{n}\|_{X_0}, \|x_{n}\|_{X_1}) <\infty $
. The norm on
![]() $\Lambda _{\varphi }(\vec {X})$
is defined by:
$\Lambda _{\varphi }(\vec {X})$
is defined by:
where the infimum is taken over all series described above. It is easily verified that
![]() $\Lambda _{\varphi }$
defines an exact interpolation functor.
$\Lambda _{\varphi }$
defines an exact interpolation functor.
Corollary 5.4. Under the notation and assumption of Theorem 5.2, we get for
![]() $\varphi :=\psi _{\mathcal {F}}$
:
$\varphi :=\psi _{\mathcal {F}}$
:
Proof. From Theorem 5.2, for any
![]() $\xi =(\xi _\gamma ) \in \mathbb {C}^{\Gamma }$
, we get that:
$\xi =(\xi _\gamma ) \in \mathbb {C}^{\Gamma }$
, we get that:
 $$ \begin{align*} \|D_{\xi}\colon \ell_2(\Gamma) &\to \mathcal{F}(\ell_1(\Gamma), \ell_2(\Gamma))\| \\ & \leq K \,\,\varphi\big(\sqrt{1 + \log N}, 1\big)\,\, \varphi(\|\xi\|_{\mathcal{M}(C_\Gamma, \ell_1(\Gamma))}, \|\xi\|_{\ell_{\infty}(\Gamma)}). \end{align*} $$
$$ \begin{align*} \|D_{\xi}\colon \ell_2(\Gamma) &\to \mathcal{F}(\ell_1(\Gamma), \ell_2(\Gamma))\| \\ & \leq K \,\,\varphi\big(\sqrt{1 + \log N}, 1\big)\,\, \varphi(\|\xi\|_{\mathcal{M}(C_\Gamma, \ell_1(\Gamma))}, \|\xi\|_{\ell_{\infty}(\Gamma)}). \end{align*} $$
By the construction of the abstract Lorentz space
![]() $\Lambda _{\varphi }$
, this completes the proof.
$\Lambda _{\varphi }$
, this completes the proof.
5.2 Variant II
Theorem 5.5. Let
![]() $\mathcal {F}$
be an exact interpolation functor with a fundamental function
$\mathcal {F}$
be an exact interpolation functor with a fundamental function
![]() $\psi _{\mathcal {F}}$
and for
$\psi _{\mathcal {F}}$
and for
![]() $m,n \in \mathbb {N}$
:
$m,n \in \mathbb {N}$
:
Then for every
![]() $\xi = (\xi _\alpha )_{\alpha \in \Lambda (m,n)}$
, one has:
$\xi = (\xi _\alpha )_{\alpha \in \Lambda (m,n)}$
, one has:
where
![]() $C(m) = e^2 2 \,\,\sqrt {2}\,\, \psi _{\mathcal {F}}(1, 1 )\, \,\psi _{\mathcal {F}}\big (\sqrt {\log (1 + 20 m)},1\big )$
.
$C(m) = e^2 2 \,\,\sqrt {2}\,\, \psi _{\mathcal {F}}(1, 1 )\, \,\psi _{\mathcal {F}}\big (\sqrt {\log (1 + 20 m)},1\big )$
.
In order to prove this result (see the end of this subsection), we apply Theorem 5.1 in combination with Proposition 4.3 and the following lemma.
Lemma 5.6. For each
![]() $m, n\in \mathbb {N}$
and for every
$m, n\in \mathbb {N}$
and for every
![]() $\xi \in \mathbb {C}^{\Lambda ^{\leq }(m, n)}$
,
$\xi \in \mathbb {C}^{\Lambda ^{\leq }(m, n)}$
,
In particular, if
![]() $\xi = \mathbf {1}$
,
$\xi = \mathbf {1}$
,
 $$ \begin{align*} \sqrt{1 + \frac{n-1}{m}} \leq \pi_2\big(M_\xi \colon \mathcal{P}_{\leq m}(\mathbb{T}^n) &\to \ell_{\frac{2m}{m+1}}(\Lambda^{\leq}(m, n)\big)\\ & = |\Lambda^{\leq}(m, n)|^{\frac{1}{2m}} \leq 2\sqrt{2e}\, \sqrt{1 + \frac{n-1}{m}}. \end{align*} $$
$$ \begin{align*} \sqrt{1 + \frac{n-1}{m}} \leq \pi_2\big(M_\xi \colon \mathcal{P}_{\leq m}(\mathbb{T}^n) &\to \ell_{\frac{2m}{m+1}}(\Lambda^{\leq}(m, n)\big)\\ & = |\Lambda^{\leq}(m, n)|^{\frac{1}{2m}} \leq 2\sqrt{2e}\, \sqrt{1 + \frac{n-1}{m}}. \end{align*} $$
Proof. We apply Lemma 4.1 in the case
![]() $G =\mathbb {T}^n$
with
$G =\mathbb {T}^n$
with
![]() $\Gamma =\Lambda ^{\leq }(m,n) \subset \widehat {G} = \mathbb {Z}^n$
and
$\Gamma =\Lambda ^{\leq }(m,n) \subset \widehat {G} = \mathbb {Z}^n$
and
![]() $F= \ell _{\frac {2m}{m+1}}(\Lambda ^{\leq }(m,n))$
. Clearly, for each
$F= \ell _{\frac {2m}{m+1}}(\Lambda ^{\leq }(m,n))$
. Clearly, for each
![]() $m, n\in \mathbb {N}$
, we have:
$m, n\in \mathbb {N}$
, we have:
 $$ \begin{align*} & \big\|\mathrm{{id}} \colon \ell_2(\Lambda^{\leq}(m, n)) \to \ell_{\frac{2m}{m+1}}(\Lambda^{\leq}(m, n))\big\| \\& =|\Lambda^{\leq}(m, n)|^{\frac{1}{2m}} = \bigg(\sum_{k=0}^m {k+n-1 \choose k}\bigg)^{\frac{1}{2m}} \leq (m+1)^{\frac{1}{2m}} {m+n-1 \choose m}^{\frac{1}{2m}} . \end{align*} $$
$$ \begin{align*} & \big\|\mathrm{{id}} \colon \ell_2(\Lambda^{\leq}(m, n)) \to \ell_{\frac{2m}{m+1}}(\Lambda^{\leq}(m, n))\big\| \\& =|\Lambda^{\leq}(m, n)|^{\frac{1}{2m}} = \bigg(\sum_{k=0}^m {k+n-1 \choose k}\bigg)^{\frac{1}{2m}} \leq (m+1)^{\frac{1}{2m}} {m+n-1 \choose m}^{\frac{1}{2m}} . \end{align*} $$
Applying the well-known quantitative version of Stirling’s formula yields:
 $$\begin{align*}{m+n-1 \choose m} \leq 2 e^m \Big(1 + \frac{n-1}{m}\Big)^m. \end{align*}$$
$$\begin{align*}{m+n-1 \choose m} \leq 2 e^m \Big(1 + \frac{n-1}{m}\Big)^m. \end{align*}$$
Now observe that, for any
![]() $x\geq y>z >0$
,
$x\geq y>z >0$
,
![]() $\frac {x-z}{y-z} \geq \frac {x}{y}$
and whence:
$\frac {x-z}{y-z} \geq \frac {x}{y}$
and whence:
 $$\begin{align*}{N \choose k} = \frac{N}{k}\,\frac{N-1}{k-1} \cdots \frac{N-k+1}{1} \geq \Big(\frac{N}{k}\Big)^k, \quad\, 1\leq k\leq N. \end{align*}$$
$$\begin{align*}{N \choose k} = \frac{N}{k}\,\frac{N-1}{k-1} \cdots \frac{N-k+1}{1} \geq \Big(\frac{N}{k}\Big)^k, \quad\, 1\leq k\leq N. \end{align*}$$
In consequence, we deduce that:
 $$\begin{align*}\sqrt{1 + \frac{n-1}{m}} \leq |\Lambda^{\leq}(m, n)|^{\frac{1}{2m}} \leq 2 \sqrt{2e}\, \sqrt{1 + \frac{n-1}{m}}, \end{align*}$$
$$\begin{align*}\sqrt{1 + \frac{n-1}{m}} \leq |\Lambda^{\leq}(m, n)|^{\frac{1}{2m}} \leq 2 \sqrt{2e}\, \sqrt{1 + \frac{n-1}{m}}, \end{align*}$$
and this gives the required estimates.
Finally, we are prepared to give the proof of Theorem 5.5.
Proof. (of Theorem 5.5)
Note that:
Since
![]() $\ell _1(\Lambda ^{\leq }(m,n)$
has cotype
$\ell _1(\Lambda ^{\leq }(m,n)$
has cotype
![]() $2$
with
$2$
with
![]() $C_2(\ell _1(\Lambda ^{\leq }(m,n))\leq \sqrt {2}$
, it follows from Proposition 4.3 and the embedding from (2.2) that:
$C_2(\ell _1(\Lambda ^{\leq }(m,n))\leq \sqrt {2}$
, it follows from Proposition 4.3 and the embedding from (2.2) that:
From Lemma 5.6 we know that:
Applying Theorem 5.1, we conclude (by submulitiplicativity of
![]() $\psi _{\mathcal {F}}$
) that with
$\psi _{\mathcal {F}}$
) that with
![]() $C=\psi _{\mathcal {F}}(1, 1)$
, it holds that:
$C=\psi _{\mathcal {F}}(1, 1)$
, it holds that:
 $$ \begin{align*} & \sup_{\|\mu\|_{\ell_2(\Lambda^{\leq}(m,n))}\leq 1} \|(\mu_{\gamma} \xi_\gamma)_{\gamma \in \Gamma}\|_F \\ & \leq C \psi_{\mathcal{F}}\big(\pi_2(M_\xi\colon \mathcal{P}_{\leq m}(\mathbb{T}^n) \to \ell_1(\Lambda^{\leq}(m,n))), \pi_2(M_\xi\colon \mathcal{P}_{\leq m}(\mathbb{T}^n)\to \ell_2(\Lambda^{\leq}(m,n))\big) \\ & \leq C \psi_{\mathcal{F}}\big(e^2 2 \,\sqrt{2}\, \sqrt{n\log(1 + 20 m)}\, \beta, 2 \sqrt{2e} \sqrt{n} \,\beta \big)\\ & \leq C e^2 2 \,\sqrt{2} \, \beta \, \sqrt{n}\,\psi_{\mathcal{F}}\big(\sqrt{\log(1 + 20 m)},1\big). \\[-36pt] \end{align*} $$
$$ \begin{align*} & \sup_{\|\mu\|_{\ell_2(\Lambda^{\leq}(m,n))}\leq 1} \|(\mu_{\gamma} \xi_\gamma)_{\gamma \in \Gamma}\|_F \\ & \leq C \psi_{\mathcal{F}}\big(\pi_2(M_\xi\colon \mathcal{P}_{\leq m}(\mathbb{T}^n) \to \ell_1(\Lambda^{\leq}(m,n))), \pi_2(M_\xi\colon \mathcal{P}_{\leq m}(\mathbb{T}^n)\to \ell_2(\Lambda^{\leq}(m,n))\big) \\ & \leq C \psi_{\mathcal{F}}\big(e^2 2 \,\sqrt{2}\, \sqrt{n\log(1 + 20 m)}\, \beta, 2 \sqrt{2e} \sqrt{n} \,\beta \big)\\ & \leq C e^2 2 \,\sqrt{2} \, \beta \, \sqrt{n}\,\psi_{\mathcal{F}}\big(\sqrt{\log(1 + 20 m)},1\big). \\[-36pt] \end{align*} $$
The following corollary ‘interpolates’ the estimates from Corollary 3.2 (
![]() $p=1$
) and Lemma 5.6 (
$p=1$
) and Lemma 5.6 (
![]() $p=2m/(m+1)$
).
$p=2m/(m+1)$
).
Corollary 5.7. For
![]() $m \in \mathbb {N}$
, let
$m \in \mathbb {N}$
, let
![]() $1 \leq p \leq \frac {2m}{m+1}$
. Then, for each
$1 \leq p \leq \frac {2m}{m+1}$
. Then, for each
![]() $n\in \mathbb {N}$
and every
$n\in \mathbb {N}$
and every
![]() $\xi =(\xi _\alpha )_{\alpha \in \Lambda ^{\leq }(m,n)}$
,
$\xi =(\xi _\alpha )_{\alpha \in \Lambda ^{\leq }(m,n)}$
,
 $$\begin{align*}\Big(\sum_{\alpha \in \Lambda^{\leq}(m,n)} |\xi_{\alpha}|^r\Big)^{1/r} \leq 2\sqrt{2}e^2 \, \sqrt{n} \sqrt{\log (1+20m)}^{\beta_m}\,\,\|M_\xi\colon \mathcal{P}_{\leq m}(\mathbb{T}^n)\to \ell_p(\Lambda^{\leq }(m,n))\|, \end{align*}$$
$$\begin{align*}\Big(\sum_{\alpha \in \Lambda^{\leq}(m,n)} |\xi_{\alpha}|^r\Big)^{1/r} \leq 2\sqrt{2}e^2 \, \sqrt{n} \sqrt{\log (1+20m)}^{\beta_m}\,\,\|M_\xi\colon \mathcal{P}_{\leq m}(\mathbb{T}^n)\to \ell_p(\Lambda^{\leq }(m,n))\|, \end{align*}$$
where
![]() $\frac {1}{r} = \frac {1}{p} -\frac {1}{2}$
and
$\frac {1}{r} = \frac {1}{p} -\frac {1}{2}$
and
![]() $ \beta _m = 1 - \frac {1-1/p}{1-\frac {m+1}{2m}}. $
$ \beta _m = 1 - \frac {1-1/p}{1-\frac {m+1}{2m}}. $
Proof. Define
![]() $\theta _m \in (0,1)$
by
$\theta _m \in (0,1)$
by
![]() $\frac {1}{p} = \frac {1-\theta _m}{1} +\frac {\theta _m}{\frac {2m}{m+1}}.$
Then
$\frac {1}{p} = \frac {1-\theta _m}{1} +\frac {\theta _m}{\frac {2m}{m+1}}.$
Then
![]() $1-\theta _m = \beta _m$
. Hence, by Theorem 5.5 and as in the proof of Corollary 5.3, it follows that for every
$1-\theta _m = \beta _m$
. Hence, by Theorem 5.5 and as in the proof of Corollary 5.3, it follows that for every
![]() $\xi = (\xi _\alpha )_{\alpha \in \Lambda ^{\leq }(m,n)}$
, we get:
$\xi = (\xi _\alpha )_{\alpha \in \Lambda ^{\leq }(m,n)}$
, we get:
 $$ \begin{align*} \Big(\sum_{\alpha \in \Lambda^{\leq}(m,n)} |\xi_{\alpha}|^r\Big)^{1/r} \leq \,C(m)\,\sqrt{n}\, \|M_{\xi}\colon \mathcal{P}_{\leq m}(\mathbb{T}^n) \to \ell_1(\Lambda^{\leq}(m,n))\| , \end{align*} $$
$$ \begin{align*} \Big(\sum_{\alpha \in \Lambda^{\leq}(m,n)} |\xi_{\alpha}|^r\Big)^{1/r} \leq \,C(m)\,\sqrt{n}\, \|M_{\xi}\colon \mathcal{P}_{\leq m}(\mathbb{T}^n) \to \ell_1(\Lambda^{\leq}(m,n))\| , \end{align*} $$
where
![]() $C(m) = 2 \sqrt {2}e^2 \,(\log (1 + 20 m))^{\beta _m}$
.
$C(m) = 2 \sqrt {2}e^2 \,(\log (1 + 20 m))^{\beta _m}$
.
6 Applications
6.1 Multipliers of analytic trigonometric polynonials
Recall from (2) the definition of
![]() $\mathcal {P}_{\leq m}(\mathbb {T}^n)$
, all trigonometric analytic polynomials of degree
$\mathcal {P}_{\leq m}(\mathbb {T}^n)$
, all trigonometric analytic polynomials of degree
![]() $\leq m$
on the n-dimensional torus
$\leq m$
on the n-dimensional torus
![]() $\mathbb {T}^n$
and its subspace
$\mathbb {T}^n$
and its subspace
![]() $\mathcal {P}_{=m}(\mathbb {T}^n)$
of all m-homogeneous polynomials.
$\mathcal {P}_{=m}(\mathbb {T}^n)$
of all m-homogeneous polynomials.
We also recall a definition, which we already touched on in the introduction, the Hardy space:
and its m-homogeneous part:
6.1.1 Sidon constants I
Let
![]() $1 \leq p < \infty $
. By
$1 \leq p < \infty $
. By
![]() $\chi _p\big ( \mathcal {P}_{\leq m}(\mathbb {T}^n) \big )$
, we denote the p-Sidon constant of
$\chi _p\big ( \mathcal {P}_{\leq m}(\mathbb {T}^n) \big )$
, we denote the p-Sidon constant of
![]() $\mathcal {P}_{\leq m}(\mathbb {T}^n) $
, that is, the best constant
$\mathcal {P}_{\leq m}(\mathbb {T}^n) $
, that is, the best constant
![]() $c>0$
, such that, for all polynomials
$c>0$
, such that, for all polynomials
![]() $f(z)= \sum _{\alpha \in \Lambda ^{\leq } (m,n)} \widehat {f}(\alpha )z^\alpha $
, we have:
$f(z)= \sum _{\alpha \in \Lambda ^{\leq } (m,n)} \widehat {f}(\alpha )z^\alpha $
, we have:
 $$\begin{align*}\Big(\sum_{\alpha \in \Lambda^{\leq } (m,n)} |\widehat{f}(\alpha)|^p\Big)^{\frac{1}{p}} \leq c\, \|f\|_\infty. \end{align*}$$
$$\begin{align*}\Big(\sum_{\alpha \in \Lambda^{\leq } (m,n)} |\widehat{f}(\alpha)|^p\Big)^{\frac{1}{p}} \leq c\, \|f\|_\infty. \end{align*}$$
Similarly, we define
![]() $\chi _p\big ( \mathcal {P}_{= m}(\mathbb {T}^n) \big )$
, but in this case, we only consider m-homogeneous trigonometric polynomials instead of all trigonometric polynomials of degree less than or equal to m. Since for every
$\chi _p\big ( \mathcal {P}_{= m}(\mathbb {T}^n) \big )$
, but in this case, we only consider m-homogeneous trigonometric polynomials instead of all trigonometric polynomials of degree less than or equal to m. Since for every
![]() $f\in \mathcal {P}_{\leq m}(\mathbb {T}^n)$
:
$f\in \mathcal {P}_{\leq m}(\mathbb {T}^n)$
:
 $$\begin{align*}\Big(\sum_{|\alpha| \leq m} |\widehat{f}(\alpha)|^2\Big)^{\frac{1}{2}} =\Big(\int_{\mathbb{T}^n} |f(z)|^2\,dz\Big)^{\frac{1}{2}} \leq \|f\|_\infty, \end{align*}$$
$$\begin{align*}\Big(\sum_{|\alpha| \leq m} |\widehat{f}(\alpha)|^2\Big)^{\frac{1}{2}} =\Big(\int_{\mathbb{T}^n} |f(z)|^2\,dz\Big)^{\frac{1}{2}} \leq \|f\|_\infty, \end{align*}$$
it follows that, for each
![]() $m,n \in \mathbb {N}$
,
$m,n \in \mathbb {N}$
,
Observe also that the Bohnenblust–Hille inequality (2.1) combined with Hölder’s inequality imply that there exists a constant
![]() $C>0$
, such that, for each
$C>0$
, such that, for each
![]() $m,n \in \mathbb {N}$
, we have:
$m,n \in \mathbb {N}$
, we have:
Theorem 6.1. Let
![]() $1 \leq p \leq \frac {2m}{m+1}$
and
$1 \leq p \leq \frac {2m}{m+1}$
and
![]() $\frac {1}{r}=\frac {1}{p} - \frac {1}{2}$
. Then there is a universal positive constant
$\frac {1}{r}=\frac {1}{p} - \frac {1}{2}$
. Then there is a universal positive constant
![]() $\gamma $
, such that, for each
$\gamma $
, such that, for each
![]() $m,n \in \mathbb {N}$
:
$m,n \in \mathbb {N}$
:
 $$\begin{align*}\frac{1}{\gamma^m}\Big( \frac{n}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} \leq \chi_p\big( \mathcal{P}_{=m}(\mathbb{T}^n) \big) \leq \chi_p\big( \mathcal{P}_{\leq m}(\mathbb{T}^n) \big) \leq \gamma^m \Big( \frac{n}{m}\Big)^{\frac{m}{r}-\frac{1}{2}}. \end{align*}$$
$$\begin{align*}\frac{1}{\gamma^m}\Big( \frac{n}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} \leq \chi_p\big( \mathcal{P}_{=m}(\mathbb{T}^n) \big) \leq \chi_p\big( \mathcal{P}_{\leq m}(\mathbb{T}^n) \big) \leq \gamma^m \Big( \frac{n}{m}\Big)^{\frac{m}{r}-\frac{1}{2}}. \end{align*}$$
Note that
![]() $\frac {m}{r}-\frac {1}{2} \ge 0$
whenever
$\frac {m}{r}-\frac {1}{2} \ge 0$
whenever
![]() $1 \leq p \leq \frac {2m}{m+1}$
and
$1 \leq p \leq \frac {2m}{m+1}$
and
![]() $\frac {1}{r}=\frac {1}{p} - \frac {1}{2}$
. Moreover, as it should be, we have that
$\frac {1}{r}=\frac {1}{p} - \frac {1}{2}$
. Moreover, as it should be, we have that
![]() $\frac {m}{r}-\frac {1}{2}=\frac {m-1}{2}$
for
$\frac {m}{r}-\frac {1}{2}=\frac {m-1}{2}$
for
![]() $p=1$
and
$p=1$
and
![]() $\frac {m}{r}-\frac {1}{2}= 0$
for
$\frac {m}{r}-\frac {1}{2}= 0$
for
![]() $p=\frac {2m}{m+1}$
.
$p=\frac {2m}{m+1}$
.
For the homogeneous case and
![]() $p=1$
, this result is proved in [Reference Defant, Frerick, Ortega-Cerdá, Ounäıes and Seip8] (see also [Reference Defant, García, Maestre and Sevilla Peris9, Theorem 9.10]) — the upper estimate is based on the hypercontractivity of the Bohnenblust–Hille inequality and the lower estimate on the Kahane–Salem–Zygmund inequality. Here, we deduce the upper inequality from the case
$p=1$
, this result is proved in [Reference Defant, Frerick, Ortega-Cerdá, Ounäıes and Seip8] (see also [Reference Defant, García, Maestre and Sevilla Peris9, Theorem 9.10]) — the upper estimate is based on the hypercontractivity of the Bohnenblust–Hille inequality and the lower estimate on the Kahane–Salem–Zygmund inequality. Here, we deduce the upper inequality from the case
![]() $p=1$
by applying the complex interpolation method and the lower estimate by the following independently interesting lemma based on Corollary 4.5.
$p=1$
by applying the complex interpolation method and the lower estimate by the following independently interesting lemma based on Corollary 4.5.
Lemma 6.2. Let
![]() $1 \leq p \leq \frac {2m}{m+1}$
and
$1 \leq p \leq \frac {2m}{m+1}$
and
![]() $z \in \mathbb {C}^n$
, and denote by
$z \in \mathbb {C}^n$
, and denote by
![]() $z^\ast $
the decreasing rearrangement of z. Then, for each
$z^\ast $
the decreasing rearrangement of z. Then, for each
![]() $m \in \mathbb {N}$
, one has:
$m \in \mathbb {N}$
, one has:
where
![]() $\frac {1}{r}=\frac {1}{p} - \frac {1}{2}$
and:
$\frac {1}{r}=\frac {1}{p} - \frac {1}{2}$
and:
Proof. From Corollary 4.5, we deduce that:
 $$ \begin{align*} (z^\ast_n)^{rm} \sum_{|\alpha |=m}1 & = \sum_{ |\alpha |=m} \big( (z_n^\ast)^{\alpha_1} \cdots (z_n^\ast))^{\alpha_n} \big)^r \\ & \leq \sum_{ |\alpha |=m} (z^\ast)^{r \alpha} \leq (2\sqrt{2}e^2)^r\, (n \log (1+20m))^{\frac{r}{2}}\,\|M_z\|^r. \end{align*} $$
$$ \begin{align*} (z^\ast_n)^{rm} \sum_{|\alpha |=m}1 & = \sum_{ |\alpha |=m} \big( (z_n^\ast)^{\alpha_1} \cdots (z_n^\ast))^{\alpha_n} \big)^r \\ & \leq \sum_{ |\alpha |=m} (z^\ast)^{r \alpha} \leq (2\sqrt{2}e^2)^r\, (n \log (1+20m))^{\frac{r}{2}}\,\|M_z\|^r. \end{align*} $$
Since
![]() $\operatorname {dim}\mathcal {P}_m(\mathbb {T}^n) = \binom {n+m-1}{m}$
, we get:
$\operatorname {dim}\mathcal {P}_m(\mathbb {T}^n) = \binom {n+m-1}{m}$
, we get:
 $$\begin{align*}(z^\ast_n)^{rm} \frac{n^m}{m!}\leq (z^\ast_n)^{rm} \binom{n+m-1}{m} \leq (2\sqrt{2}e^2)^r\,(n \log (1+20m))^{\frac{r}{2}}\, \|M_z\|^r, \end{align*}$$
$$\begin{align*}(z^\ast_n)^{rm} \frac{n^m}{m!}\leq (z^\ast_n)^{rm} \binom{n+m-1}{m} \leq (2\sqrt{2}e^2)^r\,(n \log (1+20m))^{\frac{r}{2}}\, \|M_z\|^r, \end{align*}$$
and the desired result follows by taking roots.
We are ready to give the proof of the theorem.
Proof. (of Theorem 6.1)
Lower bound: If
![]() $\pmb {1} = (1, \ldots ,1) \in \mathbb {C}^{\Lambda ^{=}(m,n)}$
, then by the definition we obtain:
$\pmb {1} = (1, \ldots ,1) \in \mathbb {C}^{\Lambda ^{=}(m,n)}$
, then by the definition we obtain:
Then, by Lemma 6.2:
and so:
 $$ \begin{align*} \frac{1}{\gamma^m}\Big( \frac{n}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} & \leq \frac{1}{2\sqrt{2}e^2m^{\frac{1}{2}} (1 + \log m)^{\frac{1}{2}}}\Big(\frac{n}{m}\Big)^{\frac{m}{r}-\frac{1}{2}}\\ & \leq \frac{m^{\frac{m}{r}-\frac{1}{2}}}{2\sqrt{2}e^2(m!)^{\frac{1}{r}} (1 + \log m)^{\frac{1}{2}}}\Big(\frac{n}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} \leq \chi_p\big( \mathcal{P}_{= m}(\mathbb{T}^n) \big). \end{align*} $$
$$ \begin{align*} \frac{1}{\gamma^m}\Big( \frac{n}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} & \leq \frac{1}{2\sqrt{2}e^2m^{\frac{1}{2}} (1 + \log m)^{\frac{1}{2}}}\Big(\frac{n}{m}\Big)^{\frac{m}{r}-\frac{1}{2}}\\ & \leq \frac{m^{\frac{m}{r}-\frac{1}{2}}}{2\sqrt{2}e^2(m!)^{\frac{1}{r}} (1 + \log m)^{\frac{1}{2}}}\Big(\frac{n}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} \leq \chi_p\big( \mathcal{P}_{= m}(\mathbb{T}^n) \big). \end{align*} $$
Upper bound: Define
![]() $0 \leq \theta \leq 1$
by:
$0 \leq \theta \leq 1$
by:
 $$\begin{align*}\frac{1}{p} = \frac{\theta}{1} + \frac{1-\theta}{\frac{2m}{m+1}}, \end{align*}$$
$$\begin{align*}\frac{1}{p} = \frac{\theta}{1} + \frac{1-\theta}{\frac{2m}{m+1}}, \end{align*}$$
then:
We know that:
and by (6.1):
Applying the complex interpolation method, we get:
and so the conclusion follows.
Why would a positive answer to Conjecture 4.6 not lead to a better lower bound? In this case, we, for
![]() $\frac {1}{s} = \frac {m}{m-1}\big (\frac {1}{p}-\frac {m+1}{2m}\big )$
, would get that:
$\frac {1}{s} = \frac {m}{m-1}\big (\frac {1}{p}-\frac {m+1}{2m}\big )$
, would get that:
 $$\begin{align*}\frac{1}{\gamma^m} \Big( \frac{n}{m} \Big)^{\frac{m}{s}-\frac{1}{s}} \leq \chi_p\big( \mathcal{P}_{= m}(\mathbb{T}^n) \big). \end{align*}$$
$$\begin{align*}\frac{1}{\gamma^m} \Big( \frac{n}{m} \Big)^{\frac{m}{s}-\frac{1}{s}} \leq \chi_p\big( \mathcal{P}_{= m}(\mathbb{T}^n) \big). \end{align*}$$
But
![]() $\frac {m}{s}-\frac {1}{s} = \frac {m}{r}-\frac {1}{2}$
, where, again,
$\frac {m}{s}-\frac {1}{s} = \frac {m}{r}-\frac {1}{2}$
, where, again,
![]() $\frac {1}{r}= \frac {1}{p}-\frac {1}{2}$
, and so we would not arrive at a contradiction.
$\frac {1}{r}= \frac {1}{p}-\frac {1}{2}$
, and so we would not arrive at a contradiction.
6.1.2 Bohr radii
Denote by
![]() $K_n$
the nth Bohr radius, that is the best
$K_n$
the nth Bohr radius, that is the best
![]() $0 < r \leq 1$
, such that, for every
$0 < r \leq 1$
, such that, for every
![]() $f\in H_{\infty }(\mathbb {T}^{\infty })$
, we have:
$f\in H_{\infty }(\mathbb {T}^{\infty })$
, we have:
 $$\begin{align*}\sum_{\alpha \in \mathbb{N}_0^{(\mathbb{N})}} |\widehat{f}(\alpha)|\,r^{|\alpha|} \leq \|f\|_\infty. \end{align*}$$
$$\begin{align*}\sum_{\alpha \in \mathbb{N}_0^{(\mathbb{N})}} |\widehat{f}(\alpha)|\,r^{|\alpha|} \leq \|f\|_\infty. \end{align*}$$
It is known that:
 $$ \begin{align} \lim_{n \to \infty} \frac{K_n}{\sqrt{\frac{\log n}{ n}}} =1\,; \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \frac{K_n}{\sqrt{\frac{\log n}{ n}}} =1\,; \end{align} $$
this was established in [Reference Bayart, Pellegrino and Seoane-Sepulveda2], extending an earlier result of [Reference Defant, Frerick, Ortega-Cerdá, Ounäıes and Seip8], which basically proved that the limit is between
![]() $1$
and
$1$
and
![]() $\sqrt {2}$
. For a detailed account on all this, see the monograph [Reference Defant, García, Maestre and Sevilla Peris9].
$\sqrt {2}$
. For a detailed account on all this, see the monograph [Reference Defant, García, Maestre and Sevilla Peris9].
The original proof of the lower estimate in (6.2) is based on the Kahane–Salem–Zygmund inequality (see, e.g. [Reference Defant, García, Maestre and Sevilla Peris9, Theorem 7.1]). Let us indicate an alternative argument based on Theorem 4.4. We have that for each
![]() $m\in \mathbb {N}$
:
$m\in \mathbb {N}$
:
where
![]() $K^m_n$
is defined like
$K^m_n$
is defined like
![]() $K_n$
, only taking into account functions from
$K_n$
, only taking into account functions from
![]() $H_m(\mathbb {T}^\infty )$
instead of all functions from
$H_m(\mathbb {T}^\infty )$
instead of all functions from
![]() $H_m(\mathbb {T}^\infty )$
. Then a simple reformulation shows that:
$H_m(\mathbb {T}^\infty )$
. Then a simple reformulation shows that:
 $$\begin{align*}K_n \leq K^m_n = \frac{1}{ \sqrt[m]{\chi(m,n)}}\, \end{align*}$$
$$\begin{align*}K_n \leq K^m_n = \frac{1}{ \sqrt[m]{\chi(m,n)}}\, \end{align*}$$
(see [Reference Defant, García, Maestre and Sevilla Peris9, (9.15)]). Using the lower estimate from Theorem 6.1 (which was proved with Kislyakov’s ideas), and following the proof given in [Reference Defant, García, Maestre and Sevilla Peris9, Theorem 8.22], we obtain an alternative approach to the upper bound in (6.2) without using the Kahane–Salem–Zygmund inequality.
6.1.3 Monomial convergence I
Let V be a subset of
![]() $H_\infty (\mathbb {T}^\infty )$
, then:
$H_\infty (\mathbb {T}^\infty )$
, then:
 $$\begin{align*}\operatorname{\mathrm{mon}} V := \bigg\{ z \in \mathbb{C}^{\mathbb{N}}\colon\, \, \sum_{\alpha \in \mathbb{N}_0^{(\mathbb{N})}} \vert \widehat{f}(\alpha) z^{\alpha} \vert < \infty \,\,\,\text{for all } f\in V \bigg\} \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{mon}} V := \bigg\{ z \in \mathbb{C}^{\mathbb{N}}\colon\, \, \sum_{\alpha \in \mathbb{N}_0^{(\mathbb{N})}} \vert \widehat{f}(\alpha) z^{\alpha} \vert < \infty \,\,\,\text{for all } f\in V \bigg\} \end{align*}$$
is called the set of monomial convergence of V. If V is a closed subspace of
![]() $H_\infty (\mathbb {T}^n)$
, then a simple closed graph argument shows that
$H_\infty (\mathbb {T}^n)$
, then a simple closed graph argument shows that
![]() $z \in \operatorname {\mathrm {mon}} V$
if and only if there is
$z \in \operatorname {\mathrm {mon}} V$
if and only if there is
![]() $C = C(z)>0$
, such that, for every
$C = C(z)>0$
, such that, for every
![]() $f \in V$
,
$f \in V$
,
 $$\begin{align*}\sum_{\alpha \in \mathbb{N}_0^{(\mathbb{N})}} |\widehat{f}(\alpha) z^\alpha| \leq C \|f\|_\infty. \end{align*}$$
$$\begin{align*}\sum_{\alpha \in \mathbb{N}_0^{(\mathbb{N})}} |\widehat{f}(\alpha) z^\alpha| \leq C \|f\|_\infty. \end{align*}$$
A sequence
![]() $\xi = (\xi _\alpha )_{\alpha \in \mathbb {N}_0^{(\mathbb {N})}}$
is said to be multiplicative whenever for all
$\xi = (\xi _\alpha )_{\alpha \in \mathbb {N}_0^{(\mathbb {N})}}$
is said to be multiplicative whenever for all
![]() $\alpha , \beta \in \mathbb {N}_0^{(\mathbb {N})}$
, we have
$\alpha , \beta \in \mathbb {N}_0^{(\mathbb {N})}$
, we have
![]() $\xi _{\alpha + \beta } = \xi _{\alpha } \xi _{\beta } $
. Equivalently,
$\xi _{\alpha + \beta } = \xi _{\alpha } \xi _{\beta } $
. Equivalently,
![]() $\xi $
is multiplicative if and only if there is
$\xi $
is multiplicative if and only if there is
![]() $z \in \mathbb {C}^{\mathbb {N}}$
, such that, for all
$z \in \mathbb {C}^{\mathbb {N}}$
, such that, for all
![]() $\alpha \in \mathbb {N}_0^{(\mathbb {N})}$
, we have
$\alpha \in \mathbb {N}_0^{(\mathbb {N})}$
, we have
![]() $\xi _\alpha = z^{\alpha }$
, for all
$\xi _\alpha = z^{\alpha }$
, for all
![]() $\alpha \in \mathbb {N}_0^{(\mathbb {N})}$
(if
$\alpha \in \mathbb {N}_0^{(\mathbb {N})}$
(if
![]() $\xi $
is multiplicative, then define
$\xi $
is multiplicative, then define
![]() $z_k = \xi _{e_k}$
for each
$z_k = \xi _{e_k}$
for each
![]() $k \in \mathbb {N}$
).
$k \in \mathbb {N}$
).
Remark 6.3. Let
![]() $V \subset H_\infty (\mathbb {T}^\infty )$
be a closed subspace. Then
$V \subset H_\infty (\mathbb {T}^\infty )$
be a closed subspace. Then
![]() $\operatorname {\mathrm {mon}} V$
equals the set of all multiplicative
$\operatorname {\mathrm {mon}} V$
equals the set of all multiplicative
![]() $\ell _1(\Gamma )$
-multipliers
$\ell _1(\Gamma )$
-multipliers
![]() $\xi = (\xi _\alpha )_{\alpha \in \mathbb {N}_0^{(\mathbb {N})}}$
for V, where:
$\xi = (\xi _\alpha )_{\alpha \in \mathbb {N}_0^{(\mathbb {N})}}$
for V, where:
 $$\begin{align*}\Gamma :=\bigcup_{f \in V} \operatorname{\mathrm{supp}} \widehat{f} \subset \mathbb{Z}^{(\mathbb{N})}. \end{align*}$$
$$\begin{align*}\Gamma :=\bigcup_{f \in V} \operatorname{\mathrm{supp}} \widehat{f} \subset \mathbb{Z}^{(\mathbb{N})}. \end{align*}$$
We refer to the monograph [Reference Defant, García, Maestre and Sevilla Peris9] for a detailed exposition on the sets of monomial convergence of
![]() $H_\infty (\mathbb {T}^\infty )$
and its closed subspace
$H_\infty (\mathbb {T}^\infty )$
and its closed subspace
![]() $H_\infty ^m(\mathbb {T}^\infty )$
(together with all its consequences for spaces of holomorphic functions in infinitely many variables and ordinary Dirichlet series). In particular, the following results from [Reference Bayart, Defant, Frerick, Maestre and Sevilla1] (see also [Reference Defant, García, Maestre and Sevilla Peris9, Theorems 10.1 and -10.15]) give two (almost) complete description of both sets.
$H_\infty ^m(\mathbb {T}^\infty )$
(together with all its consequences for spaces of holomorphic functions in infinitely many variables and ordinary Dirichlet series). In particular, the following results from [Reference Bayart, Defant, Frerick, Maestre and Sevilla1] (see also [Reference Defant, García, Maestre and Sevilla Peris9, Theorems 10.1 and -10.15]) give two (almost) complete description of both sets.
Theorem 6.4.
-
(i)
 $ \operatorname {\mathrm {mon}} H_\infty ^m(\mathbb {T}^\infty ) = \ell _{\frac {2m}{m-1}, \infty }$
for each
$ \operatorname {\mathrm {mon}} H_\infty ^m(\mathbb {T}^\infty ) = \ell _{\frac {2m}{m-1}, \infty }$
for each
 $m\in \mathbb {N}$
;
$m\in \mathbb {N}$
; -
(ii) For every
 $z \in \mathbb {C}^{\mathbb {N}}$
, the following two statements hold:
$z \in \mathbb {C}^{\mathbb {N}}$
, the following two statements hold:-
(a) If
 $\displaystyle \limsup _{n \to \infty } \frac {1}{\log n} \sum _{j=1}^{n} z^{* 2}_{j} < 1$
, then
$\displaystyle \limsup _{n \to \infty } \frac {1}{\log n} \sum _{j=1}^{n} z^{* 2}_{j} < 1$
, then
 $z \in \operatorname {\mathrm {mon}} H_\infty (\mathbb {T}^\infty )$
.
$z \in \operatorname {\mathrm {mon}} H_\infty (\mathbb {T}^\infty )$
. -
(b) If
 $z \in \operatorname {\mathrm {mon}} H_\infty (\mathbb {T}^\infty )$
, then
$z \in \operatorname {\mathrm {mon}} H_\infty (\mathbb {T}^\infty )$
, then
 $\displaystyle \limsup _{n \to \infty } \frac {1}{\log n} \sum _{j=1}^{n} z^{*2}_{j} \leq 1$
. Moreover, here, the converse implication is false.
$\displaystyle \limsup _{n \to \infty } \frac {1}{\log n} \sum _{j=1}^{n} z^{*2}_{j} \leq 1$
. Moreover, here, the converse implication is false.
-
In fact, the ‘lower inclusions’ for
![]() $\operatorname {\mathrm {mon}} H_\infty (\mathbb {T}^\infty )$
and
$\operatorname {\mathrm {mon}} H_\infty (\mathbb {T}^\infty )$
and
![]() $\operatorname {\mathrm {mon}} H_\infty ^m(\mathbb {T}^\infty )$
follow from the Kahane–Salem–Zygmund theorem. Alternatively, the following two proofs show that these lower inclusions also may be deduced from Theorem 4.4.
$\operatorname {\mathrm {mon}} H_\infty ^m(\mathbb {T}^\infty )$
follow from the Kahane–Salem–Zygmund theorem. Alternatively, the following two proofs show that these lower inclusions also may be deduced from Theorem 4.4.
Proof. (alternative proof of
 $\ell _{\frac {2m}{m-1}} \subset \operatorname {\mathrm {mon}} H_\infty ^m(\mathbb {T}^\infty )$
in Theorem 6.4)
$\ell _{\frac {2m}{m-1}} \subset \operatorname {\mathrm {mon}} H_\infty ^m(\mathbb {T}^\infty )$
in Theorem 6.4)
Fix
![]() $z \in \operatorname {\mathrm {mon}} H_\infty (\mathbb {T}^\infty )$
, and recall that then the decreasing rearrangement
$z \in \operatorname {\mathrm {mon}} H_\infty (\mathbb {T}^\infty )$
, and recall that then the decreasing rearrangement
![]() $z^\ast \in \operatorname {\mathrm {mon}} H_\infty (\mathbb {T}^\infty )$
(see [Reference Defant, García, Maestre and Sevilla Peris9, Remark 10.4]). Then:
$z^\ast \in \operatorname {\mathrm {mon}} H_\infty (\mathbb {T}^\infty )$
(see [Reference Defant, García, Maestre and Sevilla Peris9, Remark 10.4]). Then:
is bounded. Consequently, by Lemma 6.2, there is some universal constant
![]() $\gamma>0$
, such that, for each
$\gamma>0$
, such that, for each
![]() $m\in \mathbb {N}$
,
$m\in \mathbb {N}$
,
Taking the mth-rot, we conclude that:
and this completes the proof.
Proof. (alternative proof of
 $\mathrm {(2b)}$
in Theorem 6.4)
$\mathrm {(2b)}$
in Theorem 6.4)
With the closed graph argument from the preceding proof and Theorem 3.2, we see that for some constant
![]() $\gamma>0$
and each
$\gamma>0$
and each
![]() $m,n\in \mathbb {N}$
, we have:
$m,n\in \mathbb {N}$
, we have:
 $$\begin{align*}\Big(\sum_{\substack{\alpha \in \mathbb{ N}_0^{n}\\ |\alpha |=m}} |(z^\ast)^{\alpha}|^2\Big)^{\frac{1}{2}} \leq \gamma\,\sqrt{ n \log m}. \end{align*}$$
$$\begin{align*}\Big(\sum_{\substack{\alpha \in \mathbb{ N}_0^{n}\\ |\alpha |=m}} |(z^\ast)^{\alpha}|^2\Big)^{\frac{1}{2}} \leq \gamma\,\sqrt{ n \log m}. \end{align*}$$
Then the proof finishes exactly as in [Reference Defant, García, Maestre and Sevilla Peris9, Section 10.5.1].
6.1.4 Bohr–Bohnenblust–Hille theorem
Referring to a couple of results, which were worked out in the recent monograph [Reference Defant, García, Maestre and Sevilla Peris9], we intend to show that our alternative approach to Theorem 6.4.(ii.b) leads to an alternative solution of Bohr’s famous absolute convergence problem on ordinary Dirichlet series.
This problem asked for the largest possible width S of the strip in the complex plane on which an ordinary Dirichlet series
![]() $D=\sum a_n n^{-s}$
converges uniformly but not absolutely (see [Reference Defant, García, Maestre and Sevilla Peris9, Section 1]).
$D=\sum a_n n^{-s}$
converges uniformly but not absolutely (see [Reference Defant, García, Maestre and Sevilla Peris9, Section 1]).
Bohr, himself, established the upper estimate
![]() $S \leq ~1/2$
(see [Reference Defant, García, Maestre and Sevilla Peris9, Proposition 1.10]), but he was not able to decide whether this upper bound is optimal. A nontrivial reformulation (still due to Bohr, see [Reference Defant, García, Maestre and Sevilla Peris9, Proposition 1.24]) shows that:
$S \leq ~1/2$
(see [Reference Defant, García, Maestre and Sevilla Peris9, Proposition 1.10]), but he was not able to decide whether this upper bound is optimal. A nontrivial reformulation (still due to Bohr, see [Reference Defant, García, Maestre and Sevilla Peris9, Proposition 1.24]) shows that:
where
![]() $\mathcal {H}_\infty $
denotes the Banach space of all Dirichlet series D, which on the positive half plane converge pointwise to a bounded (and then necessarily holomorphic) function and
$\mathcal {H}_\infty $
denotes the Banach space of all Dirichlet series D, which on the positive half plane converge pointwise to a bounded (and then necessarily holomorphic) function and
![]() $\sigma _a(D) \in \mathbb {R}$
defines the abscissa of absolute convergence of D.
$\sigma _a(D) \in \mathbb {R}$
defines the abscissa of absolute convergence of D.
On the other hand,
that is, there is an isometric linear bijection between both Banach spaces preserving Dirichlet and Fourier coefficients. More precisely, if this bijection identifies
![]() $f\in H_{\infty }(\mathbb {T}^{\infty })$
and
$f\in H_{\infty }(\mathbb {T}^{\infty })$
and
![]() $D = \sum a_n n^{-s} \in \mathcal {H}_\infty $
, then
$D = \sum a_n n^{-s} \in \mathcal {H}_\infty $
, then
![]() $a_n = \widehat {f}(\alpha )$
, whenever
$a_n = \widehat {f}(\alpha )$
, whenever
![]() $n = \mathfrak {p}^\alpha $
(here,
$n = \mathfrak {p}^\alpha $
(here,
![]() $\mathfrak {p} = (p_n)$
stands for the sequence of primes (see [Reference Defant, García, Maestre and Sevilla Peris9, Corollary 5.3]). Then this fact combined with (6.3) show that:
$\mathfrak {p} = (p_n)$
stands for the sequence of primes (see [Reference Defant, García, Maestre and Sevilla Peris9, Corollary 5.3]). Then this fact combined with (6.3) show that:
(see [Reference Defant, García, Maestre and Sevilla Peris9, (10.5)]). As a consequence, we see that Theorem 6.4.
![]() $(iib)$
, for which we gave an alternative proof using Kislyakov’s ideas condensed in Theorem 4.4, immediately proves that
$(iib)$
, for which we gave an alternative proof using Kislyakov’s ideas condensed in Theorem 4.4, immediately proves that
![]() $S\ge 1/2$
.
$S\ge 1/2$
.
So, all in all, we arrive at a new proof of the so-called Bohr–Bohnenblust–Hille theorem:
![]() $S= \frac {1}{2}$
, which, in fact, is in the very centre of the discussion in the monograph [Reference Defant, García, Maestre and Sevilla Peris9] (for the highly nontrivial original proof due to Bohnenblust and Hille from 1931, see [Reference Defant, García, Maestre and Sevilla Peris9, Section 2]). We finally remark that this monograph also contains a couple of other proofs — none of them being trivial.
$S= \frac {1}{2}$
, which, in fact, is in the very centre of the discussion in the monograph [Reference Defant, García, Maestre and Sevilla Peris9] (for the highly nontrivial original proof due to Bohnenblust and Hille from 1931, see [Reference Defant, García, Maestre and Sevilla Peris9, Section 2]). We finally remark that this monograph also contains a couple of other proofs — none of them being trivial.
6.2 Multipliers of functions on Boolean cubes
For
![]() $N \in \mathbb {N}$
, let
$N \in \mathbb {N}$
, let
![]() $\mathcal {B}_N$
be the set of all functions
$\mathcal {B}_N$
be the set of all functions
![]() $f:\{-1,1\}^{N} \rightarrow \mathbb { R}$
. Recall for
$f:\{-1,1\}^{N} \rightarrow \mathbb { R}$
. Recall for
![]() $f\in \mathcal {B}_N$
, the expectation is given by:
$f\in \mathcal {B}_N$
, the expectation is given by:
 $$\begin{align*}\mathbb{E}\big[ f \big] := \frac{1}{2^{N}} \sum_{x \in \{-1,1\}^{N}}{f(x)}. \end{align*}$$
$$\begin{align*}\mathbb{E}\big[ f \big] := \frac{1}{2^{N}} \sum_{x \in \{-1,1\}^{N}}{f(x)}. \end{align*}$$
The dual group of
![]() $\{-1,1\}^{N}$
actually consists of the set of all Walsh functions
$\{-1,1\}^{N}$
actually consists of the set of all Walsh functions
![]() $\chi _{S}$
for
$\chi _{S}$
for
![]() $S \subset [N]$
, which allows to associate to each such
$S \subset [N]$
, which allows to associate to each such
![]() $f \in \mathcal {B}_N$
its Fourier-Walsh expansion:
$f \in \mathcal {B}_N$
its Fourier-Walsh expansion:
 $$ \begin{align} f(x) = \sum_{S \subset [N]}{\widehat{f}(S) \, x^S}\, , \hspace{3mm} x \in \{-1, 1\}^{N}, \end{align} $$
$$ \begin{align} f(x) = \sum_{S \subset [N]}{\widehat{f}(S) \, x^S}\, , \hspace{3mm} x \in \{-1, 1\}^{N}, \end{align} $$
where
![]() $x^{S}:= \chi _{S}(x):= \prod _{n \in S}x_{n}$
are the Walsh functions and the coefficients are given by
$x^{S}:= \chi _{S}(x):= \prod _{n \in S}x_{n}$
are the Walsh functions and the coefficients are given by
![]() $\widehat {f}(S) = \mathbb {E}[ f \chi _{S} ]$
. Thereby, a nonzero function f of degree d satisfies that
$\widehat {f}(S) = \mathbb {E}[ f \chi _{S} ]$
. Thereby, a nonzero function f of degree d satisfies that
![]() $\widehat {f}(S) = 0$
provided
$\widehat {f}(S) = 0$
provided
![]() $|S|> d$
. We say that f is m-homogeneous whenever
$|S|> d$
. We say that f is m-homogeneous whenever
![]() $\widehat {f}(S) = 0$
provided
$\widehat {f}(S) = 0$
provided
![]() $|S| \neq m$
.
$|S| \neq m$
.
Given
![]() $m,d \in \mathbb {N}$
with
$m,d \in \mathbb {N}$
with
![]() $m,d \leq N$
, we write
$m,d \leq N$
, we write
![]() $\mathcal {B}_N^{=m}$
for all m-homogeneous functions in
$\mathcal {B}_N^{=m}$
for all m-homogeneous functions in
![]() $\mathcal {B}_N$
and
$\mathcal {B}_N$
and
![]() $\mathcal {B}_N^{\leq d}$
for all functions of degree
$\mathcal {B}_N^{\leq d}$
for all functions of degree
![]() $\leq d$
. Moreover, we define:
$\leq d$
. Moreover, we define:
Similar to (2.1), we have the following ‘hypercontractive’ Bohnenblust–Hille inequality for functions on the Boolean cube from [Reference Defant, Mastyło and Pérez12]: There is a universal constant
![]() $C>1$
, such that, for each
$C>1$
, such that, for each
![]() $d, N\in \mathbb {N}$
and for every
$d, N\in \mathbb {N}$
and for every
![]() $f\in \mathcal {B}_N^{\leq d}$
, we have:
$f\in \mathcal {B}_N^{\leq d}$
, we have:
 $$ \begin{align} \Big(\sum_{S \subset [N]\colon |S|\leq d} |\widehat{f}(S)|^{\frac{2m}{m+1}}\Big)^{\frac{m+1}{2m}} \leq C^{\sqrt{m \log m}} \|f\|_\infty. \end{align} $$
$$ \begin{align} \Big(\sum_{S \subset [N]\colon |S|\leq d} |\widehat{f}(S)|^{\frac{2m}{m+1}}\Big)^{\frac{m+1}{2m}} \leq C^{\sqrt{m \log m}} \|f\|_\infty. \end{align} $$
6.2.1 Multipliers
We start with variants of Theorem 4.4 and Corollary 3.2 for functions on the Boolean cubes.
Theorem 6.5. Assume that
![]() $1 \leq p \leq 2$
and
$1 \leq p \leq 2$
and
![]() $d,N \in \mathbb {N}$
with
$d,N \in \mathbb {N}$
with
![]() $d \leq N$
. Define
$d \leq N$
. Define
![]() $1 \leq r < \infty $
by
$1 \leq r < \infty $
by
![]() $\frac {1}{r}=\frac {1}{p}-\frac {1}{2}$
. Then,
$\frac {1}{r}=\frac {1}{p}-\frac {1}{2}$
. Then,
-
(i) for every
 $ \xi =(\xi _S)_{S \subset [N]}$
,
$ \xi =(\xi _S)_{S \subset [N]}$
,  $$ \begin{align*} \frac{1}{\sqrt{1 +N \log 2}}\Big(\sum_{S \subset [N]} |\xi_S|^r\Big)^{\frac{1}{r}} \leq 2\sqrt{2} e^2 \big\|M_\xi\colon \mathcal{B}_N \to \ell_p(\{S \colon S \subset [N] \})\big\|. \end{align*} $$
$$ \begin{align*} \frac{1}{\sqrt{1 +N \log 2}}\Big(\sum_{S \subset [N]} |\xi_S|^r\Big)^{\frac{1}{r}} \leq 2\sqrt{2} e^2 \big\|M_\xi\colon \mathcal{B}_N \to \ell_p(\{S \colon S \subset [N] \})\big\|. \end{align*} $$
-
(ii) for every
 $\xi =(\xi _S)_{S \subset [N], |S|\leq d}$
, Moreover, in the homogeneous case
$\xi =(\xi _S)_{S \subset [N], |S|\leq d}$
, Moreover, in the homogeneous case $$ \begin{align*} \frac{1}{\sqrt{1+N\log(1+20 d)}}&\Big(\sum_{_{S \subset [N], |S|\leq d}} |\xi_S|^r\Big)^{\frac{1}{r}} \\ & \leq 2\sqrt{2} e^2 (1 +\sqrt{2})^d \big\|M_\xi\colon \mathcal{B}^{\leq d}_N \to \ell_p(\{S \colon |S|\leq d \})\big\|. \end{align*} $$
$$ \begin{align*} \frac{1}{\sqrt{1+N\log(1+20 d)}}&\Big(\sum_{_{S \subset [N], |S|\leq d}} |\xi_S|^r\Big)^{\frac{1}{r}} \\ & \leq 2\sqrt{2} e^2 (1 +\sqrt{2})^d \big\|M_\xi\colon \mathcal{B}^{\leq d}_N \to \ell_p(\{S \colon |S|\leq d \})\big\|. \end{align*} $$
 $\xi =(\xi _S)_{S \subset [N], |S|= d}$
, we may replace the constant on the right side by
$\xi =(\xi _S)_{S \subset [N], |S|= d}$
, we may replace the constant on the right side by
 $2\sqrt {2} e^2 2^{d-1}$
.
$2\sqrt {2} e^2 2^{d-1}$
.
Proof. For the proof of both statements, we use the fact that
![]() $C_2(\ell _p(\Gamma )) \leq \sqrt {2}$
for
$C_2(\ell _p(\Gamma )) \leq \sqrt {2}$
for
![]() $1 \leq p \leq 2$
. Consider then for the proof of
$1 \leq p \leq 2$
. Consider then for the proof of
![]() $\mathrm {(i)}$
the canonical isometric embedding:
$\mathrm {(i)}$
the canonical isometric embedding:
Then the conclusion is immediate from Theorem 4.4. The proof of
![]() $\mathrm {(ii)}$
is slightly more involved: Denote by
$\mathrm {(ii)}$
is slightly more involved: Denote by
![]() $\mathcal {P}_{\leq d}([-1,1]^N)$
the space of all real polynomials
$\mathcal {P}_{\leq d}([-1,1]^N)$
the space of all real polynomials
![]() $f(x)=\sum _{\alpha \in \mathbb {N}_0^n: |\alpha |\leq d} c_\alpha x^\alpha , \, x \in \mathbb {R}^N$
, and endow it with the supremum norm on the N-dimensional cube
$f(x)=\sum _{\alpha \in \mathbb {N}_0^n: |\alpha |\leq d} c_\alpha x^\alpha , \, x \in \mathbb {R}^N$
, and endow it with the supremum norm on the N-dimensional cube
![]() $[0,1]^N$
. Since every
$[0,1]^N$
. Since every
![]() $f \in \mathcal {B}_N$
can be viewed as a tetrahedral polynomial in
$f \in \mathcal {B}_N$
can be viewed as a tetrahedral polynomial in
![]() $ \mathcal {P}_{\leq d}([-1,1]^N) $
with equal norm, the canonical embedding:
$ \mathcal {P}_{\leq d}([-1,1]^N) $
with equal norm, the canonical embedding:
is isometric. Next we look at the canonical embedding:
which by a result of Klimek [Reference Klimek16] is an
![]() $(1 + \sqrt {2})^d$
-embedding, and, finally, we recall that by (2.2), there is a
$(1 + \sqrt {2})^d$
-embedding, and, finally, we recall that by (2.2), there is a
![]() $2$
-embedding:
$2$
-embedding:
where
![]() $M = (1 + 20 m)^N$
. Then the conclusion again follows from Theorem 4.4. In the d-homogeneous case, we replace Klimek’s with a result of Visser [Reference Visser21], which states that the canonical map from
$M = (1 + 20 m)^N$
. Then the conclusion again follows from Theorem 4.4. In the d-homogeneous case, we replace Klimek’s with a result of Visser [Reference Visser21], which states that the canonical map from
![]() $\mathcal {P}_{= d}([-1,1]^N)$
into
$\mathcal {P}_{= d}([-1,1]^N)$
into
![]() $\mathcal {P}_{=d}(\mathbb {T}^N)$
is a
$\mathcal {P}_{=d}(\mathbb {T}^N)$
is a
![]() $2^{d-1}$
- embedding. This completes the proof.
$2^{d-1}$
- embedding. This completes the proof.
6.2.2 Sidon constants II
The preceding theorem is used to obtain the following analog of Theorem 6.1.
Theorem 6.6. Let
![]() $1\leq p \leq \frac {2m}{m+1}$
and
$1\leq p \leq \frac {2m}{m+1}$
and
![]() $r>0$
with
$r>0$
with
![]() $\frac {1}{r}=\frac {1}{p} - \frac {1}{2}$
. Then, there is a universal constant
$\frac {1}{r}=\frac {1}{p} - \frac {1}{2}$
. Then, there is a universal constant
![]() $\gamma \geq 1$
, such that, for each positive integer
$\gamma \geq 1$
, such that, for each positive integer
![]() $m \leq N$
:
$m \leq N$
:
 $$\begin{align*}\frac{1}{\gamma^m}\Big(\frac{N}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} \leq \chi_p\big( \mathcal{B}_{N}^{=m} \big) \leq \chi_p\big( \mathcal{B}_{N}^{\leq m} \big) \leq \gamma^m \Big( \frac{N}{m}\Big)^{\frac{m}{r}-\frac{1}{2}}. \end{align*}$$
$$\begin{align*}\frac{1}{\gamma^m}\Big(\frac{N}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} \leq \chi_p\big( \mathcal{B}_{N}^{=m} \big) \leq \chi_p\big( \mathcal{B}_{N}^{\leq m} \big) \leq \gamma^m \Big( \frac{N}{m}\Big)^{\frac{m}{r}-\frac{1}{2}}. \end{align*}$$
Note that in a similar fashion as\ in Section 6.1.1, for each
![]() $m\leq N$
, one has:
$m\leq N$
, one has:
and, combining the Bohnenblust–Hille inequality for functions on the Boolen cube from (6.5) with Hölder’s inequality, there exists a constant
![]() $\gamma \geq 1$
, such that:
$\gamma \geq 1$
, such that:
We prepare the proof of the preceding theorem with a lemma similar to Lemma 6.2.
Lemma 6.7. Let
![]() $1 \leq p \leq \frac {2m}{m+1}$
and
$1 \leq p \leq \frac {2m}{m+1}$
and
![]() $z \in \mathbb {C}^N$
, and denote by
$z \in \mathbb {C}^N$
, and denote by
![]() $z^\ast $
the decreasing rearrangement of z. Then, for each
$z^\ast $
the decreasing rearrangement of z. Then, for each
![]() $m \leq N$
, the following estimate holds:
$m \leq N$
, the following estimate holds:
where
![]() $\frac {1}{r}=\frac {1}{p} - \frac {1}{2}$
and
$\frac {1}{r}=\frac {1}{p} - \frac {1}{2}$
and
![]() $M_z \colon \mathcal {B}_{N}^{= m} \to \ell _p(\{S\colon |S|= m\})$
is given by:
$M_z \colon \mathcal {B}_{N}^{= m} \to \ell _p(\{S\colon |S|= m\})$
is given by:
Proof. From Theorem 6.5, we get:
 $$ \begin{align*} (z^\ast_N)^{rm}&\sum_{ S \subset [N], |S |=m} 1 = \sum_{ S\subset [N], |S |=m} \big( (z_N^\ast)\ldots (z_N^\ast) \big)^r \\ & \leq \sum_{ S \subset [N], |S |=m} \big((z^\ast)^{S}\big)^{r} \leq (4e^2 2^{m-1})^r\, \big(1+N\log(1+20 m)\big)^{\frac{r}{2}}\,\|M_z\|^r. \end{align*} $$
$$ \begin{align*} (z^\ast_N)^{rm}&\sum_{ S \subset [N], |S |=m} 1 = \sum_{ S\subset [N], |S |=m} \big( (z_N^\ast)\ldots (z_N^\ast) \big)^r \\ & \leq \sum_{ S \subset [N], |S |=m} \big((z^\ast)^{S}\big)^{r} \leq (4e^2 2^{m-1})^r\, \big(1+N\log(1+20 m)\big)^{\frac{r}{2}}\,\|M_z\|^r. \end{align*} $$
This yields:
 $$ \begin{align*} (z^\ast_N)^{rm} \frac{N^m}{m!} \leq (z^\ast_N)^{rm} \binom{N}{m} \leq (4\sqrt{2}e^2 2^{m-1})^r\, \big(N\log(1+20 m)\big)^{\frac{r}{2}}\,\|M_z\|^r, \end{align*} $$
$$ \begin{align*} (z^\ast_N)^{rm} \frac{N^m}{m!} \leq (z^\ast_N)^{rm} \binom{N}{m} \leq (4\sqrt{2}e^2 2^{m-1})^r\, \big(N\log(1+20 m)\big)^{\frac{r}{2}}\,\|M_z\|^r, \end{align*} $$
as required.
Proof. (of Theorem 6.6)
Lower bound: For
![]() $\pmb {1} = (1, \ldots ,1) \in \mathbb {C}^{|\{S\colon |S|=m\}|}$
, we by definition have:
$\pmb {1} = (1, \ldots ,1) \in \mathbb {C}^{|\{S\colon |S|=m\}|}$
, we by definition have:
Then the conclusion follows if we, exactly as in Lemma 6.2, apply Lemma 6.7 to
![]() $z =\pmb {1}$
. Upper bound: Take
$z =\pmb {1}$
. Upper bound: Take
![]() $f \in \mathcal {B}^{\leq m}_N$
, and interpret it as a polynomial
$f \in \mathcal {B}^{\leq m}_N$
, and interpret it as a polynomial
![]() $F \in \mathcal {P}_{\leq m}(\mathbb {T}^N)$
. Then we know from Theorem 6.1 that:
$F \in \mathcal {P}_{\leq m}(\mathbb {T}^N)$
. Then we know from Theorem 6.1 that:
 $$ \begin{align*} \sum_{|S|\leq m} |\widehat{f}(S)| \leq \gamma^m \Big( \frac{N}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} \|F\|_{\mathcal{P}_{\leq m}(\mathbb{T}^N)}\leq \gamma^m (1 + \sqrt{2})^m \Big( \frac{N}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} \|f\|_{\mathcal{B}^{\leq m}_N}, \end{align*} $$
$$ \begin{align*} \sum_{|S|\leq m} |\widehat{f}(S)| \leq \gamma^m \Big( \frac{N}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} \|F\|_{\mathcal{P}_{\leq m}(\mathbb{T}^N)}\leq \gamma^m (1 + \sqrt{2})^m \Big( \frac{N}{m}\Big)^{\frac{m}{r}-\frac{1}{2}} \|f\|_{\mathcal{B}^{\leq m}_N}, \end{align*} $$
where the very last estimate, again, follows from a result of Klimek in [Reference Klimek16].
6.2.3 Monomial convergence II
Given
![]() $V \subset \mathcal {B}$
, we define the set of monomial convergence of V by:
$V \subset \mathcal {B}$
, we define the set of monomial convergence of V by:
 $$\begin{align*}\operatorname{\mathrm{mon}}(V) := \Big\{x \in \mathbb{ R}^{\mathbb{ N}}\colon\,\ \exists C> 0 \,\,\forall f \in V: \hspace{3mm} {\sum_{S\subset [N]}{|\widehat{f}(S) x^{S}|} \leq C \, \| f\|_{\infty}} \Big\}, \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{mon}}(V) := \Big\{x \in \mathbb{ R}^{\mathbb{ N}}\colon\,\ \exists C> 0 \,\,\forall f \in V: \hspace{3mm} {\sum_{S\subset [N]}{|\widehat{f}(S) x^{S}|} \leq C \, \| f\|_{\infty}} \Big\}, \end{align*}$$
where recall that
![]() $x^S := \prod _{n \in S}{x_{n}}$
for each
$x^S := \prod _{n \in S}{x_{n}}$
for each
![]() $S \subset [N]$
and for all
$S \subset [N]$
and for all
![]() $x \in \mathbb { R}^{\mathbb { N}}$
. Let us denote by
$x \in \mathbb { R}^{\mathbb { N}}$
. Let us denote by
![]() $S \subset _{fin} \mathbb {N}$
the fact that S is a finite subset of
$S \subset _{fin} \mathbb {N}$
the fact that S is a finite subset of
![]() $\mathbb {N}$
. We say that a real sequence
$\mathbb {N}$
. We say that a real sequence
![]() $(\xi _S)_{S\subset _{fin} \mathbb {N}}$
is multiplicative if:
$(\xi _S)_{S\subset _{fin} \mathbb {N}}$
is multiplicative if:
Note that
![]() $(\xi _S)_{S\subset _{fin} \mathbb {N}}$
is multiplicative if and only if there exists
$(\xi _S)_{S\subset _{fin} \mathbb {N}}$
is multiplicative if and only if there exists
![]() $x \in \mathbb { R}^{\mathbb { N}}$
, such that for all
$x \in \mathbb { R}^{\mathbb { N}}$
, such that for all
![]() $S \subset _{fin} \mathbb {N}$
, we have
$S \subset _{fin} \mathbb {N}$
, we have
![]() $x^{S} = \xi _S$
. Hence,
$x^{S} = \xi _S$
. Hence,
![]() $\operatorname {\mathrm {mon}}(V) $
consists exactly of all multiplicative
$\operatorname {\mathrm {mon}}(V) $
consists exactly of all multiplicative
![]() $\ell _1(\{S\colon S \subset _{fin} \mathbb {N}\})$
-multipliers of V.
$\ell _1(\{S\colon S \subset _{fin} \mathbb {N}\})$
-multipliers of V.
Here are some basic properties of
![]() $\operatorname {\mathrm {mon}} (\mathcal {B})$
.
$\operatorname {\mathrm {mon}} (\mathcal {B})$
.
Proposition 6.8. Let
![]() $x \in \operatorname {\mathrm {mon}} (\mathcal {B})$
and
$x \in \operatorname {\mathrm {mon}} (\mathcal {B})$
and
![]() $y \in \mathbb { R}^{\mathbb { N}}$
. Then, each of the following conditions yields that
$y \in \mathbb { R}^{\mathbb { N}}$
. Then, each of the following conditions yields that
![]() $y\in \operatorname {\mathrm {mon}} (\mathcal {B})$
:
$y\in \operatorname {\mathrm {mon}} (\mathcal {B})$
:
-
(i) y differs from x in a finite number of entries;
-
(ii) y is a permutation of x;
-
(iii)
 $|y_{n}| \leq |x_{n}|$
for each
$|y_{n}| \leq |x_{n}|$
for each
 $n \in \mathbb { N}$
.
$n \in \mathbb { N}$
.
Proof. To prove the sufficiency of (i), it is enough to assume that y differs from x in one entry,
![]() $x_{n} = y_{n}$
for each
$x_{n} = y_{n}$
for each
![]() $n \neq n_{0} \in \mathbb { N}$
. Using that
$n \neq n_{0} \in \mathbb { N}$
. Using that
![]() $g(x) = x_{n_{0}} f(x)$
also belongs to
$g(x) = x_{n_{0}} f(x)$
also belongs to
![]() $\mathcal {B}$
with
$\mathcal {B}$
with
![]() $\widehat {g}(S\setminus \{n_{0}\}) = \widehat {f}(S)$
if
$\widehat {g}(S\setminus \{n_{0}\}) = \widehat {f}(S)$
if
![]() $n_{0} \in S \subset _{fin} \mathbb { N}$
, we get:
$n_{0} \in S \subset _{fin} \mathbb { N}$
, we get:
 $$\begin{align*}\sum_{S}{|\widehat{f}(S) y_{S}|} = \sum_{n_{0} \notin S}{|\widehat{f}(S) x^{S}|} + |y_{n_{0}}|\, \sum_{n_{0} \in S}{|\widehat{f}(S) x_{S\setminus\{ n_{0}\}}|} < \infty. \end{align*}$$
$$\begin{align*}\sum_{S}{|\widehat{f}(S) y_{S}|} = \sum_{n_{0} \notin S}{|\widehat{f}(S) x^{S}|} + |y_{n_{0}}|\, \sum_{n_{0} \in S}{|\widehat{f}(S) x_{S\setminus\{ n_{0}\}}|} < \infty. \end{align*}$$
It is a simple observation that for every
![]() $f \in \mathcal {B}$
and for each permutation
$f \in \mathcal {B}$
and for each permutation
![]() $\sigma $
of the natural numbers, the function
$\sigma $
of the natural numbers, the function
![]() $f_{\sigma }$
defined by:
$f_{\sigma }$
defined by:
also belongs to
![]() $\mathcal {B}$
, which proves that condition
$\mathcal {B}$
, which proves that condition
![]() $\mathrm {(ii)}$
is sufficient. Finally, if
$\mathrm {(ii)}$
is sufficient. Finally, if
![]() $\mathrm {(iii)}$
is satisfied, then:
$\mathrm {(iii)}$
is satisfied, then:
Our aim is to find nice descriptions of
![]() $\operatorname {\mathrm {mon}}(V)$
for
$\operatorname {\mathrm {mon}}(V)$
for
![]() $V = \mathcal {B}$
,
$V = \mathcal {B}$
,
![]() $V = \mathcal {B}^{=m}$
and
$V = \mathcal {B}^{=m}$
and
![]() $V = \mathcal {B}^{\leq d}$
. It is clear that:
$V = \mathcal {B}^{\leq d}$
. It is clear that:
Using the Bohnenblust–Hille inequality from (6.5) (together with Hölder’s inequality and the multimonomial theorem) give that, for each
![]() $m\in \mathbb {N}$
, we have:
$m\in \mathbb {N}$
, we have:
Similar to Theorem 6.4.
![]() $\mathrm {(i)}$
, we even have the following full description.
$\mathrm {(i)}$
, we even have the following full description.
Theorem 6.9. For each positive integer m, one has:
Proof. We first prove that
![]() $\text {mon}(\mathcal {B}^{=m}) =\ell _{\frac {2m}{m-1}, \infty }$
. Given an m-homogeneous function
$\text {mon}(\mathcal {B}^{=m}) =\ell _{\frac {2m}{m-1}, \infty }$
. Given an m-homogeneous function
![]() $f\colon \{-1,1\}^{N} \rightarrow \mathbb { R}$
, we can find
$f\colon \{-1,1\}^{N} \rightarrow \mathbb { R}$
, we can find
![]() $F \in H^{m}_{\infty }(\mathbb {T}^\infty )$
with
$F \in H^{m}_{\infty }(\mathbb {T}^\infty )$
with
![]() $\widehat {F}(\alpha ) = \widehat {f}(\alpha )$
for all
$\widehat {F}(\alpha ) = \widehat {f}(\alpha )$
for all
![]() $\alpha \in \{ 0,1\}^{(\mathbb { N})}$
and
$\alpha \in \{ 0,1\}^{(\mathbb { N})}$
and
![]() $\widehat {F}(\alpha ) = 0$
, otherwise, and, such that:
$\widehat {F}(\alpha ) = 0$
, otherwise, and, such that:
where for this estimate, we use a result from [Reference Visser21] (see also the end of the proof of Theorem 6.5). This implies that
![]() $\operatorname {\mathrm {mon}}{H^{m}_{\infty }(\mathbb {T}^\infty )} \subset \operatorname {\mathrm {mon}} (\mathcal {B}^{=m})$
, which by Theorem 6.4.(i) gives the lower inclusion:
$\operatorname {\mathrm {mon}}{H^{m}_{\infty }(\mathbb {T}^\infty )} \subset \operatorname {\mathrm {mon}} (\mathcal {B}^{=m})$
, which by Theorem 6.4.(i) gives the lower inclusion:
Conversely, if
![]() $x \in \operatorname {\mathrm {mon}} (\mathcal {B}^{=m})$
, then by Proposition 6.8, also its decreasing rearrangement
$x \in \operatorname {\mathrm {mon}} (\mathcal {B}^{=m})$
, then by Proposition 6.8, also its decreasing rearrangement
![]() $r = (x_n^\ast ) \in \operatorname {\mathrm {mon}} (\mathcal {B}^{=m})$
. Thus, there is a constant
$r = (x_n^\ast ) \in \operatorname {\mathrm {mon}} (\mathcal {B}^{=m})$
. Thus, there is a constant
![]() $C> 0$
, such that, for each
$C> 0$
, such that, for each
![]() $f \in \mathcal {B}^{=m}$
, we get:
$f \in \mathcal {B}^{=m}$
, we get:
 $$\begin{align*}\sum_{|S| = m}{|\widehat{f}(S)|\,|r_{S}|} \leq C \, \| f\|_{\infty}. \end{align*}$$
$$\begin{align*}\sum_{|S| = m}{|\widehat{f}(S)|\,|r_{S}|} \leq C \, \| f\|_{\infty}. \end{align*}$$
We give a probabilistic argument and a Kislyakov type argument. The probabilistic argument: Let
![]() $A =\{S \subset [N], |S| = m\}$
. By the Kahane–Salem–Zygmund theorem (see (6.8) below), there is a choice of signs
$A =\{S \subset [N], |S| = m\}$
. By the Kahane–Salem–Zygmund theorem (see (6.8) below), there is a choice of signs
![]() $(\xi _{S})_{S \in A}$
, such that:
$(\xi _{S})_{S \in A}$
, such that:
 $$\begin{align*}\sum_{S \in A}{|\xi_{S}|r^{S}} \leq C \, \Big\| \sum_{S \in A}{\xi_{S} x^{S}} \Big\|_{\infty} \ll \, \sqrt{N} \sqrt{\binom{N}{m}}. \end{align*}$$
$$\begin{align*}\sum_{S \in A}{|\xi_{S}|r^{S}} \leq C \, \Big\| \sum_{S \in A}{\xi_{S} x^{S}} \Big\|_{\infty} \ll \, \sqrt{N} \sqrt{\binom{N}{m}}. \end{align*}$$
Since
![]() $(r_{n})_{n \in \mathbb { N}}$
is decreasing, we get:
$(r_{n})_{n \in \mathbb { N}}$
is decreasing, we get:
 $$\begin{align*}\binom{N}{m} \, r_{N}^{m} \ll \, \sqrt{N} \, \sqrt{\binom{N}{m}}, \end{align*}$$
$$\begin{align*}\binom{N}{m} \, r_{N}^{m} \ll \, \sqrt{N} \, \sqrt{\binom{N}{m}}, \end{align*}$$
and so for some constant
![]() $K_{m}$
independent of N, we have:
$K_{m}$
independent of N, we have:
 $$\begin{align*}r_{N}^m \leq C \sqrt{N} \binom{N}{m}^{-\frac{1}{2}} \ll_m \frac{\sqrt{N}}{N^{m/2}} . \end{align*}$$
$$\begin{align*}r_{N}^m \leq C \sqrt{N} \binom{N}{m}^{-\frac{1}{2}} \ll_m \frac{\sqrt{N}}{N^{m/2}} . \end{align*}$$
The Kislyakov argument: Consider the canonical embeddings:
where the first two embeddings are the canonical ones and the last comes from (2.2). The first one is isometric, the second one
![]() $2^{m-1}$
-isomorphic and the third
$2^{m-1}$
-isomorphic and the third
![]() $2$
-isomorphic. Then, we deduce from Theorem 3.2 that:
$2$
-isomorphic. Then, we deduce from Theorem 3.2 that:
 $$\begin{align*}r_N^{2m}\binom{N}{m} \leq \sum_{S \in A} |r^S|^2 \ll_m N. \end{align*}$$
$$\begin{align*}r_N^{2m}\binom{N}{m} \leq \sum_{S \in A} |r^S|^2 \ll_m N. \end{align*}$$
Since
![]() $\Big ( \frac {N}{m}\Big )^m \leq \binom {N}{m}$
, the argument completes. Finally, we prove that for each
$\Big ( \frac {N}{m}\Big )^m \leq \binom {N}{m}$
, the argument completes. Finally, we prove that for each
![]() $d \in \mathbb { N}$
, we have
$d \in \mathbb { N}$
, we have
![]() $\operatorname {\mathrm {mon}} (\mathcal {B}^{\leq d}) = \ell _{\frac {2d}{d-1}}$
. Using the fact that, for every
$\operatorname {\mathrm {mon}} (\mathcal {B}^{\leq d}) = \ell _{\frac {2d}{d-1}}$
. Using the fact that, for every
![]() $f \in \mathcal {B}^{\leq d}_N$
, we get by [Reference Klimek16],
$f \in \mathcal {B}^{\leq d}_N$
, we get by [Reference Klimek16],
where
![]() $f_m = \sum _{|S|=m} \widehat {f}(S) \chi _S$
denotes the m-homogeneous part of f, it easily follows that:
$f_m = \sum _{|S|=m} \widehat {f}(S) \chi _S$
denotes the m-homogeneous part of f, it easily follows that:
 $$\begin{align*}\ell_{\frac{2d}{d-1}, \infty} \subset \bigcap_{m=1}^{d}{\operatorname{\mathrm{mon}} (\mathcal{B}^{=m})} \subset \operatorname{\mathrm{mon}} (\mathcal{B}^{\leq d}) \subset \operatorname{\mathrm{mon}} (\mathcal{B}^{=d}) \subset \ell_{\frac{2d}{d-1}, \infty}. \\[-42pt] \end{align*}$$
$$\begin{align*}\ell_{\frac{2d}{d-1}, \infty} \subset \bigcap_{m=1}^{d}{\operatorname{\mathrm{mon}} (\mathcal{B}^{=m})} \subset \operatorname{\mathrm{mon}} (\mathcal{B}^{\leq d}) \subset \operatorname{\mathrm{mon}} (\mathcal{B}^{=d}) \subset \ell_{\frac{2d}{d-1}, \infty}. \\[-42pt] \end{align*}$$
Let us turn to the description of
![]() $\operatorname {\mathrm {mon}} (\mathcal {B})$
. We easily obtain:
$\operatorname {\mathrm {mon}} (\mathcal {B})$
. We easily obtain:
using the Cauchy–Schwarz inequality:
 $$\begin{align*}\sum_{S}{|\widehat{f}(S) x^{S}|} \leq \Big( \sum_{S}{|\widehat{f}(S)|^{2}} \Big)^{\frac{1}{2}} \Big( \sum_{S}{|x^{S}|^2} \Big)^{\frac{1}{2}} \leq \|f\|_{\infty} \Big(\prod_{n=1}^{\infty}{(1 + |x_{n}|^2)\Big)^{\frac{1}{2}}}. \end{align*}$$
$$\begin{align*}\sum_{S}{|\widehat{f}(S) x^{S}|} \leq \Big( \sum_{S}{|\widehat{f}(S)|^{2}} \Big)^{\frac{1}{2}} \Big( \sum_{S}{|x^{S}|^2} \Big)^{\frac{1}{2}} \leq \|f\|_{\infty} \Big(\prod_{n=1}^{\infty}{(1 + |x_{n}|^2)\Big)^{\frac{1}{2}}}. \end{align*}$$
Regarding the estimations from above, using the results for the m-homogeneous functions, we have:
This result can be improved.
Proposition 6.10. For every
![]() $ x \in \operatorname {\mathrm {mon}} (\mathcal {B})$
, one has:
$ x \in \operatorname {\mathrm {mon}} (\mathcal {B})$
, one has:
 $$ \begin{align*} \sup_{N \in \mathbb{ N}}{\, \frac{1}{\sqrt{N}} \sum_{n=1}^{N}{|x_{n}|}} < +\infty\, \end{align*} $$
$$ \begin{align*} \sup_{N \in \mathbb{ N}}{\, \frac{1}{\sqrt{N}} \sum_{n=1}^{N}{|x_{n}|}} < +\infty\, \end{align*} $$
and, in particular:
Proof. Using the majority function
![]() $\operatorname {\mathrm {Maj}}_{N}(x)$
(in fact, only its
$\operatorname {\mathrm {Maj}}_{N}(x)$
(in fact, only its
![]() $1$
-homogeneous part), we know from [Reference O’Donnell17] that for all S with
$1$
-homogeneous part), we know from [Reference O’Donnell17] that for all S with
![]() $|S|=1$
:
$|S|=1$
:
 $$\begin{align*}\widehat{\operatorname{\mathrm{Maj}}}_{N}(S) = \sqrt{\frac{2}{\pi}} \frac{1}{\sqrt{N}}. \end{align*}$$
$$\begin{align*}\widehat{\operatorname{\mathrm{Maj}}}_{N}(S) = \sqrt{\frac{2}{\pi}} \frac{1}{\sqrt{N}}. \end{align*}$$
Hence, for all
![]() $x \in \operatorname {\mathrm {mon}} (\mathcal {B})$
and every
$x \in \operatorname {\mathrm {mon}} (\mathcal {B})$
and every
![]() $N \in \mathbb {N}$
, we have:
$N \in \mathbb {N}$
, we have:
 $$\begin{align*}\sum_{n=1}^{N}{\sqrt{\frac{2}{\pi}} \frac{1}{\sqrt{N}} \, |x_{n}|} = \sum_{|S| = 1}{|\widehat{\operatorname{\mathrm{Maj}}}_{N}{(S)}| \, |x^{S}|} \leq \sum_{S \subset [N]}{|\widehat{\operatorname{\mathrm{Maj}}}_{N}{(S)}| \, |x^{S}|} \leq C_{x}, \end{align*}$$
$$\begin{align*}\sum_{n=1}^{N}{\sqrt{\frac{2}{\pi}} \frac{1}{\sqrt{N}} \, |x_{n}|} = \sum_{|S| = 1}{|\widehat{\operatorname{\mathrm{Maj}}}_{N}{(S)}| \, |x^{S}|} \leq \sum_{S \subset [N]}{|\widehat{\operatorname{\mathrm{Maj}}}_{N}{(S)}| \, |x^{S}|} \leq C_{x}, \end{align*}$$
the first estimate. Since the decreasing rearrangement
![]() $x^\ast $
by Proposition 6.8 also belongs to
$x^\ast $
by Proposition 6.8 also belongs to
![]() $\operatorname {\mathrm {mon}} (\mathcal {B})$
, the ‘in particular’ follows.
$\operatorname {\mathrm {mon}} (\mathcal {B})$
, the ‘in particular’ follows.
On the other hand, the use of the Kahane–Salem–Zygmund inequality (for Boolean functions, see, e.g. [Reference Defant, Mastyło and Pérez11, Lemma 3.1]) does not improve the condition from Proposition 6.10. Indeed, this inequality yields that for every
![]() $N \in \mathbb { N}$
and every family
$N \in \mathbb { N}$
and every family
![]() $(c_{S})_{S \subset [N]}$
in
$(c_{S})_{S \subset [N]}$
in
![]() $\mathbb {R}$
, there is a choice of signs
$\mathbb {R}$
, there is a choice of signs
![]() $(\xi _{S})_{S \subset [N]}$
, such that:
$(\xi _{S})_{S \subset [N]}$
, such that:
 $$ \begin{align} \sum_{S \subset [N]}{|c_{S}| |x^{S}|} \leq C_{x} \, \Big\| \sum_{S \subset [N]}{\xi_{S} c_{S} x^{S}} \Big\|_{\infty} \leq C_{x} \, 6 \sqrt{\log{2}} \, \sqrt{N}\, \Big( \sum_{S \subset [N]}{|c_{S}|^{2}} \Big)^{1/2}. \end{align} $$
$$ \begin{align} \sum_{S \subset [N]}{|c_{S}| |x^{S}|} \leq C_{x} \, \Big\| \sum_{S \subset [N]}{\xi_{S} c_{S} x^{S}} \Big\|_{\infty} \leq C_{x} \, 6 \sqrt{\log{2}} \, \sqrt{N}\, \Big( \sum_{S \subset [N]}{|c_{S}|^{2}} \Big)^{1/2}. \end{align} $$
Taking the supremum over all
![]() $(c_{S})_{S \subset [N]}$
with
$(c_{S})_{S \subset [N]}$
with
![]() $\ell _{2}$
-norm equal to one, we deduce that:
$\ell _{2}$
-norm equal to one, we deduce that:
 $$ \begin{align} \prod_{n=1}^{N}{(1 + x_{n}^{2})} = \Big(\sum_{S \subset [N]}{|x^{S}|^{2}}\Big)^{1/2} \leq C_{x} \, 6 \sqrt{\log{2}} \, \sqrt{N}. \end{align} $$
$$ \begin{align} \prod_{n=1}^{N}{(1 + x_{n}^{2})} = \Big(\sum_{S \subset [N]}{|x^{S}|^{2}}\Big)^{1/2} \leq C_{x} \, 6 \sqrt{\log{2}} \, \sqrt{N}. \end{align} $$
Since
![]() $(x_{n})_{n \in \mathbb { N}}$
converges to zero, we can find a positive constant
$(x_{n})_{n \in \mathbb { N}}$
converges to zero, we can find a positive constant
![]() $\alpha> 0$
, such that
$\alpha> 0$
, such that
![]() $\exp {(\alpha |x_{n}|^{2})} \leq 1 + |x_{n}|^{2}$
for every
$\exp {(\alpha |x_{n}|^{2})} \leq 1 + |x_{n}|^{2}$
for every
![]() $n \in \mathbb { N}$
, so that:
$n \in \mathbb { N}$
, so that:
 $$\begin{align*}\exp{( \alpha \sum_{n=1}^{N}{|x_{n}|^{2}} )} \leq \prod_{n=1}^{N}{(1 + x_{n}^{2})} \leq C_{x} \, 6 \sqrt{\log{2}} \, \sqrt{N}. \end{align*}$$
$$\begin{align*}\exp{( \alpha \sum_{n=1}^{N}{|x_{n}|^{2}} )} \leq \prod_{n=1}^{N}{(1 + x_{n}^{2})} \leq C_{x} \, 6 \sqrt{\log{2}} \, \sqrt{N}. \end{align*}$$
It follows that:
 $$ \begin{align} \sup_{N \in \mathbb{ N}}{ \, \frac{1}{\log{N}}\sum_{n=1}^{N}{|x_{n}|^{2}}} < +\infty. \end{align} $$
$$ \begin{align} \sup_{N \in \mathbb{ N}}{ \, \frac{1}{\log{N}}\sum_{n=1}^{N}{|x_{n}|^{2}}} < +\infty. \end{align} $$
But this condition is weaker than what we got in Proposition 6.10, since:
 $$\begin{align*}\frac{1}{\log{N}} \sum_{n=1}^{N}{|x_{n}|^{2}} \leq \frac{1}{\log{N}} \sum_{n=1}^{N}{|x_{n}^\ast|^{2}} \leq \frac{\| x\|_{\ell_{2, \infty}}^{2}}{\log{N}} \sum_{n=1}^{N}{\frac{1}{n}} \leq \| x\|_{\ell_{2, \infty}}^{2}. \end{align*}$$
$$\begin{align*}\frac{1}{\log{N}} \sum_{n=1}^{N}{|x_{n}|^{2}} \leq \frac{1}{\log{N}} \sum_{n=1}^{N}{|x_{n}^\ast|^{2}} \leq \frac{\| x\|_{\ell_{2, \infty}}^{2}}{\log{N}} \sum_{n=1}^{N}{\frac{1}{n}} \leq \| x\|_{\ell_{2, \infty}}^{2}. \end{align*}$$
Finally, we establish the following analog of statement
![]() $(2)$
from Theorem 6.4.
$(2)$
from Theorem 6.4.
Proposition 6.11. For each
![]() $x \in \operatorname {\mathrm {mon}} (\mathcal {B})$
, one has:
$x \in \operatorname {\mathrm {mon}} (\mathcal {B})$
, one has:
 $$\begin{align*}\limsup_{N \to \infty} \frac{1}{\log N} \sum_{n=1}^N (x^\ast_n)^2 \leq 1. \end{align*}$$
$$\begin{align*}\limsup_{N \to \infty} \frac{1}{\log N} \sum_{n=1}^N (x^\ast_n)^2 \leq 1. \end{align*}$$
Proof. We write
![]() $r=(r_{n})_{n \in \mathbb { N}}$
for the decreasing rearrangement of
$r=(r_{n})_{n \in \mathbb { N}}$
for the decreasing rearrangement of
![]() $(|x_{n}|)_{n \in \mathbb { N}}$
. Then:
$(|x_{n}|)_{n \in \mathbb { N}}$
. Then:
and, hence, by Theorem 6.5.
![]() $(i)$
, we have that there is a constant
$(i)$
, we have that there is a constant
![]() $C = C(r)$
, such that for all N:
$C = C(r)$
, such that for all N:
 $$\begin{align*}\sum_{ S \subset [N]}{r_{S}^{2}} \leq C \, N; \end{align*}$$
$$\begin{align*}\sum_{ S \subset [N]}{r_{S}^{2}} \leq C \, N; \end{align*}$$
again, there is an alternative proof using the Kahane–Salem–Zygmund inequality (in the form of (6.8) and (6.9)). We claim that:
 $$\begin{align*}\frac{(r_{m}^{2} + \ldots + r_{N}^{2})^{m}}{m!} \leq \sum_{|S| = m}{r_{S}^{2}}. \end{align*}$$
$$\begin{align*}\frac{(r_{m}^{2} + \ldots + r_{N}^{2})^{m}}{m!} \leq \sum_{|S| = m}{r_{S}^{2}}. \end{align*}$$
We postpone the proof of the claim to end. The claim yields by Stirling’s inequality that there is a positive constant
![]() $C'$
depending just on r, such that:
$C'$
depending just on r, such that:
Putting
![]() $m=\log {N}$
, we arrive to the inequality:
$m=\log {N}$
, we arrive to the inequality:
 $$\begin{align*}\limsup_{N}{\frac{r_{\log{N}}^{2} + \ldots + r_{N}^{2}}{\log{N}}} \leq 1. \end{align*}$$
$$\begin{align*}\limsup_{N}{\frac{r_{\log{N}}^{2} + \ldots + r_{N}^{2}}{\log{N}}} \leq 1. \end{align*}$$
Since
![]() $r_{n}^{2}$
converges to zero, we immediately conclude that:
$r_{n}^{2}$
converges to zero, we immediately conclude that:
 $$\begin{align*}\limsup_{N}{\frac{r_{1}^{2} + \ldots + r_{N}^{2}}{\log{N}}} \leq 1. \end{align*}$$
$$\begin{align*}\limsup_{N}{\frac{r_{1}^{2} + \ldots + r_{N}^{2}}{\log{N}}} \leq 1. \end{align*}$$
To prove the claim, note that every
![]() $S \subset \mathbb { N}$
with
$S \subset \mathbb { N}$
with
![]() $|S| = m$
is determined by the subset
$|S| = m$
is determined by the subset
![]() $S_{1}$
of elements n with
$S_{1}$
of elements n with
![]() $n < m$
and the subset
$n < m$
and the subset
![]() $S_{2}$
of those with
$S_{2}$
of those with
![]() $n \geq m$
. Then, we can find unique finite sequences
$n \geq m$
. Then, we can find unique finite sequences
![]() $m \leq i_{1}, i_{2}, \ldots , i_{k} \leq N$
and
$m \leq i_{1}, i_{2}, \ldots , i_{k} \leq N$
and
![]() $m_{1}, m_{2}, \ldots , m_{k}$
in
$m_{1}, m_{2}, \ldots , m_{k}$
in
![]() $\mathbb { N}$
with
$\mathbb { N}$
with
![]() $m_{1}+ \ldots + m_{k}=m$
and, such that:
$m_{1}+ \ldots + m_{k}=m$
and, such that:
 $$ \begin{align*} S^{c} \cap \{n \colon \, n < m \} & = \{m_{1}, m_{1} + m_{2}, \ldots, m_{1} + \ldots + m_{k-1}\}\\ S \cap \{n\colon \, n \geq m \} & = \{i_{1} < i_{2} < \ldots < i_{k}\}. \end{align*} $$
$$ \begin{align*} S^{c} \cap \{n \colon \, n < m \} & = \{m_{1}, m_{1} + m_{2}, \ldots, m_{1} + \ldots + m_{k-1}\}\\ S \cap \{n\colon \, n \geq m \} & = \{i_{1} < i_{2} < \ldots < i_{k}\}. \end{align*} $$
We can then rewrite
![]() $r_{S}$
as:
$r_{S}$
as:
and using that
![]() $(r_{n})_{n \in \mathbb { N}}$
is nonincreasing, we deduce that:
$(r_{n})_{n \in \mathbb { N}}$
is nonincreasing, we deduce that:
Therefore:
 $$ \begin{align*} m! \sum_{|S| = m}{r_{S}^{2}} & \geq \sum_{\substack{ (\alpha_{m}, \ldots, \alpha_{N}) \in \mathbb{N}_{0}^{N-m+1} |\alpha| = m}}{\binom{m}{\alpha} r_{m}^{\alpha_{m}} \cdot r_{m+1}^{\alpha_{m+1}}\cdot \ldots \cdot r_{N}^{\alpha_{N}} } \\ & = (r_{m} + \ldots + r_{N})^{m} , \end{align*} $$
$$ \begin{align*} m! \sum_{|S| = m}{r_{S}^{2}} & \geq \sum_{\substack{ (\alpha_{m}, \ldots, \alpha_{N}) \in \mathbb{N}_{0}^{N-m+1} |\alpha| = m}}{\binom{m}{\alpha} r_{m}^{\alpha_{m}} \cdot r_{m+1}^{\alpha_{m+1}}\cdot \ldots \cdot r_{N}^{\alpha_{N}} } \\ & = (r_{m} + \ldots + r_{N})^{m} , \end{align*} $$
and the proof completes.
Acknowledgments
The second named author was supported by the National Science Centre, Poland, Grant no. 2019/33/B/ST1/00165. The third named author acknowledges support from the grants ‘Juan de la Cierva Formación’ (FJC2018-036519-I) and 2021-MAT11 (ETSI Industriales, UNED).
Competing Interests
The author(s) declare none.