Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-06-12T12:59:11.966Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Li-type criterion for zero-free regions of certain Dirichlet series with real coefficients

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  01 October 2016

Alina Bucur ,
Anne-Maria Ernvall-Hytönen ,
Almasa Odžak  and
Lejla Smajlović
Alina Bucur
Affiliation:
Department of Mathematics, University of California at San Diego, 9500 Gilman Dr #0112, La Jolla, CA 92093, USA email alina@math.ucsd.edu
Anne-Maria Ernvall-Hytönen
Affiliation:
Department of Mathematics and Statistics, Åbo Akademi University, Fänriksgatan 3, 20500 Åbo, Finland email anne-maria.ernvall-hytonen@abo.fi
Almasa Odžak
Affiliation:
Department of Mathematics, University of Sarajevo, Zmaja od Bosne 35, 71000 Sarajevo, Bosnia and Herzegovina email almasa.odzak@pmf.unsa.ba
Lejla Smajlović
Affiliation:
Department of Mathematics, University of Sarajevo, Zmaja od Bosne 35, 71000 Sarajevo, Bosnia and Herzegovina email lejlas@pmf.unsa.ba

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Li coefficients 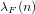$\unicode[STIX]{x1D706}_{F}(n)$ of a zeta or $L$-function 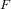$F$ provide an equivalent criterion for the (generalized) Riemann hypothesis. In this paper we define these coefficients, and their generalizations, the $\unicode[STIX]{x1D70F}$-Li coefficients, for a subclass of the extended Selberg class which is known to contain functions violating the Riemann hypothesis such as the Davenport–Heilbronn zeta function. The behavior of the $\unicode[STIX]{x1D70F}$-Li coefficients varies depending on whether the function in question has any zeros in the half-plane 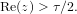$\text{Re}(z)>\unicode[STIX]{x1D70F}/2.$ We investigate analytically and numerically the behavior of these coefficients for such functions in both the $n$ and $\unicode[STIX]{x1D70F}$ aspects.

MSC classification

Primary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses 11M36: Selberg zeta functions and regularized determinants; applications to spectral theory, Dirichlet series, Eisenstein series, etc. Explicit formulas
Secondary: 11M41: Other Dirichlet series and zeta functions
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Issue 1 , 2016 , pp. 259 - 280
Copyright
© The Author(s) 2016 

References

Balanzario, E. P. and Sánchez-Ortiz, J., ‘Zeros of the Davenport–Heilbronn counterexample’, Math. Comp. 76 (2007) 2045–2049.Google Scholar
Bombieri, E. and Ghosh, A., ‘Around Davenport–Heilbronn function’, Uspekhi Mat. Nauk 66 (2011) 15–66 (Russian); Russian Math. Surveys 66 (2011) 221–270 (English).Google Scholar
Bombieri, E. and Lagarias, J. C., ‘Complements to Li’s criterion for the Riemann hypothesis’, J. Number Theory 77 (1999) 274–287.Google Scholar
Bucur, A., Ernvall-Hytönen, A.-M., Odžak, A., Roditty-Gershon, E. and Smajlović, L., ‘On 𝜏-Li coefficients for Rankin–Selberg L-functions’, Women in numbers Europe , Association for Women in Mathematics Series 2 (ed. Bucur, A. et al. ; Springer International, Switzerland, 2015) 167–190.CrossRefGoogle Scholar
Davenport, H. and Heilbronn, H., ‘On the zeros of certain Dirichlet series (second paper)’, J. Lond. Math. Soc. (2) 11 (1936) 307–312.Google Scholar
Droll, A. D., ‘Variations of Li’s criterion for an extension of the Selberg class’, PhD Thesis, Queen’s University Ontario, Canada, 2012; available at http://qspace.library.queensu.ca/jspui/bitstream/1974/7352/1/Droll_Andrew_D_201207_PhD.pdf.Google Scholar
Ernvall-Hytönen, A.-M., Odžak, A., Smajlović, L. and Sušić, M., ‘On the modified Li criterion for a certain class of L-functions’, J. Number Theory 156 (2015) 340–367.Google Scholar
Johansson, F., ‘Arb: a C library for ball arithmetic’, ACM Commun. Comput. Algebra 47 (2013) no. 4, 166–169.CrossRefGoogle Scholar
Kaczorowski, J., ‘Axiomatic theory of L functions: the Selberg class’, Analytic number theory, C.I.M.E. Summer School, Cetraro, Italy, 2002 , Lecture Notes in Mathematics 1891 (eds Perelli, A. and Viola, C.; Springer, 2006) 133–209.Google Scholar
Kaczorowski, J. and Perelli, A., ‘On the structure of the Selberg class, I: 0⩽d⩽1’, Acta Math. 182 (1999) 207–241.Google Scholar
Lagarias, J. C., ‘Li coefficients for automorphic L-functions’, Ann. Inst. Fourier 57 (2007) 1689–1740.Google Scholar
Maslanka, K., ‘Li’s criterion for the Riemann hypothesis — numerical approach’, Opuscula Math. 24 (2004) no. 1, 103–114.Google Scholar
Mazhouda, K., ‘On the 𝜏-Li coefficients for automorphic L-functions’, Rocky Mountain J. Math., to appear.Google Scholar
Omar, S., Ouni, R. and Mazhouda, K., ‘On the zeros of Dirichlet L-functions’, LMS J. Comput. Math. 14 (2011) 140–154.Google Scholar
Proskurin, N. V., ‘On the cubic L-function’, St. Petersburg Math. J. 24 (2013) no. 2, 353–370.CrossRefGoogle Scholar
Selberg, A., ‘Old and new conjectures and results about a class of Dirichlet series’, Proceedings of Amalfi Conference on Analytic Number Theory (ed. Bombieri, E. et al. ; Università di Salerno, 1992) 367–385.Google Scholar
Smajlović, L., ‘On Li’s criterion for the Riemann hypothesis for the Selberg class’, J. Number Theory 130 (2010) 828–851.Google Scholar
Titchmarsh, E. C., The theory of the Riemann zeta-function (Clarendon Press, Oxford, 1951).Google Scholar