Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-06-08T14:44:10.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of generalised exponential maps

Part of: Complex dynamical systems Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  21 April 2022

PATRICK COMDÜHR ,
VASILIKI EVDORIDOU  and
DAVID J. SIXSMITH
PATRICK COMDÜHR
Affiliation:
Mathematisches Seminar, Christian-Albrechts-Universität zu Kiel, Ludewig-Meyn-Str. 4, D-24098 Kiel, Germany e-mail: comduehr@math.uni-kiel.de
VASILIKI EVDORIDOU
Affiliation:
School of Mathematics and Statistics, The Open University, Milton Keynes MK7 6AA e-mails: vasiliki.evdoridou@open.ac.uk, david.sixsmith@open.ac.uk
DAVID J. SIXSMITH
Affiliation:
School of Mathematics and Statistics, The Open University, Milton Keynes MK7 6AA e-mails: vasiliki.evdoridou@open.ac.uk, david.sixsmith@open.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Since 1984, many authors have studied the dynamics of maps of the form 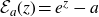$\mathcal{E}_a(z) = e^z - a$ , with 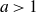$a > 1$ . It is now well-known that the Julia set of such a map has an intricate topological structure known as a Cantor bouquet, and much is known about the dynamical properties of these functions.

It is rather surprising that many of the interesting dynamical properties of the maps 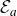$\mathcal{E}_a$ actually arise from their elementary function theoretic structure, rather than as a result of analyticity. We show this by studying a large class of continuous 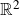$\mathbb{R}^2$ maps, which, in general, are not even quasiregular, but are somehow analogous to 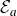$\mathcal{E}_a$ . We define analogues of the Fatou and the Julia set and we prove that this class has very similar dynamical properties to those of 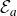$\mathcal{E}_a$ , including the Cantor bouquet structure, which is closely related to several topological properties of the endpoints of the Julia set.

MSC classification

Primary: 37F10: Polynomials; rational maps; entire and meromorphic functions
Secondary: 30D05: Functional equations in the complex domain, iteration and composition of analytic functions
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 1 , January 2023 , pp. 123 - 136
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by Engineering and Physical Sciences Research Council grant EP/R010560/1.

References

Aarts, Jan M. and Oversteegen, Lex G. The geometry of Julia sets. Trans. Amer. Math. Soc. 338(2) (1993), 897–918.CrossRefGoogle Scholar
Alhabib, Nada and Rempe-Gillen, Lasse Escaping endpoints Explode. Comput. Methods Funct. Theory, 17(1) (2017), 65–100.CrossRefGoogle Scholar
Bergweiler, Walter Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29(2) (1993), 151–188.CrossRefGoogle Scholar
Bergweiler, Walter Karpińska’s paradox in dimension 3. Duke Math. J. 154(3) (2010), 599–630.CrossRefGoogle Scholar
Barański, Krzysztof, Jarque, Xavier, and Rempe, Lasse Brushing the hairs of transcendental entire functions. Topology Appl., 159(8) (2012), 2102–2114.CrossRefGoogle Scholar
Bergweiler, Walter and Nicks, Daniel A. Foundations for an iteration theory of entire quasiregular maps. Israel J. Math., 201(1) (2014), 147–184.CrossRefGoogle Scholar
Devaney, Robert L. and Krych, Michał Dynamics of ${\rm exp}(z)$ . Ergodic Theory Dynam. Systems, 4(1) (1984), 35–52.CrossRefGoogle Scholar
Devaney, Robert L. and Tangerman, Folkert Dynamics of entire functions near the essential singularity. Ergodic Theory Dynam. Systems, 6(4) (1986), 489–503.CrossRefGoogle Scholar
Karpińska, Bogusława Hausdorff dimension of the hairs without endpoints for $\lambda\exp z$ . C. R. Acad. Sci. Paris Sér. I Math., 328(11) (1999), 1039–1044.CrossRefGoogle Scholar
Mayer, John C. An explosion point for the set of endpoints of the Julia set of $\lambda\exp(z)$ . Ergodic Theory Dynam. Systems, 10(1) (1990), 177–183.CrossRefGoogle Scholar
Nadler, Sam B., Jr. Continuum theory, Monographs and Textbooks in Pure and Applied Mathematics Vol. 158 (Marcel Dekker, Inc., New York, 1992).Google Scholar
Rempe, Lasse Topological dynamics of exponential maps on their escaping sets. Ergodic Theory Dynam. Systems, 26(6) (2006), 1939–1975.CrossRefGoogle Scholar
Günter Rottenfusser, Johannes Rückert, Rempe, Lasse and Schleicher, Dierk Dynamic rays of bounded-type entire functions. Ann. of Math. (2), 173(1), (2011) 77–125.CrossRefGoogle Scholar
Lasse Rempe, Philip J. Rippon, and Gwyneth M. Stallard. Are Devaney hairs fast escaping? J. Difference Equ. Appl., 16(5-6) (2010), 739–762.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M. Slow escaping points of meromorphic functions. Trans. Amer. Math. Soc., 363(8) (2011), 4171–4201.CrossRefGoogle Scholar
Schleicher, Dierk Dynamics of entire functions. In Holomorphic Dynamical Systems Lecture Notes in Math. vol. 1998 (Springer, Berlin, (2010 p. 295–339.).CrossRefGoogle Scholar