Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-31T16:46:15.862Z Has data issue: false hasContentIssue false
  • English
  • Français

Variation of the algebraic λ-invariant over a solvable extension

Part of: Algebraic number theory: global fields Arithmetic algebraic geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  21 November 2019

DANIEL DELBOURGO
DANIEL DELBOURGO*
Affiliation:
Department of Mathematics and Statistics The University of Waikato, 3rd Floor, G. Block, Gate 8, Hillcrest Road, Hamilton, New Zealand 3240 e-mail: daniel.delbourgo@waikato.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Fix an odd prime p. Let 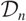$\mathcal{D}_n$ denote a non-abelian extension of a number field K such that 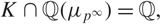$K\cap\mathbb{Q}(\mu_{p^{\infty}})=\mathbb{Q}, $ and whose Galois group has the form 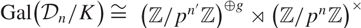$ \text{Gal}\big(\mathcal{D}_n/K\big)\cong \big(\mathbb{Z}/p^{n'}\mathbb{Z}\big)^{\oplus g}\rtimes \big(\mathbb{Z}/p^n\mathbb{Z}\big)^{\times}\ $ where g > 0 and 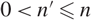$0 \lt n'\leq n$. Given a modular Galois representation 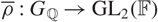$\overline{\rho}:G_{\mathbb{Q}}\rightarrow \text{GL}_2(\mathbb{F})$ which is p-ordinary and also p-distinguished, we shall write 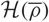$\mathcal{H}(\overline{\rho})$ for the associated Hida family. Using Greenberg’s notion of Selmer atoms, we prove an exact formula for the algebraic λ-invariant

\begin{equation}\lambda^{\text{alg}}_{\mathcal{D}_n}(f) \;=\; \text{the number of zeroes of }\text{char}_{\Lambda}\big(\text{Sel}_{\mathcal{D}_n^{\text{cy}}}\big(f\big)^{\wedge}\big)\end{equation}
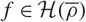at all $f\in\mathcal{H}(\overline{\rho})$, under the assumption 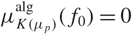$\mu^{\text{alg}}_{K(\mu_p)}(f_0)=0$ for at least one form f0. We can then easily deduce that 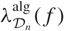$\lambda^{\text{alg}}_{\mathcal{D}_n}(f)$ is constant along branches of 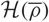$\mathcal{H}(\overline{\rho})$, generalising a theorem of Emerton, Pollack and Weston for 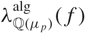$\lambda^{\text{alg}}_{\mathbb{Q}(\mu_{p})}(f)$.

For example, if $\mathcal{D}_{\infty}=\bigcup_{n\geq 1}\mathcal{D}_n$ has the structure of a p-adic Lie extension then our formulae include the cases where: either (i) 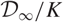$\mathcal{D}_{\infty}/K$ is a g-fold false Tate tower, or (ii) 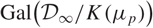$\text{Gal}\big(\mathcal{D}_{\infty}/K(\mu_p)\big)$ has dimension ≤ 3 and is a pro-p-group.

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms
Secondary: 11F80: Galois representations 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture 11R23: Iwasawa theory

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 170 , Issue 3 , May 2021 , pp. 499 - 521
Copyright
© Cambridge Philosophical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Bertolini, M. and Darmon, H. Iwasawa’s main conjecture for elliptic curves over anticyclotomic $\mathbb{Z}_p$-extensions. Annals of Mathematics 162 (2005), 1–64.CrossRefGoogle Scholar
Castella, F., Kim, C.-H. and Longo, M.. Variation of anticyclotomic Iwasawa invariants in Hida families. Algebra Number Theory 11 (2017), 2339–2368.CrossRefGoogle Scholar
Chida, M. and Hsieh, M.-L.. On the anticyclotomic main conjecture for modular forms. Compositio Math. 151 (2015), 863–897.CrossRefGoogle Scholar
Coates, J. and Sujatha, R.. Fine Selmer groups of elliptic curves over p-adic Lie extensions. Math. Ann. 331 (2005), 809–839.Google Scholar
Darmon, H. and Tian, Y.. Heegner points over towers of Kummer extensions. Canadian J. Math. 62 (2010), 1060–1082.CrossRefGoogle Scholar
Delbourgo, D.. Variation of the analytic λ-invariant over a solvable extension, to appear in the Proc London Math Soc.Google Scholar
Delbourgo, D. and Lei, A.. Estimating the growth in Mordell–Weil ranks and Shafarevich-Tate groups over Lie extensions. Ramanujan Journal 43 (2017), 29–68.CrossRefGoogle Scholar
Delbourgo, D. and Peters, L.. Higher order congruences amongst Hasse–Weil L-values. J. Aust. Math. Society 98 (2015), 1–38.CrossRefGoogle Scholar
Delbourgo, D. and Qin, C.. K1-congruences for three-dimensional Lie groups. Annales Math. du Québec 43 (2019), 161–211.CrossRefGoogle Scholar
Deligne, P.. Formes modulaires et représentations l-adiques, Séminaires Bourbaki. Lecture Notes in Math. 179 (Springer Verlag 1969), 139–172.CrossRefGoogle Scholar
Emerton, M., Pollack, R. and Weston, T.. Variation of Iwasawa invariants in Hida families. Inventi. Math. 163 (2006), 523–580.CrossRefGoogle Scholar
Greenberg., R. Iwasawa theory for elliptic curves, in Arithmetic Theory of Elliptic Curves, Cetraro (1997), Lecture Notes in Math. 1716 (1997), 51–144.CrossRefGoogle Scholar
Greenberg, R.. Iwasawa theory, projective modules, and modular representations. Mem. Ameri. Math. Soc. 992 (2011), 185 pages.Google Scholar
Greenberg, R. and Vatsal, V.. On the Iwasawa invariants of elliptic curves. Inventi. Math. 142 (2000), 17–63.CrossRefGoogle Scholar
Hida, H.. Galois representations into $\text{GL}_2(\mathbb{Z}_p[[X]])$. Inventi. Math. 85 (1986), 545–613.CrossRefGoogle Scholar
Jha, S.. Fine Selmer group of Hida deformations over non-commutative p-adic Lie extensions. Asian Journal Math. 16 (2012), 353–366.CrossRefGoogle Scholar
Kato, K.. p-adic Hodge theory and values of zeta functions of modular forms. Astérisque 295 ix (2004), 117-290.Google Scholar
Khare, C. and Wintenberger, J.-P.. Serre’s modularity conjecture I. Inventi. Math. 178 (2009), 485–504.CrossRefGoogle Scholar
Lim, M. F.. $\mathfrak{M}_H(G)$-property and congruence of Galois representations. preprint 2019.Google Scholar
Livné, R.. On the conductors of mod l Galois representations coming from modular forms. J. Number Theory 31 (1989), 133–141.CrossRefGoogle Scholar
Mazur, B., Tate, J. and Teitelbaum, J.. On p-adic analogues of the conjectures of Birch and Swinnerton-Dyer. Inventi. Math. 84 (1986), 1–48.CrossRefGoogle Scholar
Pollack, R. and Weston, T.. On anticyclotomic μ-invariants of modular forms. Compositio Math. 147 (2011), 1353–1381.CrossRefGoogle Scholar
Serre, J.-P.. Linear representations of finite groups. Graduate Texts in Math. 42, (Springer–Verlag, New York 1977).CrossRefGoogle Scholar
Shekar, S. and Sujatha, R.. On the structure of Selmer groups of Λ-adic deformations over p-adic Lie extensions. Documenta Math. 17 (2012), 573–606.Google Scholar