Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-05-19T05:10:34.025Z Has data issue: false hasContentIssue false
  • English
  • Français

Additive Diophantine inequalities with mixed powers I

Published online by Cambridge University Press:  26 February 2010

Jörg Brüdern
Jörg Brüdern
Affiliation:
Geismar Landstrasse 97, 3400 Göttingen, West Germany.
Get access

Extract

In this paper we shall be concerned with the following problem. Let k1 ≤ k2 ≤…≤ ks be natural numbers, λ1,…, λs be nonzero real numbers, not all of the same sign. Is it then true that the values taken by

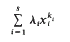
at integer points (x1,…, xs) ∈ ℤk are dense on the real line, provided at least one of the ratios λi/λj, is irrational? We shall refer to this, for brevity, as the inequality problem for k1,…, ks. Optimistically one may conjecture that the inequality problem is true whenever

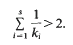
Type
Research Article
Information
Mathematika , Volume 34 , Issue 2 , December 1987 , pp. 124 - 130
Copyright
Copyright © University College London 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baker, R. C. and Harman, G.. Diophantine inequalities with mixed powers. J. Number Theory, 18 (1984), 69–85.CrossRefGoogle Scholar
2.Cook, R. J.. Diophantine inequalities with mixed powers. J. Number Theory, 9 (1977), 261–274.CrossRefGoogle Scholar
3.Cook, R. J.. Diophantine inequalities with mixed powers II. J. Number Theory, 11 (1979), 49–68.CrossRefGoogle Scholar
4.Davenport, H.. Indefinite quadratic forms in many variables. Mathematika, 3 (1956), 81–101.CrossRefGoogle Scholar
5.Davenport, H. and Heilbronn, H.. On indefinite quadratic forms in five variables. J. Lond. Math. Soc., 21 (1946), 185–193.CrossRefGoogle Scholar
6.Davenport, H. and Roth, K. F.. The solubility of certain Diophantine inequalities. Mathematika, 2 (1955), 81–96.CrossRefGoogle Scholar
7.Tsang, K. M.. Diophantine inequalities with mixed powers. J. Number Theory, 15 (1982) 149–163.CrossRefGoogle Scholar
8.Vaughan, R. C.. Diophantine approximation by prime numbers II, Proc. Lond. Math. Soc., (3), 28 (1974), 385–401.CrossRefGoogle Scholar
9.Vaughan, R. C.. The Hardy-Littlewood method (Cambridge, 1981).Google Scholar