Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-19T05:35:32.641Z Has data issue: false hasContentIssue false
  • English
  • Français

The depth of the semigroup of balanced endomorphisms

Part of: Semigroups

Published online by Cambridge University Press:  26 February 2010

John B. Fountain
John B. Fountain
Affiliation:
Department of Mathematics, University of York, Heslington, York. YOI 5DD.
Get access

Extract

Let X be an infinite set and T(X) be the full transformation semigroup on X. In [4] and [6] Howie gives a description of the subsemigroup of T(X) generated by its idempotents. In order to do this he defines, for α in T(X),

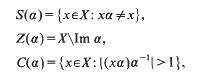
and refers to the cardinals s(α) = |S(α)|, d(α) = |Z(α)| and |c(α) = |C(α)| as the shift, the defect, and the collapse of α respectively. Then putting

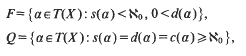
he proves that the subsemigroup of T(X) generated by its idempotents is 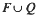. Furthermore, both F and Q are generated by their idempotents

MSC classification

Secondary: 20M20: Semigroups of transformations, etc.
Type
Research Article
Information
Mathematika , Volume 41 , Issue 1 , June 1994 , pp. 199 - 208
Copyright
Copyright © University College London 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Fountain, J. B. and Lewin, A. M.. Products of idempotent endomorphisms of an independence algebra of infinite rank. Math. Proc. Camb. Phil. Soc., 114 (1993), 303–319.CrossRefGoogle Scholar
2.Gould, V. A. R..Endomorphism monoids of independence algebras. To appear in Algebra Universalis.Google Scholar
3.Grätzer, G. Universal Algebra. Van Nostrand, Princeton, (1968).Google Scholar
4.Howie, J. M. The subsemigroup generated by the idempotents of a full transformation semigroup. J. London Math. Soc., 41 (1966), 707–716.CrossRefGoogle Scholar
5.Howie, J. M. An Introduction to Semigroup Theory. Academic Press, London, (1976).Google Scholar
6.Howie, J. M.. Some subsemigroups of infinite full transformation semigroups. Proc. Roy. Soc. Edinburgh Sect. A, 88 (1981), 159–167.CrossRefGoogle Scholar
7.Jones, P. R.. Exchange properties and basis properties for closure operators. Colloq. Math., 37 (1989), 29–33.CrossRefGoogle Scholar
8.McKenzie, R. N., McNulty, G. F. and Taylor, W. F.. Algebra, Lattices, Varieties, Vol. I (Wadsworth, Monterey, (1983).Google Scholar
9.Narkiewicz, W.. Independence in a certain class of abstract algebras. Fund. Math., 50 (1961/1962), 333–340.CrossRefGoogle Scholar
10.Reynolds, M. A. and Sullivan, R. P.. Products of idempotent linear transformations. Proc. Royal Soc. Edinburgh Sect. A, 100 (1985), 123–138.CrossRefGoogle Scholar