Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-05-19T12:14:47.426Z Has data issue: false hasContentIssue false
  • English
  • Français

DIVISOR-SUM FIBERS

Part of: Multiplicative number theory

Published online by Cambridge University Press:  03 April 2018

Paul Pollack ,
Carl Pomerance  and
Lola Thompson
Paul Pollack
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA 30602, U.S.A. email pollack@uga.edu
Carl Pomerance
Affiliation:
Department of Mathematics, Dartmouth College, Hanover, NH 03755, U.S.A. email carlp@math.dartmouth.edu
Lola Thompson
Affiliation:
Department of Mathematics, Oberlin College, Oberlin, OH 44074, U.S.A. email lola.thompson@oberlin.edu
Get access

Abstract

Let 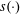$s(\cdot )$ denote the sum-of-proper-divisors function, that is, 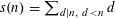$s(n)=\sum _{d\mid n,~d<n}d$. Erdős, Granville, Pomerance, and Spiro conjectured that for any set 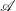$\mathscr{A}$ of asymptotic density zero, the preimage set 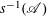$s^{-1}(\mathscr{A})$ also has density zero. We prove a weak form of this conjecture: if 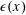$\unicode[STIX]{x1D716}(x)$ is any function tending to 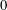$0$ as 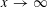$x\rightarrow \infty$, and 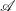$\mathscr{A}$ is a set of integers of cardinality at most 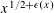$x^{1/2+\unicode[STIX]{x1D716}(x)}$, then the number of integers 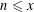$n\leqslant x$ with 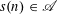$s(n)\in \mathscr{A}$ is 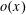$o(x)$, as 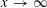$x\rightarrow \infty$. In particular, the EGPS conjecture holds for infinite sets with counting function 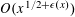$O(x^{1/2+\unicode[STIX]{x1D716}(x)})$. We also disprove a hypothesis from the same paper of EGPS by showing that for any positive numbers $\unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D716}$, there are integers $n$ with arbitrarily many $s$-preimages lying between 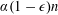$\unicode[STIX]{x1D6FC}(1-\unicode[STIX]{x1D716})n$ and 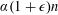$\unicode[STIX]{x1D6FC}(1+\unicode[STIX]{x1D716})n$. Finally, we make some remarks on solutions $n$ to congruences of the form 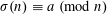$\unicode[STIX]{x1D70E}(n)\equiv a~(\text{mod}~n)$, proposing a modification of a conjecture appearing in recent work of the first two authors. We also improve a previous upper bound for the number of solutions 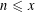$n\leqslant x$, making it uniform in $a$.

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Secondary: 11N64: Other results on the distribution of values or the characterization of arithmetic functions
Type
Research Article
Information
Mathematika , Volume 64 , Issue 2 , 2018 , pp. 330 - 342
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alford, W. R., Granville, A. and Pomerance, C., There are infinitely many Carmichael numbers. Ann. of Math. (2) 139 1994, 703–722.Google Scholar
Anavi, A., Pollack, P. and Pomerance, C., On congruences of the form 𝜎(n) ≡ a (mod n). Int. J. Number Theory 9 2012, 115–124.Google Scholar
Booker, A. R., Finite connected components of the aliquot graph. Math. Comp., doi:10.1090/mcom/3299.Google Scholar
Erdős, P., On the normal number of prime factors of p - 1 and some related problems concerning Euler’s 𝜑-function. Quart. J. Math. (Oxford Ser.) 6 1935, 205–213.Google Scholar
Erdős, P., On integers which are the totient of a product of two primes. Quart. J. Math. (Oxford Ser.) 7 1936, 16–19.CrossRefGoogle Scholar
Erdős, P., Über die Zahlen der Form 𝜎(n) - n und n -𝜑 (n). Elem. Math. 28 1973, 83–86.Google Scholar
Erdős, P., Granville, A., Pomerance, C. and Spiro, C., On the normal behavior of the iterates of some arithmetic functions. In Analytic Number Theory, Proc. Conf. in Honor of Paul T. Bateman (ed. Bateman, P. T. et al. ), Birkhauser (Boston, 1990), 165–204.Google Scholar
Ford, K., The distribution of integers with a divisor in a given interval. Ann. of Math. (2) 168 2008, 367–433.Google Scholar
Hornfeck, B. and Wirsing, E., Über die Häufigkeit vollkommener Zahlen. Math. Ann. 133 1957, 431–438.Google Scholar
Pollack, P., On the greatest common divisor of a number and its sum of divisors. Michigan Math. J. 60 2011, 199–214.CrossRefGoogle Scholar
Pollack, P., Some arithmetic properties of the sum of proper divisors and the sum of prime divisors. Illinois J. Math. 58 2014, 125–147.CrossRefGoogle Scholar
Pollack, P., Palindromic sums of proper divisors. Integers 15A 2015, Paper No. A13, 12 pp.Google Scholar
Pollack, P. and Pomerance, C., Popular values of Euler’s function. Mathematika 27 1980, 84–89.Google Scholar
Pollack, P. and Pomerance, C., Two methods in elementary analytic number theory. In Number Theory and Applications (ed. Mollin, R. A.), Kluwer Academic (Dordrecht, 1989), 135–161.Google Scholar
Pollack, P. and Pomerance, C., On the distribution of some integers related to perfect and amicable numbers. Colloq. Math. 130 2013, 169–182.CrossRefGoogle Scholar
Pollack, P. and Pomerance, C., Some problems of Erdős on the sum-of-divisors function. Trans. Amer. Math. Soc. Ser. B 3 2016, 1–26.Google Scholar
Pollack, P. and Pomerance, C., The first function and its iterates. In Connections in Discrete Mathematics: A Celebration of the Work of Ron Graham (eds Butler, S., Cooper, J. and Hurlbert, G.), Cambridge University Press (Cambridge, 2018).Google Scholar
Pomerance, C., On the congruences 𝜎(n) ≡ a (mod n) and n ≡ a (mod 𝜑(n)). Acta Arith. 26 1975, 265–272.Google Scholar
Prachar, K., Über die Anzahl der Teiler einer natürlichen Zahl, welche die Form p - 1 haben. Monatsh. Math. 59 1955, 91–97.Google Scholar
Troupe, L., On the number of prime factors of values of the sum-of-proper-divisors function. J. Number Theory 150C 2015, 120–135.Google Scholar