Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-05-19T10:46:40.155Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit points of partial sums of Taylor series

Part of: Series expansions

Published online by Cambridge University Press:  26 February 2010

V. Nestoridis
V. Nestoridis
Affiliation:
Department of Mathematics, University of Crete, P. O. Box 1470 Iraklion Crete, Greece.
Get access

Extract

Fifty years ago Marcinkiewicz and Zygmund studied the circular structure of the limit points of the partial sums for (C, 1) summable Taylor series. More specifically, let

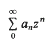
be a power series with complex coefficients, let

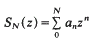
be the partial sums, and let

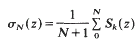
be the Cesàro averages. When the sequence σn(z) converges to a finite limit σ(Z), we say that the Taylor series is (C, 1) summable and σ(z) is the (C, 1) sum of the series. Concerning (C, 1) summable Taylor series Marcinkiewicz and Zygmund ([5], [6] Vol. II, p. 178) established the following theorem.

MSC classification

Secondary: 30B30: Boundary behavior of power series, over-convergence
Type
Research Article
Information
Mathematika , Volume 38 , Issue 2 , December 1991 , pp. 239 - 249
Copyright
Copyright © University College London 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Carleson, L.. On convergence and growth of partial sums of Fourier series. Acta Math., 116 (1966), 135–157.CrossRefGoogle Scholar
2.Kahane, J.-P.. Sur la structure circulaire des ensembles de points limites des sommes partielles d'une serie de Taylor. Acta Sri. Math. (Szeged), 45, 1-4 (1983), 247–251.Google Scholar
3.Katsoprinakis, E.. On a theorem of Marcinkiewicz and Zygmund for Taylor series. Arkiv for Matematik, 27 (1989) 1, 105–126.CrossRefGoogle Scholar
4.Katsoprinakis, E. and Nestoridis, V.. Partial sums of Taylor series on a circle, Ann. Inst. Fourier (Grenoble), 39, 3 (1989), 715–736.CrossRefGoogle Scholar
5.Marcinkiewicz, J. and Zygmund, A.. On the behaviour of trigonometric and power series. T.A.M.S., 50 (1941), 407–453.CrossRefGoogle Scholar
6.Zygmund, A.. Trigonometric series, 2nd edition, reprinted, Vol. I.II (Cambridge: Cambridge University Press, 1968).Google Scholar