Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-28T11:32:58.413Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIPLE EXPONENTIAL AND CHARACTER SUMS WITH MONOMIALS

Part of: Exponential sums and character sums

Published online by Cambridge University Press:  27 May 2014

Igor E. Shparlinski
Igor E. Shparlinski*
Affiliation:
Department of Pure Mathematics, University of New South Wales, Sydney, NSW 2052, Australia email igor.shparlinski@unsw.edu.au
Get access

Abstract

We obtain new bounds of multivariate exponential sums with monomials, when the variables run over rather short intervals. Furthermore, we use the same method to derive estimates on similar sums with multiplicative characters to which previously known methods do not apply. In particular, in the case of multiplicative characters modulo a prime 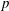$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ we break the barrier of 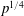$p^{1/4}$ for ranges of individual variables.

MSC classification

Secondary: 11L07: Estimates on exponential sums 11L40: Estimates on character sums
Type
Research Article
Information
Mathematika , Volume 60 , Issue 2 , July 2014 , pp. 363 - 373
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ayyad, A., Cochrane, T. and Zheng, Z., The congruence x 1x 2≡ x 3x 4(mod p), the equation x 1x 2= x 3x 4and the mean value of character sums. J. Number Theory 59 1996, 398–413.CrossRefGoogle Scholar
Bourgain, J., Multilinear exponential sums in prime fields under optimal entropy condition on the sources. Geom. Funct. Anal. 18 2009, 1477–1502.Google Scholar
Bourgain, J., On exponential sums in finite fields. In An Irregular Mind (Bolyai Society Mathematical Studies 21), János Bolyai Math. Soc. (Budapest, 2010), 219–242.CrossRefGoogle Scholar
Bourgain, J. and Chang, M.-C., On a multilinear character sums of Burgess. C. R. Acad. Sci. Paris 348 2010, 115–120.Google Scholar
Bourgain, J. and Garaev, M. Z., On a variant of sum-product estimates and explicit exponential sum bounds in prime fields. Math. Proc. Cambridge Philos. Soc. 146 2008, 1–21.Google Scholar
Bourgain, J. and Garaev, M. Z., Sumsets of reciprocals in prime fields and multilinear Kloosterman sums, Preprint, 2012, arxiv:1211.4184 [math.NT].Google Scholar
Bourgain, J., Garaev, M. Z., Konyagin, S. V. and Shparlinski, I. E., On congruences with products of variables from short intervals and applications. Proc. Steklov Inst. Math. 280 2013, 67–96.Google Scholar
Bourgain, J., Garaev, M. Z., Konyagin, S. V. and Shparlinski, I. E., Multiplicative congruences with variables from short intervals. J. Anal. Math. (to appear).Google Scholar
Davenport, H. and Erdős, P., The distribution of quadratic and higher residues. Publ. Math. Debrecen 2 1952, 252–265.CrossRefGoogle Scholar
Deligne, P., Applications de la formule des traces aux sommes trigonométriques. In Cohomologie Étale (Lecture Notes in Mathematics 569), Springer (Berlin, 1977), 168–232.Google Scholar
Garaev, M. Z., Sums and products of sets and estimates of rational trigonometric sums in fields of prime order. Uspekhi Mat. Nauk. 65 2010, 5–66; Engl. Transl. Russian Math. Surveys 65 (2010), 599–658.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society (Providence, RI, 2004).Google Scholar
Luo, W., Bounds for incomplete hyper-Kloosterman sums. J. Number Theory 75 1999, 41–46.CrossRefGoogle Scholar
Shparlinski, I. E., Bounds of incomplete multiple Kloosterman sums. J. Number Theory 126 2007, 68–73.Google Scholar
Wang, Y. and Li, H., On s-dimensional incomplete Kloosterman sums. J. Number Theory 130 2010, 1602–1608.Google Scholar
Wooley, T. D., Vinogradov’s mean value theorem via efficient congruencing, II. Duke Math. J. 162 2013, 673–730.Google Scholar