Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alon, N.
and
Frankl, P.
1985.
The maximum number of disjoint pairs in a family of subsets.
Graphs and Combinatorics,
Vol. 1,
Issue. 1,
p.
13.
Daykin, David E.
1985.
Graphs and Order.
p.
395.
Alon, Noga
Das, Shagnik
Glebov, Roman
and
Sudakov, Benny
2015.
Comparable pairs in families of sets.
Journal of Combinatorial Theory, Series B,
Vol. 115,
Issue. ,
p.
164.




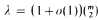 ,
, 