Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-05-19T05:14:33.463Z Has data issue: false hasContentIssue false
  • English
  • Français

ON STABILITY OF SQUARE ROOT DOMAINS FOR NON-SELF-ADJOINT OPERATORS UNDER ADDITIVE PERTURBATIONS

Part of: Elliptic equations and systems General theory of linear operators Groups and semigroups of linear operators, their generalizations and applications Special classes of linear operators Partial differential operators

Published online by Cambridge University Press:  12 March 2015

Fritz Gesztesy ,
Steve Hofmann  and
Roger Nichols
Fritz Gesztesy
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO 65211, U.S.A. email gesztesyf@missouri.edu
Steve Hofmann
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO 65211, U.S.A. email hofmanns@missouri.edu
Roger Nichols
Affiliation:
Mathematics Department, The University of Tennessee at Chattanooga, 415 EMCS Building, Dept. 6956, 615 McCallie Ave, Chattanooga, TN 37403, U.S.A. email Roger-Nichols@utc.edu
Get access

Abstract

Assuming 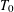$T_{0}$ to be an m-accretive operator in the complex Hilbert space 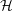${\mathcal{H}}$, we use a resolvent method due to Kato to appropriately define the additive perturbation 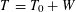$T=T_{0}+W$ and prove stability of square root domains, that is,

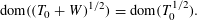$$\begin{eqnarray}\text{dom}((T_{0}+W)^{1/2})=\text{dom}(T_{0}^{1/2}).\end{eqnarray}$$
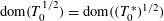Moreover, assuming in addition that $\text{dom}(T_{0}^{1/2})=\text{dom}((T_{0}^{\ast })^{1/2})$, we prove stability of square root domains in the form
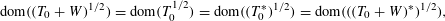$$\begin{eqnarray}\text{dom}((T_{0}+W)^{1/2})=\text{dom}(T_{0}^{1/2})=\text{dom}((T_{0}^{\ast })^{1/2})=\text{dom}(((T_{0}+W)^{\ast })^{1/2}),\end{eqnarray}$$
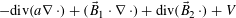 which is most suitable for partial differential equation applications. We apply this approach to elliptic second-order partial differential operators of the form
$$\begin{eqnarray}-\text{div}(a{\rm\nabla}\,\cdot )+(\vec{B}_{1}\cdot {\rm\nabla}\,\cdot )+\text{div}(\vec{B}_{2}\,\cdot )+V\end{eqnarray}$$
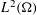 in $L^{2}({\rm\Omega})$ on certain open sets 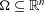${\rm\Omega}\subseteq \mathbb{R}^{n}$, $n\in \mathbb{N}$, with Dirichlet, Neumann, and mixed boundary conditions on 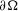$\partial {\rm\Omega}$, under general hypotheses on the (typically, non-smooth, unbounded) coefficients and on 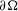$\partial {\rm\Omega}$.

MSC classification

Primary: 35J10: Schrödinger operator 35J25: Boundary value problems for second-order elliptic equations 47A07: Forms (bilinear, sesquilinear, multilinear) 47A55: Perturbation theory
Secondary: 47B44: Accretive operators, dissipative operators, etc. 47D07: Markov semigroups and applications to diffusion processes 47F05: Partial differential operators (should also be assigned at least one other classification number in section 47)
Type
Research Article
Information
Mathematika , Volume 62 , Issue 1 , 2016 , pp. 111 - 182
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, R. and Fournier, J. J. F., Sobolev Spaces, 2nd edn.(Pure and Applied Mathematics 140), Academic Press (New York, 2003).Google Scholar
Albrecht, D., Duong, X. and McIntosh, A., Operator theory and harmonic analysis. In Workshop in Analysis and Geometry, 1995 (CMA Proceedings 34) (eds Cranny, T. R. and Hutchinson, J. E.), Australian National University (Canberra, 1996), 77–136.Google Scholar
Alexopoulos, G., La conjecture de Kato pour des opérateurs différentiels elliptiques, à coefficients périodiques. C. R. Acad. Sci. Paris Ser. I 312 1991, 263–266.Google Scholar
Alfonseca, M., Auscher, P., Axelsson, A., Hofmann, S. and Kim, S., Analyticity of layer potentials and L 2 solvability of boundary value problems for divergence form elliptic equations with complex L ∞ coefficients. Adv. Math. 226 2011, 4533–4606.CrossRefGoogle Scholar
Arendt, W. and ter Elst, A. F. M., Gaussian estimates for second order elliptic operators with boundary conditions. J. Operator Theory 38 1997, 87–130.Google Scholar
Assaad, J. and Ouhabaz, E. M., Riesz transforms of Schrödinger operators on manifolds. J. Geom. Anal. 22 2012, 1108–1126.CrossRefGoogle Scholar
Auscher, P., Lectures on the Kato square root problem. In Surveys in Analysis and Operator Theory, ANU, 2001–2002 (CMA Proceedings 40) (ed. Hassell, A.), Australian National University (Canberra, 2002), 1–18.Google Scholar
Auscher, P., On L p estimates for square roots of second order elliptic operators on ℝn. Publ. Mat. 48 2004, 159–186.CrossRefGoogle Scholar
Auscher, P., On necessary and sufficient conditions for L p-estimates of Riesz transforms associated with elliptic operators on ℝn and related estimates. Mem. Amer. Math. Soc. 186(871) 2007.Google Scholar
Auscher, P., Axelsson, A. and McIntosh, A., On a quadratic estimate related to the Kato conjecture and boundary value problems. In Harmonic Analysis and Partial Differential Equations (Contemporary Mathematics 505) (eds Cifuentes, P., Garcia-Cuerva, J., Garrigós, G., Hernández, E., Martell, J. M., Parcet, J., Ruiz, A., Soria, F., Torrea, J. L. and Vargas, A.), American Mathematical Society (Providence, RI, 2001), 105–129.Google Scholar
Auscher, P., Axelsson, A. and McIntosh, A., Solvability of elliptic systems with square integrable boundary data. Ark. Mat. 48 2010, 253–287.CrossRefGoogle Scholar
Auscher, P., Badr, N., Haller-Dintelmann, R. and Rehberg, J., The square root problem for second order, divergence form operators with mixed boundary conditions on $L^{p}$. Preprint, 2012,arXiv:1210.0780.Google Scholar
Auscher, P., Hofmann, S., Lacey, M., Lewis, J., McIntosh, A. and Tchamitchian, Ph., The solution of Kato’s conjecture. C. R. Acad. Sci. Paris I 332 2001, 601–606.CrossRefGoogle Scholar
Auscher, P., Hofmann, S., Lacey, M., McIntosh, A. and Tchamitchian, Ph., The solution of the Kato square root problem for second order elliptic operators on ℝn. Ann. of Math. (2) 156 2002, 633–654.CrossRefGoogle Scholar
Auscher, P., Hofmann, S., Lewis, J. L. and Tchamitchian, Ph., Extrapolation of Carleson measures and the analyticity of Kato’s square root operators. Acta Math. 187 2001, 161–190.CrossRefGoogle Scholar
Auscher, P., Hofmann, S., McIntosh, A. and Tchamitchian, Ph., The Kato square root problem for higher order elliptic operators and systems on ℝn. J. Evol. Equ. 1 2001, 361–385.CrossRefGoogle Scholar
Auscher, P., McIntosh, A. and Nahmod, A., Holomorphic functional calculi of operators, quadratic estimates and interpolation. Indiana Univ. Math. J. 46 1997, 375–403.CrossRefGoogle Scholar
Auscher, P., McIntosh, A. and Nahmod, A., The square root problem of Kato in one dimension, and first order elliptic systems. Indiana Univ. Math. J. 46 1997, 659–695.CrossRefGoogle Scholar
Auscher, P., McIntosh, A. and Tchamitchian, Ph., Heat kernel of complex elliptic operators and applications. J. Funct. Anal. 152 1998, 22–73.CrossRefGoogle Scholar
Auscher, P. and Russ, E., Hardy spaces and divergence operators on strongly Lipschitz domains of ℝn. J. Funct. Anal. 201 2003, 148–184.CrossRefGoogle Scholar
Auscher, P. and Tchamitchian, Ph., Ondelettes et conjecture de Kato. C. R. Acad. Sci. Paris I 313 1991, 63–66.Google Scholar
Auscher, P. and Tchamitchian, Ph., Conjecture de Kato sur les ouverts de ℝ. Rev. Mat. Iberoam. 8 1992, 149–199.CrossRefGoogle Scholar
Auscher, P. and Tchamitchian, Ph., Square root problem for divergence operators, square functions, and singular integrals. Math. Res. Lett. 3 1996, 429–437.CrossRefGoogle Scholar
Auscher, P. and Tchamitchian, Ph., Square Root Problem for Divergence Operators and Related Topics (Astérisque 249), Société Mathématique de France (1998).Google Scholar
Auscher, P. and Tchamitchian, Ph., Square roots of elliptic second order divergence operators on strongly Lipschitz domains: L p theory. Math. Ann. 320 2001, 577–623.CrossRefGoogle Scholar
Auscher, P. and Tchamitchian, Ph., Square roots of elliptic second order divergence operators on strongly Lipschitz domains: L 2 theory. J. Anal. Math. 90 2003, 1–12.CrossRefGoogle Scholar
Axelsson, A., Keith, S. and McIntosh, A., The Kato square root problem for mixed boundary value problems. J. Lond. Math. Soc. (2) 74 2006, 113–130.CrossRefGoogle Scholar
Bandara, L., ter Elst, A. F. M. and McIntosh, A., Square roots of perturbed subelliptic operators on Lie groups. Stud. Math. 216 2013, 193–217.CrossRefGoogle Scholar
Coifman, R. R., Lions, P.-L., Meyer, Y. and Semmes, S., Compacité par compensation et espaces de Hardy. C. R. Acad. Sci. Paris 309 1989, 945–949.Google Scholar
Coifman, R. R., McIntosh, A. and Meyer, Y., L’intégrale de Cauchy définit un opérateur borné sur L 2 pour les courbes lipschitziennes. Ann. of Math. (2) 116 1982, 361–387.CrossRefGoogle Scholar
Coifman, R. and Meyer, Y., Non-linear harmonic analysis and PDE. In Beijing Lectures in Harmonic Analysis (Annals of Mathematical Studies 112) (ed. Stein, E. M.), Princeton University Press (Princeton, NJ, 1986).Google Scholar
Cruz-Uribe, D. and Rios, C., The solution of the Kato problem for degenerate elliptic operators with Gaussian bounds. Trans. Amer. Math. Soc. 364 2012, 3449–3478.CrossRefGoogle Scholar
Dautray, R. and Lions, J.-L., Mathematical Analysis and Numerical Methods for Science and Technology, Vol. 2, Functional and Variational Methods, Springer (Berlin, 2000).Google Scholar
Davies, E. B., Heat Kernels and Spectral Theory (Cambridge Tracts in Mathematics 92), Cambridge University Press (Cambridge, 1989).CrossRefGoogle Scholar
Edmunds, D. E. and Evans, W. D., Spectral Theory and Differential Operators, Clarendon Press (Oxford, 1989).Google Scholar
ter Elst, A. F. M. and Robinson, D. W., On Kato’s square root problem. Hokkaido Math. J. 26 1997, 365–376.Google Scholar
Faris, W. G., Quadratic forms and essential self-adjointness. Helv. Phys. Acta 45 1972, 1074–1088.Google Scholar
Faris, W. G., Self-Adjoint Operators (Lecture Notes in Mathematics 433), Springer (Berlin, 1975).CrossRefGoogle Scholar
Fefferman, C. and Stein, E. M., H p spaces of several variables. Acta Math. 129 1972, 137–193.CrossRefGoogle Scholar
Ford, R. L., Generalized potentials and obstacle scattering. Trans. Amer. Math. Soc. 329 1992, 415–431.CrossRefGoogle Scholar
Fujiwara, D., Concrete characterization of the domains of fractional powers of some elliptic differential operators of the second order. Proc. Japan Acad. 43 1967, 82–86.Google Scholar
Gesztesy, F., Hofmann, S. and Nichols, R., Stability of square root domains for one-dimensional non-self-adjoint 2nd-order linear differential operators. Methods Funct. Anal. Topology 19 2013, 227–259 (for corrections, see Methods Funct. Anal. Topology 21(1) (2015) and arXiv:1305.2650).Google Scholar
Gesztesy, F., Hofmann, S. and Nichols, R., Stability of square root domains associated with elliptic systems of PDEs on nonsmooth domains. J. Differential Equations 258 2015, 1749–1764.CrossRefGoogle Scholar
Gesztesy, F., Latushkin, Y., Mitrea, M. and Zinchenko, M., Nonselfadjoint operators, infinite determinants, and some applications. Russ. J. Math. Phys. 12 2005, 443–471.Google Scholar
Gesztesy, F. and Mitrea, M., Nonlocal Robin Laplacians and some remarks on a paper by Filonov on eigenvalue inequalities. J. Differential Equations 247 2009, 2871–2896.CrossRefGoogle Scholar
Gesztesy, F. and Zinchenko, M., Symmetrized perturbation determinants and applications to boundary data maps and Krein-type resolvent formulas. Proc. Lond. Math. Soc. (3) 104 2012, 577–612.CrossRefGoogle Scholar
Griepentrog, J. A., Gröger, K., Kaiser, H.-C. and Rehberg, J., Interpolation for function spaces related to mixed boundary value problems. Math. Nachr. 241 2002, 110–120.3.0.CO;2-R>CrossRefGoogle Scholar
Griepentrog, J. A., Kaiser, H.-C. and Rehberg, J., Heat kernel and resolvent properties for second order elliptic differential operators with general boundary conditions on L p. Adv. Math. Sci. Appl. 11 2001, 87–112.Google Scholar
Gröger, K., A W 1, p-estimate for solutions to mixed boundary value problems for second order elliptic differential equations. Math. Ann. 283 1989, 679–687.CrossRefGoogle Scholar
Gröger, K. and Rehberg, J., Resolvent estimates in W −1, p for second order elliptic differential operators in case of mixed boundary conditions. Math. Ann. 285 1989, 105–113.CrossRefGoogle Scholar
Gurarie, D., On L p-domains of fractional powers of singular elliptic operators and Kato’s conjecture. J. Operator Theory 27 1992, 193–203.Google Scholar
Haase, M., The Functional Calculus for Sectorial Operators (Operator Theory: Advances and Applications 169), Birkhäuser (Basel, 2006).CrossRefGoogle Scholar
Haller-Dintelmann, R., Hieber, M. and Rehberg, J., Irreducibility and mixed boundary conditions. Positivity 12 2008, 83–91.CrossRefGoogle Scholar
Haller-Dintelmann, R., Meyer, C., Rehberg, J. and Schiela, A., Hölder continuity and optimal control for nonsmooth elliptic problems. Appl. Math. Optim. 60 2009, 397–428.CrossRefGoogle Scholar
Haller-Dintelmann, R. and Rehberg, J., Mixed parabolic regularity for divergence operators including mixed boundary conditions. J. Differential Equations 247 2009, 1354–1396.CrossRefGoogle Scholar
Hofmann, S., The solution of the Kato problem. In Harmonic Analysis and Boundary Value Problems (Fayetteville, AR, 2000) (Contemporary Mathematics 277) (eds Capogna, L. and Lanzani, L.), American Mathematical Society (Providence, RI, 2001), 39–43.CrossRefGoogle Scholar
Hofmann, S., A short course on the Kato problem. In Second Summer School in Analysis and Mathematical Physics: Topics in Analysis: Harmonic, Complex, Nonlinear and Quantization (Cuernavaca, 2000) (Contemporary Mathematics 289) (eds Pérez-Esteva, S. and Villegas-Blas, C.), American Mathematical Society (Providence, RI, 2001), 61–77.Google Scholar
Hofmann, S., Lacey, M. and McIntosh, A., The solution of the Kato problem for divergence form elliptic operators with Gaussian heat kernel bounds. Ann. of Math. (2) 156 2002, 623–631.CrossRefGoogle Scholar
Hofmann, S. and Martell, J. M., L p bounds for Riesz transforms and square roots associated to second order elliptic operators. Publ. Mat. 47(2) 2003, 497–515.CrossRefGoogle Scholar
Hofmann, S. and McIntosh, A., The solution of the Kato problem in two dimensions. Proc. Conf. Harmonic Analysis and PDE (El Escorial, Spain, July 2000), Publ. Mat. extra volume 2002, 143–160.Google Scholar
Hoke, K., Kaiser, H.-C. and Rehberg, J., Analyticity for some operator functions from statistical quantum mechanics. Ann. Henri Poincaré 10 2009, 749–771.CrossRefGoogle Scholar
Hytönen, T., McIntosh, A. and Portal, P., Kato’s square root problem in Banach spaces. J. Funct. Anal. 254 2008, 675–726.CrossRefGoogle Scholar
Journé, J.-L., Remarks on Kato’s square root problem. Publ. Mat. 35 1991, 299–321.CrossRefGoogle Scholar
Kaiser, H.-C. and Rehberg, J., On stationary Schrödinger–Poisson equations modelling an electron gas with reduced dimension. Math. Methods Appl. Sci. 20 1997, 1283–1312.3.0.CO;2-P>CrossRefGoogle Scholar
Kaiser, H.-C. and Rehberg, J., About a one-dimensional stationary Schrödinger–Poisson system with a Kohn–Sham potential. Z. Angew. Math. Phys. 50 1999, 423–458.CrossRefGoogle Scholar
Kaiser, H.-C. and Rehberg, J., About a stationary Schrödinger–Poisson system with a Kohn–Sham potential in a bounded two- and three-dimensional domain. Nonlinear Anal. 41 2000, 33–72.CrossRefGoogle Scholar
Kato, T., Fractional powers of dissipative operators. J. Math. Soc. Japan 13 1961, 246–274.CrossRefGoogle Scholar
Kato, T., Fractional powers of dissipative operators, II. J. Math. Soc. Japan 14 1962, 242–248.CrossRefGoogle Scholar
Kato, T., Wave operators and similarity for some non-selfadjoint operators. Math. Ann. 162 1966, 258–279.CrossRefGoogle Scholar
Kato, T., Perturbation Theory for Linear Operators, corrected printing of the 2nd edn., Springer (Berlin, 1980).Google Scholar
Kenig, C. and Meyer, Y., Kato’s square roots of accretive operators and Cauchy kernels on Lipschitz curves are the same. In Recent Progress in Fourier Analysis (eds Peral, I. and Rubio de Francia, J.-L.), Elsevier–North-Holland (Amsterdam, 1985).Google Scholar
Kunstmann, P. C. and Weis, L., Maximal L p -regularity for parabolic equations, Fourier multiplier theorems and H ∞-functional calculus. In Functional Analytic Methods for Evolution Equations (Lecture Notes in Mathematics 1855) (eds Iannelli, M., Nagel, R. and Piazzera, S.), Springer (Berlin, 2004), 65–311.CrossRefGoogle Scholar
Lions, J. L., Espaces d’interpolation et domaines de puissances fractionnaires d’opérateurs. J. Math. Soc. Japan 14 1962, 233–241.CrossRefGoogle Scholar
McIntosh, A., Bilinear forms in Hilbert space. J. Math. Mech. 19 1970, 1027–1045.Google Scholar
McIntosh, A., On the comparability of A 1∕2 and A ∗1∕2. Proc. Amer. Math. Soc. 32 1972, 430–434.Google Scholar
McIntosh, A., On representing closed accretive sesquilinear forms as (A 1∕2u, A ∗1∕2v). In Nonlinear Partial Differential Equations and their Applications (Collège de France Seminar III) (eds Brezis, H. and Lions, J. L.), Pitman (Boston, MA, 1982), 252–267. D. Cioranescu (coordinator).Google Scholar
McIntosh, A., Square roots of elliptic operators. J. Funct. Anal. 61 1985, 307–327.CrossRefGoogle Scholar
McIntosh, A., Operators which have an H ∞ functional calculus. In Miniconference on Operator Theory and Partial Differential Equations, Macquarie University, 1986 (CMA Proceedings 14) (eds Jefferies, B., McIntosh, A. and Ricker, W.), Australian National University (Canberra, 1986), 210–231.Google Scholar
McIntosh, A., The square root problem for elliptic operators. A survey. In Functional–Analytic Methods for Partial Differential Equations (Lecture Notes in Mathematics 1450), Springer (Berlin, 1990), 122–140.CrossRefGoogle Scholar
Miyazaki, Y., Domains of square roots of regularly accretive operators. Proc. Japan Acad. A 67 1991, 38–42.CrossRefGoogle Scholar
Morris, A., The Kato square root problem on submanifolds. J. Lond. Math. Soc. (2) 86 2012, 879–910.CrossRefGoogle Scholar
Ouhabaz, E. M., Gaussian upper bounds for heat kernels of second-order elliptic operators with complex coefficients on arbitrary domains. J. Operator Theory 51 2004, 335–360.Google Scholar
Ouhabaz, E. M., Analysis of Heat Equations on Domains (London Mathematical Society Monographs Series 31), Princeton University Press (Princeton, NJ, 2005).Google Scholar
Reed, M. and Simon, B., Methods of Modern Mathematical Physics. III: Scattering Theory, Academic Press (New York, 1979).Google Scholar
Schechter, M., Hamiltonians for singular potentials. Indiana Univ. Math. J. 22 1972, 483–503.CrossRefGoogle Scholar
Simon, B., Quantum Mechanics for Hamiltonians Defined as Quadratic Forms, Princeton University Press (Princeton, NJ, 1971).Google Scholar
Simon, B., Trace Ideals and their Applications, 2nd edn.(Mathematical Surveys and Monographs 120), American Mathematical Society (Providence, RI, 2005).Google Scholar
Stein, E. M., Singular Integrals and Differentiability Properties of Functions, Princeton University Press (Princeton, NJ, 1970).Google Scholar
Stollmann, P. and Voigt, J., A regular potential which is nowhere in L 1. Lett. Math. Phys. 9 1985, 227–230.CrossRefGoogle Scholar
Yagi, A., Coïncidence entre des espaces d’interpolation et des domaines de puissances fractionnaires d’opérateurs. C. R. Acad. Sci. Paris Ser. I 299 1984, 173–176.Google Scholar
Yagi, A., Applications of the purely imaginary powers of operators in Hilbert spaces. J. Funct. Anal. 73 1987, 216–231.CrossRefGoogle Scholar
Yagi, A., Abstract Parabolic Evolution Equations and their Applications, Springer (Berlin, 2010).CrossRefGoogle Scholar