Article contents
ON THE METRIC THEORY OF CONTINUED FRACTIONS IN POSITIVE CHARACTERISTIC
Published online by Cambridge University Press: 27 May 2014
Abstract
Let 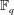 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_q$ be the finite field of
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{F}_q$ be the finite field of 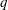 $q$ elements. An analogue of the regular continued fraction expansion for an element
$q$ elements. An analogue of the regular continued fraction expansion for an element  $\alpha $ in the field of formal Laurent series over
$\alpha $ in the field of formal Laurent series over 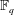 $\mathbb{F}_q$ is given uniquely by
$\mathbb{F}_q$ is given uniquely by 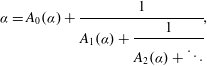 $$\begin{equation*} \alpha = A_0(\alpha )+\cfrac {1}{A_1(\alpha )+\cfrac {1}{A_2(\alpha )+\ddots }}, \end{equation*}$$
$$\begin{equation*} \alpha = A_0(\alpha )+\cfrac {1}{A_1(\alpha )+\cfrac {1}{A_2(\alpha )+\ddots }}, \end{equation*}$$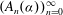 $(A_n(\alpha ))_{n=0}^\infty $ is a sequence of polynomials with coefficients in
$(A_n(\alpha ))_{n=0}^\infty $ is a sequence of polynomials with coefficients in 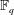 $\mathbb{F}_q$ such that
$\mathbb{F}_q$ such that 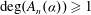 $\deg (A_n(\alpha ))\ge 1$ for all
$\deg (A_n(\alpha ))\ge 1$ for all 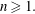 $n\ge 1.$ We first prove the exactness of the continued fraction map in positive characteristic. This fact implies a number of strictly weaker properties. Particularly, we then use the weak-mixing property and ergodicity to establish various metrical results regarding the averages of partial quotients of continued fraction expansions. A sample result that we prove is that if
$n\ge 1.$ We first prove the exactness of the continued fraction map in positive characteristic. This fact implies a number of strictly weaker properties. Particularly, we then use the weak-mixing property and ergodicity to establish various metrical results regarding the averages of partial quotients of continued fraction expansions. A sample result that we prove is that if 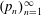 $(p_n)_{n=1}^\infty $ denotes the sequence of prime numbers, we have
$(p_n)_{n=1}^\infty $ denotes the sequence of prime numbers, we have 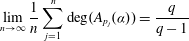 $$\begin{equation*} \lim _{n\to \infty }\frac {1}{n}\sum _{j=1}^n \deg (A_{p_j}(\alpha )) = \frac {q}{q-1} \end{equation*}$$
$$\begin{equation*} \lim _{n\to \infty }\frac {1}{n}\sum _{j=1}^n \deg (A_{p_j}(\alpha )) = \frac {q}{q-1} \end{equation*}$$ $\alpha $ with respect to Haar measure. In the case where the sequence
$\alpha $ with respect to Haar measure. In the case where the sequence 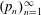 $(p_n)_{n=1}^\infty $ is replaced by
$(p_n)_{n=1}^\infty $ is replaced by 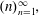 $(n)_{n=1}^\infty ,$ this result is due to V. Houndonougbo, V. Berthé and H. Nakada. Our proofs rely on pointwise subsequence and moving average ergodic theorems.
$(n)_{n=1}^\infty ,$ this result is due to V. Houndonougbo, V. Berthé and H. Nakada. Our proofs rely on pointwise subsequence and moving average ergodic theorems.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2014
References
- 2
- Cited by




