Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-05-28T03:15:36.059Z Has data issue: false hasContentIssue false
  • English
  • Français

On the scarcity of powerful binomial coefficients

Part of: Sequences and sets

Published online by Cambridge University Press:  26 February 2010

Andrew Granville
Andrew Granville
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA 30602, U.S.A. E-mail: andrew@math.uga.edu
Get access

Abstract

Assuming the abc-conjecture, it is shown that there are only finitely many powerful binomial coefficients 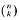with 3≤k≤n/2 in fact, if q2 divides 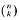, then 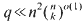. Unconditionally, it is shown that there are N1/2+σ(1) powerful binomial coefficients in the top N rows of Pascal's Triangle.

MSC classification

Secondary: 11B65: Binomial coefficients; factorials; $q$-identities
Type
Research Article
Information
Mathematika , Volume 46 , Issue 2 , December 1999 , pp. 397 - 410
Copyright
Copyright © University College London 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Mile, A. D. Nouv. Ann. Math., 16 (1857), 288–290.Google Scholar
2. Cohen, H. and Lenstra, H. W. Jr. Heuristics on class groups of number fields. Lecture Notes in Math., 1068 (1984), 33–62.CrossRefGoogle Scholar
3. Davenport, H.. Multiplicative Number Theory, vol. 2nd ed., (Springer-Verlag, New York. 1980).CrossRefGoogle Scholar
4. Erdős, P.. On a Diophantine Equation. J. London Math. Soc, 26 (1951), 176–178.CrossRefGoogle Scholar
5. Erdős, P. and Graham, R. L.. Old and new problems and results in combinatorial number theory. L'Enseign. Math., Geneva, 1980.Google Scholar
6. Erdős, P. and Selfridge, J. L.. The product of consecutive integers is never a power. Illinois J. Math., 19 (1975), 292–301.CrossRefGoogle Scholar
7. Goldbach, C.. letter to D. Bernoulli (July 23rd, 1724).Google Scholar
8. Granville, A. and Ramare, O.. Explicit bounds on exponential sums and the scarcity of squarefree binomial coefficients. Mathematika, 43 (1996), 73–107.CrossRefGoogle Scholar
9. Guy, R. K., Unsolved Problems in Number Theory, vol. 2nd ed., (Springer-Verlag, New York. 1994).Google Scholar
10. Langevin, M.. Cas déégalite pour le Théorème de Mason et applications de la conjecture (abc). C. R. Acad. Sci. Paris, 317 (1993), 441–444.Google Scholar
11. Sander, J. W.. Prime power divisors of binomial coefficients. J. reine angew Math., 430 (1992), 1–20.Google Scholar
12. Shiu, P.. On the number of square-full integers between successive squares. Mathematika. 27 (1980), 171–178.CrossRefGoogle Scholar